자연수 거듭제곱의 합

자연수의 합

먼저 자연수의 합은 등차수열 합으로 간단히 적을 수 있다. 이를 그림으로 나타내면 아래와 같다.

$$\sum _{k=1} ^{n} k =1 +2 +3 + \cdots +n = \frac{1}{2}n(n+1)$$

$\bullet$                                      $\overbrace{\bullet \bullet \bullet \bullet \cdots \cdots \bullet}^{n}$

$\bullet \bullet$                                          $\overbrace{\bullet \bullet \bullet \bullet \cdots \bullet}^{n-1}$

$\bullet \bullet \bullet$                     $+$                 $\overbrace{\bullet \bullet \bullet \cdots \bullet}^{n-2}$

  
  $\vdots$                                              $\vdots$ 

$\underbrace{\bullet \bullet \bullet \bullet \cdots \bullet}_{n-1}$                                       $\bullet \bullet$

$\underbrace{\bullet \bullet \bullet \bullet \cdots \cdots \bullet}_{n}$                                      $\bullet$

$$\sum_{k=1}^{n}k +\sum_{k=1}^{n}k=n(n+1)$$

거듭제곱의 합

자연수 거듭제곱을 더한 공식을 증명하는 방법은 여러 가지가 있다. 여기서는 보통 교과서와 있는 항등식을 이용한 방법과 다른 방식으로 증명하고자 한다.

 $$\sum _{k=1} ^{n} k^2 =1^2 +2^2 +3^2 + \cdots +n^2 = \frac{1}{6}n(n+1)(2n+1)$$

증명) 공식을 뜯어보면 자연수의 합과 관련이 있다는 걸 알 수 있다.

먼저 $n=4$일 때, 자연수 제곱의 합을 다르게 적어보면 아래와 같다.

$$ \sum_{k=1}^{4}k^2 =1^2 +2^2 +3^2 +4^2 =1+(2+2)+(3+3+3)+(4+4+4+4)$$

이를 아래와 같이 적어보자.

$$\begin{split}&1&\quad\quad\quad\quad&4&\quad\quad\quad\quad&4&\quad\quad\quad\quad&9&\quad\\&22&\quad\quad&34&\quad\quad&43&&99&\\&333&\quad+\quad&234&\quad+\quad&432&\quad=\quad&999&\\&4444&\quad&1234&\quad&4321&\quad&9999&\end{split}$$

삼각형 모양에서 같은 자리에 있는 수를 더한 값이 모두 같음을 알 수 있다. 따라서

$$\sum_{k=1}^{4}k^2 +\sum_{k=1}^{4}k^2 +\sum_{k=1}^{4}k^2 =9(1+2+3+4)$$

이를 일반화 해보면 아래와 같다.

$$\sum_{k=1}^{n}k^2 +\sum_{k=1}^{n}k^2 +\sum_{k=1}^{n}k^2 =(2n+1)(1+2+3+4+\cdots +n)$$

$$3\sum_{k=1}^{n}k^2 =(2n+1)\sum_{k=1}^{n}k$$

$$3\sum_{k=1}^{n}k^2 =\frac{1}{2}n(n+1)(2n+1)$$

$$\therefore \sum_{k=1}^{n}k^2 =\frac{1}{6}n(n+1)(2n+1)$$

$\blacksquare$

세제곱의 합

사각수 그림이다.

\begin{split}1\\1+2+1=2^2\\1+2+3+2+1=3^2\\1+2+3+4+3+2+1=4^2\end{split}

$$1+2+3+\cdots+(n-1)+n+(n-1)+\cdots+3+2+1=n^2$$

아래 그림을 참고하여 자연수 세제곱의 합을 알아보자.

$$\begin{split}\sum_{k=1}^{4} k^3 &=1^3 +2^3 +3^3 +4^3\\&=1+2(1+2+1)+3(1+2+3+2+1)+4(1+2+3+4+3+2+1) \\&=1+(2+4+2)+(3+6+9+6+3)+(4+8+12+16+12+8+4)\end{split}$$

 

그림과 같이 더하는 순서를 다시 배열하면 오른쪽에 있는 식을 모두 더한 것과 같다.

$$\begin{split}(1+2+3+4)+2(1+2+3+4)+3(1+2+3+4)+4(1+2+3+4)\\=(1+2+3+4)(1+2+3+4)\end{split}$$

$$\therefore \sum_{k=1}^{4} k^3 =(1+2+3+4)^2 =\bigg( \sum_{k=1}^{4} k \bigg)^2$$이다.

자연수 세제곱의 합은 이를 일반화하면 된다.

$$\sum_{k=1}^{n} k^3 = \bigg( \sum_{k=1}^{n} k \bigg)^2 = \bigg( \frac{1}{2} n(n+1) \bigg)^2$$

그림으로 보이면 아래와 같다.

 

$$1^3 +2^3+3^3+\cdots+n^3 =(1+2+3+\cdot+n)^2$$

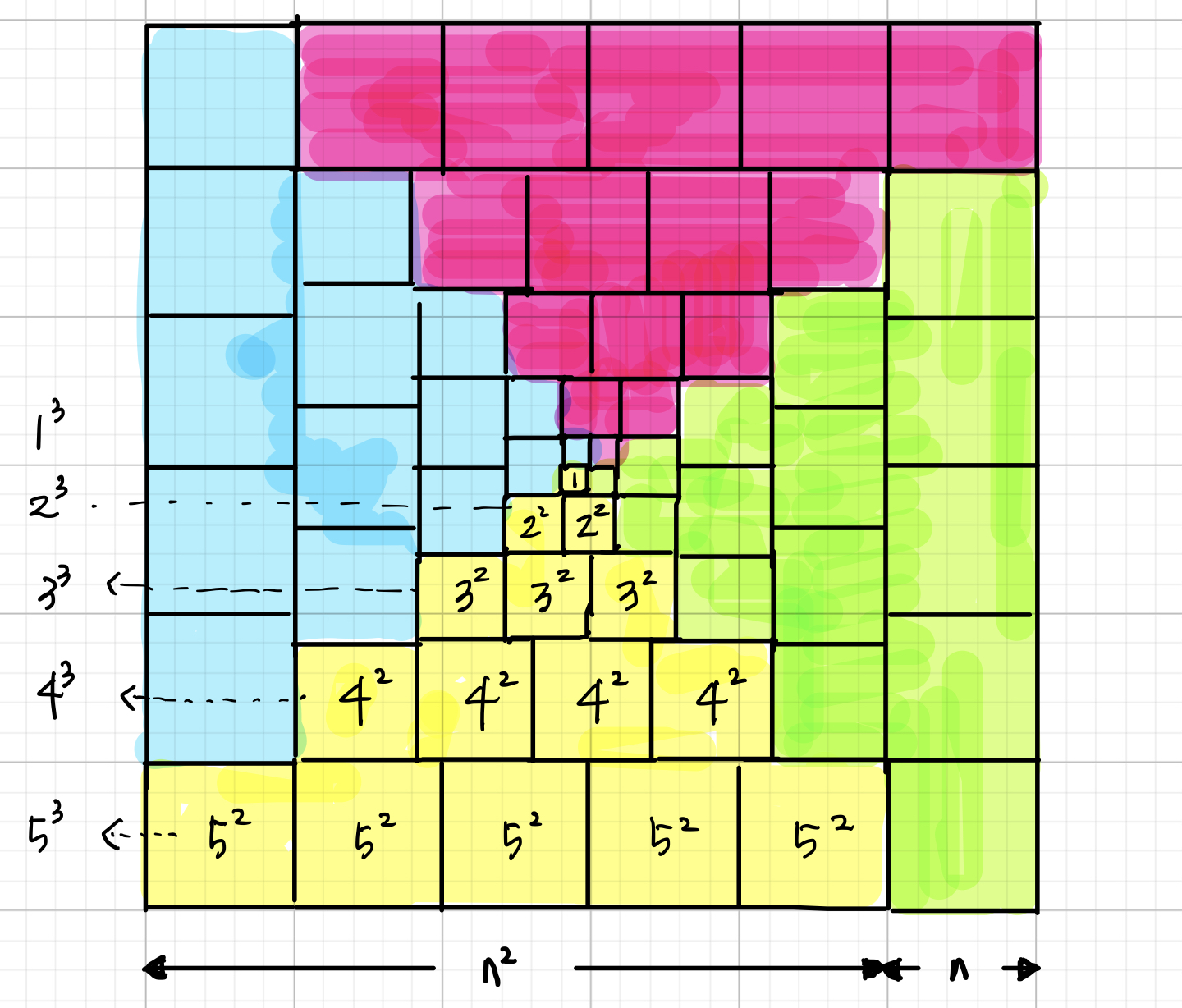
$$4(1^3 +2^3+3^3+\cdots+n^3 )=(n^2+n)^2$$

$$1^3 +2^3+3^3+\cdots+n^3 =\frac{1}{4}n^2(n+1)^2=\left(\frac{1}{2}n(n+1)\right)^2$$

거듭제곱의 합 2

세제곱의 합을 알면 다시 제곱의 합을 아래와 같이 보일 수 있다.

$$\begin{align}\sum_{k=1}^{n}k^2 &=\left(\sum_{k=1}^{n}k \right)^2- 2\sum_{k=1}^{n-1}\left[ \left(\sum_{i=1}^{k}i\right)(k+1)\right] \\&=\left(\sum_{k=1}^{n}k \right)^2-2\sum_{k=1}^{n-1}\frac{1}{2}k(k+1)(k+1)\\ &=\left(\sum_{k=1}^{n}k \right)^2-\sum_{k=1}^{n-1}(k^3 +2k^2+k)\\ &=\left(\sum_{k=1}^{n}k \right)^2-\sum_{k=1}^{n}(k^3 +2k^2+k)+n^3 +2n^2+n\\&=-2\sum_{k=1}^{n}k^2-\sum_{k=1}^{n}k+n^3+2n^2+n \end{align}$$

$$\begin{split}3\sum_{k=1}^{n}k^2&=-\frac{1}{2}n^2-\frac{1}{2}n+n^3+2n^2+n\\&=\frac{1}{2}n(2n^2+3n+n)\\&=\frac{1}{2}n(n+1)(2n+1)\end{split}$$