과학고 심화수학1 종합문제 p202풀이
수학이야기/기하벡터 2017. 4. 12. 17:57
1. 한 원과 포물선은 교점을 $0,1,2,3,4$개 가질 수 있다. 주어진 원 $x^2 +y^2 =4$과 포물선 $y=x^2 +C$의 교점의 개수를 $C$에 따라 분류하여라.
풀이 그림을 그려서 접하는 경우를 찾아서 해결하면 되므로 따로 적지 않는다.
2. 포물선 위의 점을 중심으로 하고 초점을 지나는 현을 지름으로 하는 원은 그 포물선의 준선에 접합을 보여라.
풀이 포물선 정의에 따라 쉽게 해결할 수 있으므로 따로 적지 않는다.
3. 포물선 $y^2 = 2x$의 초점 $F$를 지나고 그 끝점이 포물선 위에 있는 두 선분 $\overline{AB},\overline{CD}$가 서로 직교하고 있다. 이 때
$$\frac{1}{\overline{AF}\cdot \overline{BF}}+\frac{1}{\overline{CF}\cdot \overline{CF}}$$의 값을 구하여라.
먼저 초점 $F(1/2,0)$를 지나고 서로 수직인 직선$\overline{AB},\overline{CD}$을 각각
$$y=m\bigg(x-\frac{1}{2}\bigg),\;\;y=-\frac{1}{m}\bigg(x-\frac{1}{2}\bigg)$$
라고 하자.
직선 $\displaystyle{y=m\bigg(x-\frac{1}{2}\bigg)}$와 포물선이 만나는 점을 $A(x_1,y_1), B(x_2,y_2)$라고 하면
$\displaystyle{\frac{y}{m}=x-\frac{1}{2}}$이고 $\displaystyle{x=\frac{y}{m}+\frac{1}{2}}$을 포물선 방정식에 넣어서 정리한 이차방정식
$$y^2-\frac{2}{m}y-1=0$$의 두 근이 $y_1, y_2$이다. 따라서 $y_1 y_2=-1$이다.
$$\overline{AF}\cdot \overline{BF}=\sqrt{\bigg(x_1 -\frac{1}{2}\bigg)^2+y_1^2}\sqrt{\bigg(x_2 -\frac{1}{2}\bigg)^2+y_2^2}=\sqrt{\bigg(\frac{y_1}{m}\bigg)^2+y_1^2}\sqrt{\bigg(\frac{y_2}{m}\bigg)^2+y_2^2}$$
$$\therefore \overline{AF}\cdot \overline{BF}=|y_1 y_2|\bigg(\frac{1}{m^2}+1\bigg)=\frac{m^2+1}{m^2}$$
마찬가지로 $\displaystyle{y=-\frac{1}{m}\bigg(x-\frac{1}{2}\bigg)}$와 포물선이 만나는 점을 $C(x_3,y_3), D(x_4,y_4)$라고 하면
$$y^2+2my-1=0$$의 두 근이 $y_3, y_4$이고 $y_3 y_4=-1$이다. 같은 방법으로
$$\therefore \overline{CF}\cdot \overline{DF}=|y_1 y_2|(m^2+1)=m^2+1$$
주어진 식을 정리하면
$$\frac{1}{\overline{AF}\cdot \overline{BF}}+\frac{1}{\overline{CF}\cdot \overline{CF}}=\frac{m^2}{m^2+1}+\frac{1}{m^2+1}=1$$
더 일반적인 기하적 증명은 주어진 그림과 13번 풀이를 참고하여 구해도 된다.
4. 그림과 같이 포물선 $y^2 =4x$에 내접하는 사다리꼴 $ABCD$가 주어져 있다. 이 때 $\overline{AB}+\overline{BC}+\overline{CD}+\overline{DA}$의 최솟값을 구하여라.
포물선 정의에 따라 $\overline{BF}+\overline{BA}=\overline{CF}+\overline{CD}=4$로 일정하다. 따라서 $\overline{AD}$가 최소일 때를 생각하면 된다. $(1.0)$을 지나는 직선을 $my+1=x$라고 하자. $$y^2=4my+4$$이므로 교점의 $y$좌표를 각각 $y_1 ,y_2$라고 하면 $$y^2-4my-4=0$$의 두근이다. 따라서 $$|y_1-y_2|^2=(y_1+y_2)^2-4y_1y_2=16(m^2+1)$$이다. 그러므로 $m=0$일 때, 즉 $\overline{AD}$가 대칭축에 수직일 때 최소가 된다. $x=1$와 포물선의 교점은 $(1,\pm 2)$이므로 최솟값은 $4$이다. 따라서 사다리꼴 $ABCD$의 둘레 길이의 최솟값은 $12$이다.
타원 위의 점 $(x_1, y_1)$에서 접선의 방정식은 $4x_1 x+9y_1 y=36$이다. 이 직선은 $x,y$축과 점 $\displaystyle{A(\bigg(\frac{9}{x_1},0\bigg),B(\bigg(0. \frac{4}{y_1}\bigg)}$에서 만난다. 따라서 삼각형 $OAB$의 넓이는
$$\triangle OAB =\frac{1}{2}\cdot \frac{9}{x_1}\cdot \frac{4}{y_1}=\frac{18}{x_1 y_1}$$
최솟값을 구하기 위해서는 $x_1 y_1$의 최댓값을 구해야 한다.
점 $(x_1, y_1)$은 타원 위의 점이므로 $4x_1^2+9y_1^2=36$을 만족한다. 따라서
$$\frac{4x_1^2+9y_1^2}{2}\geq \sqrt{4x_1^2\cdot 9y_1^2}=6x_1 y_1$$에서 최댓값 $3$임을 알 수 있다.
따라서 삼각형 넓이의 최솟값은 $6$이다.
6. 타원과 직선이 두점에서 만날 때, 그 교점들을 양 끝점으로 하는 선분들을 타원의 현이라 하자. 평행한 현들의 중점의 자취는 직선(선분)임을 보여라.
풀이보기타원 $\displaystyle{\frac{x^2}{a^2}+\frac{y^2}{a^2}=1}$이 직선 $y=mx+n$이 타원과 두 점 $$A(\alpha, m\alpha+n), B(\beta,m\beta+n)$$에서 만난다고 하자. 현 $\overline{AB}$ 중점을 $M(x,y)$이라고 하자.
$$x=\frac{\alpha+\beta}{2},y=\frac{m(\alpha+\beta)}{2}+n$$이다. 한편 두 방정식을 연립하면
$$b^2x^2+a^2(mx+n)^2=a^2b^2$$
$$(a^2 m^2 +b^2)x^2 +2a^2 mnx+a^2(n^2-b^2)=0$$
이다. 근과 계수와의 관계에 따라
$$x=\frac{\alpha+\beta}{2}=-\frac{a^2 mn}{a^2 m^2 +b^2}$$
$$y=\frac{m(\alpha+\beta)}{2}+n=-\frac{a^2m^2n}{a^2 m^2 +b^2}+n=\frac{nb^2}{a^2 m^2 +b^2}$$
이다. 그러므로 중점 $M$은 직선 $\displaystyle{y=-\frac{b^2}{a^2m}x}$위에 있다.
7. 장축의 길이가 $2a$, 단축의 길이가 $2b$이고 중심이 원점인 타원에서 $360^{\circ}$ 모든 방향으로 타원의 크기를 $c$만큼 일정하게 확장할 때, 이 때 만들어지는 그래프는 타원인지 아닌지 확인하여라.
풀이보기
아래 그림을 참고하여 확인하여라. 파란 색 타원은 붉은 색 타원을 장축과 단축 방향으로 $c$만큼 늘린 타원이고 붉은 점선으로 그려진 원은 $P$가 중심이고 반지름이 $c$인 원이다.
\overline{PF^{\prime}}=\overline{OP}^2$가 성립함을 보여라.(단 점 $F,F^{\prime}$는 쌍곡선의 초점이고 $O$는 원점이다.) 풀이보기
먼저 초점의 좌표를 $(\pm c ,0)$이라고 하면 $c^2 =a^2 +a^2=2a^2$이므로 두 초점은 $F^{\prime}(-a\sqrt2 ,0),F(a\sqrt2 ,0)$로 놓을 수 있다.
$$\overline{PF}\cdot \overline{PF^{\prime}}=\sqrt{(x_1-a\sqrt2)^2+y_1^2}\sqrt{(x_1+a\sqrt2)^2+y_1^2}$$
한편, 점 $P(x_1 ,y_1 )$ 쌍곡선 위의 점이므로 $x_1^2-y_1^2 =a^2$을 만족한다. 이를 이용하여 정리하면
$$=\sqrt{3x_1^2-y_1^2+2\sqrt2 ax_1}\sqrt{3x_1^2-y_1^2-2\sqrt2 ax_1}$$
$$=\sqrt{(3x_1^2-y_1^2)^2-8a^2x_1^2}=\sqrt{(3x_1^2-y_1^2)^2-8(x_1^2-y_1^2)x_1^2}$$
$$=\sqrt{x_1^4 +2x_1^2y_1^2 +y_1^4}=x_1^2 +y_1^2=\overline{OP}^2$$
1) 이차방정식 $16x^2 -24xy+9y^2 -60x+80y+100=0$의 그래프를 그려라.
풀이보기
$$\tan\theta=\frac{3}{4},-\frac{4}{3}$$이다.
$\displaystyle{\tan\theta=\frac{3}{4}}$라고 하면 $\displaystyle{\cos\theta=\frac{3}{5},\sin\theta=\frac{4}{5}}$이다.
$$\begin{pmatrix} x\\y \end{pmatrix}=\frac{1}{5}\begin{pmatrix}3 & -4\\ 4&3\end{pmatrix}\begin{pmatrix}x^{\prime}\\y^{\prime}\end{pmatrix}$$을 정리하여 대입하면
$$(y^{\prime})^2=4(x^{\prime}-1)$$을 얻을 수 있다. 이 포풀선의 초점은 $(2,0)$이고 준선은 $x^{\prime}=0$이다.
2) $xy$ 좌표계에서 초점을 구하여라.
정답 $$\bigg(\frac{6}{5},\frac{8}{5}\bigg)$$
3) $xy$ 좌표계에서 준선의 방정식을 구하여라.
정답 $$x=-\frac{4y^{\prime}}{5},y=\frac{3y^{\prime}}{5}$$이므로 준선은 $3x+4y=0$이다.
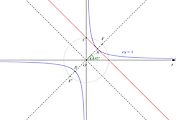
10. 쌍곡선의 두 점근선이 직교할 때, 이 쌍곡선을 직각쌍곡선이라 한다. 이차방정식 $Ax^2 +Bxy +Cy^2 +Dx+Ey+F=0$의 그래프가 쌍곡선으로 주어질 때, $A+C=0$이면 이 쌍곡선은 직각쌍곡선임을 보여라. (단 $A,B,C$는 모두 $0$이 아니다.)
풀이 대칭축이 좌표축이 되도록 $\displaystyle{\cot 2\theta=\frac{A-C}{B}}$를 만족하는 $\theta$ 회전이동한 쌍곡선의 방정식을 구해보자.
$$\begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix}\cos\theta & -\sin\theta\\ \sin\theta&\cos\theta\end{pmatrix}\begin{pmatrix}x^{\prime}\\y^{\prime}\end{pmatrix}$$
새롭게 얻어진 방정식을
$$A^{\prime}(x^{\prime})^2 +B^{\prime}x^{\prime}y^{\prime} +C^{\prime}(y^{\prime})^2 +D^{\prime}x^{\prime}+E^{\prime}y^{\prime}+F^{\prime}=0$$
라고 하면
$$$A^{\prime}=A\cos^2\theta+B\cos\theta\sin\theta+C\sin^2\theta$$
$$B^{\prime}=B\cos 2\theta-(A-C)\sin 2\theta$$
$$C^{\prime}=A\sin^2 \theta-B\cos\theta\sin\theta+C\cos^2\theta$$
이므로 $A^{\prime}+C^{\prime}=A+C, B^{\prime}=0$임을 보일 수 있다.
그러므로 $A+C=0$이면 $A^{\prime}=-C^{\prime}$이므로 주어진 쌍곡선은 직각쌍곡선이 된다.
11. 타원 $\displaystyle{\frac{x^2}{9}+{y^2}=1}$에 대하여
a) 점 $(x,y)$를 원점을 중심으로 $\displaystyle{\frac{\pi}{6}}$만큼 회전하여 점 $(X,Y)$를 얻었다. 다음 식을 만족하는 행렬 $A$를 구하여라.
$$\begin{pmatrix} X\\Y \end{pmatrix}=A\begin{pmatrix}x\\y\end{pmatrix}$$
정답
$$\begin{pmatrix} X\\Y \end{pmatrix}=\frac{1}{2}\begin{pmatrix}\sqrt3 & -1\\1&\sqrt3\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}$$
b) 주어진 타원을 원점을 중심으로 $\displaystyle{\frac{\pi}{6}}$만큼 회전한 식을 구하여라.
$$\begin{pmatrix} x\\y \end{pmatrix}=\frac{1}{2}\begin{pmatrix}\sqrt3 & 1\\-1&\sqrt3\end{pmatrix}\begin{pmatrix}X\\Y\end{pmatrix}$$
$$x=\frac{1}{2}(\sqrt3 X+Y) , y=\frac{1}{2}(-X+\sqrt3 Y)$$
를 주어진 식에 대입하여 정리하면
$$3X^2 -4\sqrt3 XY+7Y^2 =9 $$
c) (b)에서 회전된 타원에서 최고점의 좌표를 구하여라. 단 최고점은 타원 위의 점 중 $y$좌표값이 가장 큰 점이다.
풀이 (1)식을 $X$에 대하여 미분하면
$$3X-2\sqrt3 Y-4\sqrt3 XY^{\prime}+7YY^{\prime}=0$$
이다. 여기서 $Y^{\prime}$이 $0$이 될 때를 찾으면 된다. $3X-2\sqrt3Y=0$이다. $X=2\sqrt3 t, Y=3t$로 계산하면 $t=\pm \sqrt3 /3$을 얻을 수 있다. 그러므로 $(2,\sqrt3)$이 찾는 점이다.
12. 좌표평면에서 쌍곡선 $4x^2 -8y^2 =1$과 타원 $2x^2 +ay^2 =1$이 만나고 그 교점에서 두 곡선의 접선들이 서로 수직으로 만날 때, 상수 $a$의 값을 구하여라.
풀이 두 곡선의 교점을 $P(x_1,y_1)$이라고 하자. 점 $P$에서 접선의 방정식은 각각
$$4x_1x-8y_1y=1,\;2x_1x+ay_1y=1$$
이다. 이 접선이 서로 수직이므로 $$4x_1\times2x_1-8y_1\times ay_1=0$$이다. 정리하면
$$x_1^2-2ay_1^2=0----------(a)$$
한편 점 $P$가 두 곡선의 교점이므로
$$4x_1^2 -8y_1^2 =1,\;2x_1^2 +ay_1^2 =1$$
에서 $$2x_1^2-(8+a)y_1^2=0-----------(b)$$
(a),(b)에 의하여 $(a-8)y_1^2=0$이고 $y_1 \not=0$이므로 $a=8$이다.
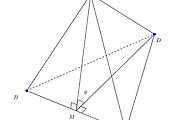
13. 포물선 $y^2 =4px$의 초점 $F$를 지나는 직선이 포물선과 만나는 점을 $P,Q$라 하고 점 $P,Q$에서 준선에 내린 수선의 발을 각각 $R,S$라고 할 때 다음을 보여라.
$$\overline{RS}^2 =4\overline{RP}\cdot \overline{SQ}$$
$$\overline{RM}=\overline{MF}=\overline{MS}$$
이므로 교점 $M$은 $\overline{RS}$의 중점이다.
$$(\overline{PF}+\overline{FQ})^2=\overline{PM}^2+\overline{QM}^2$$
포물선 정의에 따라
$$\overline{PF}=\overline{RP},\overline{QF}=\overline{SQ}$$
이다. 따라서
$$(\overline{RP}+\overline{SQ})^2=\overline{PM}^2+\overline{QM}^2$$
$$\overline{RP}^2+\overline{SQ}^2 +2\overline{RP}\cdot \overline{SQ}=\overline{PM}^2+\overline{QM}^2$$
이를 정리하면
$$2\overline{RP}\cdot \overline{SQ}=\overline{PM}^2-\overline{RP}^2+\overline{QM}^2-\overline{SQ}^2$$
$$2\overline{RP}\cdot \overline{SQ}=\overline{RM}^2+\overline{MS}^2$$
$\overline{RM}=\overline{MS}$이므로
$$\overline{RP}\cdot \overline{SQ}=\overline{RM}^2=\bigg(\frac{1}{2}\overline{RS}\bigg)^2$$
$$\therefore \overline{RS}^2 =4\overline{RP}\cdot \overline{SQ}$$
다른 풀이 점 $Q$에서 직선 $RP$에 내린 수선의 발을 $T$라고 하자.




 심수1_종합_202_2차곡선회전.pdf
심수1_종합_202_2차곡선회전.pdf