딸을 위한 피타고라스 정리 증명

중학교 2학년인 딸이 이제 막 피타고라스 정리(Pythagorean theorem)를 배우고 있다.

증명 1. 가장 유명한 증명인 '신부의 의자'다.

지오지브라로 보기

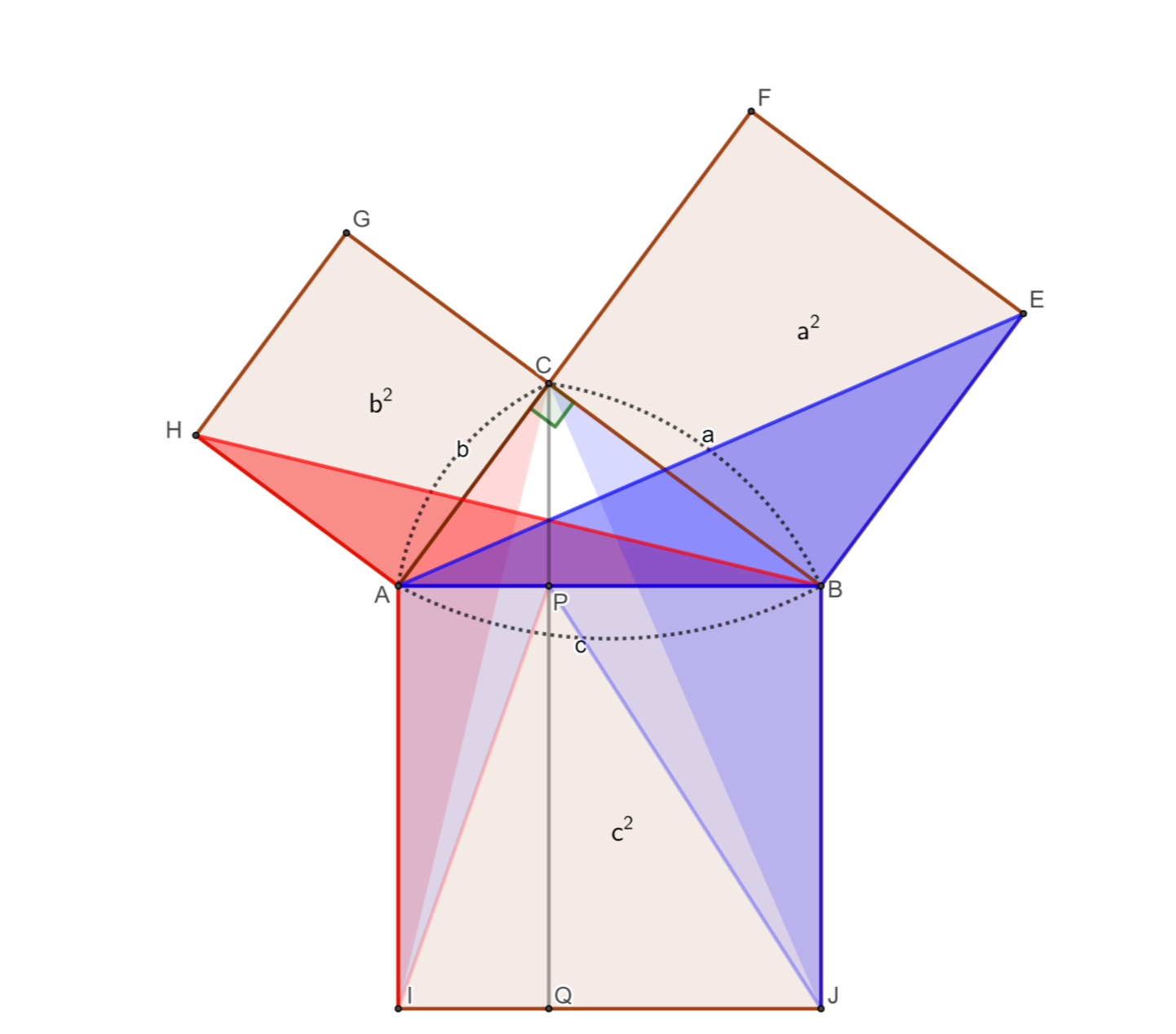
증명 2 아래 첫 번째 그림에서 직각 삼각형 둘을 회전하면 두 번째 그림이 된다. 넓이는 달라지지 않으므로 $a^2 +b^2 =c^2$이다.

지오지브라로 보기

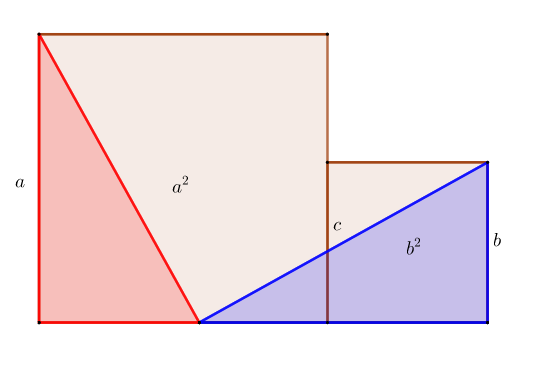
증명 3. 닮음으로 증명

$$\triangle ACD \sim \triangle CBD \sim ABC $$

$$c:a=a:DB\Rightarrow a^2 =c \times DB$$

$$c:b=b:AD \Rightarrow b^2 =c \times AD$$

$$a^2 +b^2 = c \times DB +c \times AD =c \times (DB + AD)=c^2$$

이것은 1번 증명에서도 쉽게 알 수 있다.

$$AE \times AD=b^2,\quad BF \times BD=a^2$$

증명 4. 직각 삼각형을 다시 배치함으로써 보일 수 있다.

증명 5. 곱셈 공식으로 보일 수도 있다.

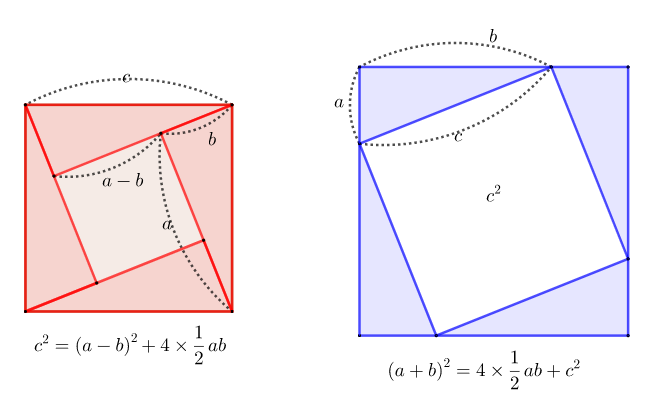
증명 6. 아래와 같이 사다리꼴을 삼각형으로 잘라서 보일 수도 있다.

증명 7. 사다리꼴을 조금 다르게 써서 보일 수도 있다.

$$2 b^2 = 2\times \frac{1}{2}\times (b+a) \times (b-a)+ \frac{1}{2}\times 2c \times c$$

증명 8.  넓이의 비는 닮음비의 제곱과 같다.

닮음비 $a:b:c$이므로 넓이는 각각 $ka^2 , kb^2, kc^2$으로 놓을 수 있다.

$$kc^2 =ka^2 +kb^2$$

지오지브라로 보기

 

---

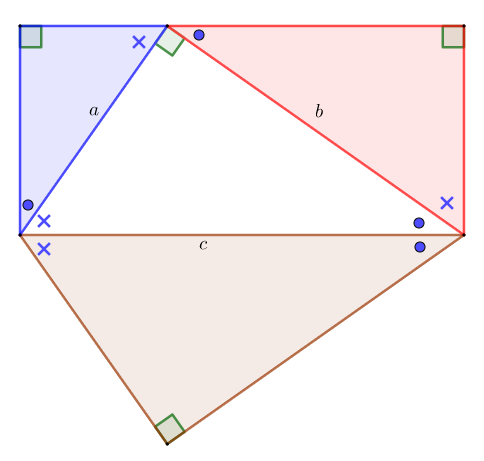
증명 9. 레오나르도 다빈치가 한 증명

아래 그림에 있는  두 육각형 $ABJIHG$와 $CADFEB$는 넓이가 같다. 한 변이 $a+b$인 정사각형에서 $\triangle ABC$와 같은 삼각형을 둘씩 잘라낸 다각형이기 때문이다.

넓이 $(ABJIHG)=$ 넓이$(CADFEB)$

$$a^2 +b^2 +\frac{1}{2}ab=c^2 +\frac{1}{2}ab$$

증명 10. 위 증명을 아래와 같이 바꿔서 보일 수도 있다.

증명 11. 구장산술에는 구고현의 정리로 부르는 정리와 증명이 있다. 변의 길이가 $3:4:5$일 때를 보이고 있다.

증명 12. 왼쪽은 아래와 같이 색종이 오려 붙이기로 보일 수 있다.

참고: 피타고라스 정리 증명 122

Pythagorean Theorem and its many proofs