끈 예술(string art)과 베지어 곡선(Bézier curves)

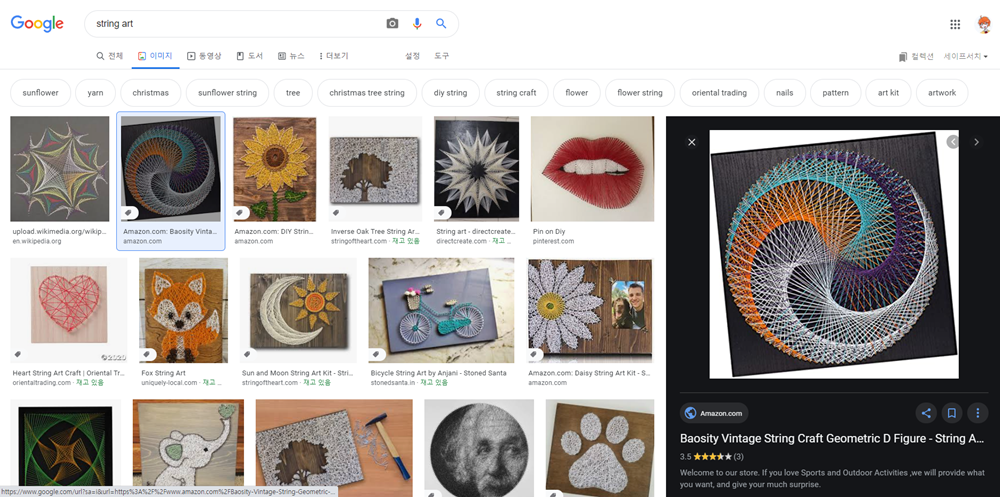
아래와 같이 끈을 매서 아름다운 곡선을 만들 수 있다. 이런 예술을 스트링 아트라고 부른다. 당연히 수학으로 해석할 수 있다. 이것은 포락선(envelope)과 베지어 곡선으로 이름 지어진 곡선과 관련이 있다.

Pixabay로부터 입수된 David Zydd님의 이미지 입니다.  

구글 검색 화면

포락선(envelope)

평면 곡선의 집합 $C_t$가 주어졌을 때, 집합 $C_t$의 원소인 모든 곡선과 어떤 점에서 접하는 곡선을 이 곡선 집합의 포락선이라고 한다. 

자세한 이야기는 아래 링크를 열어서 공부하기로 하자.

suhak.tistory.com/365

2017학년도 카이스트 일반전형 수학문제

스트링 아트에 쓰인 끈을 곡선 집합으로 생각하면 이들 직선으로 둘러싸인 곡선이 바로 포락선이다.

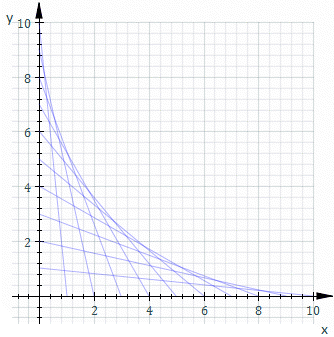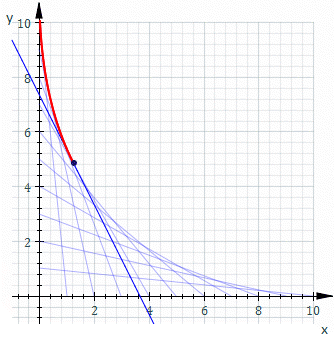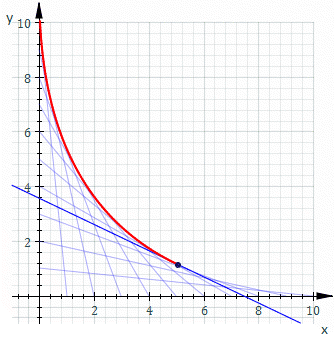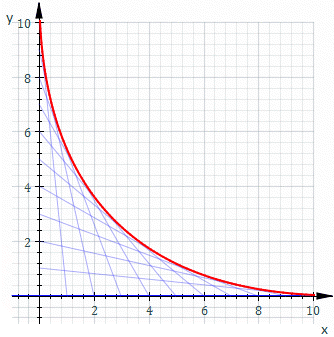
$P_1(10,0)$를 출발해서 원점 $(0,0)$까지 직선으로 움직이는 점 $M$과 원점 $(0,0)$에서 출발하여 점 $p_2(10,0)$까지 직선으로 움직이는 점 $N$이 있다고 하자. 두 점 $M,N$이 모두 일정한 속력으로 움직일 때 두 점을 잇는 직선 $MN$의 집합이 생긴다. 선분 $MN$위를 일정한 속력으로 움직이는 점이 그리는 자취가 바로 포락선이 된다. 

베지어 곡선에 대해 알아 보자. 포락선인 붉은 곡선은 베지어 곡선이기도 하다.

베지어 곡선

베지어 곡선은 컴퓨터 그래픽에 쓰이는 매개변수 곡선이다. 번스타인 다항식(Bernstein polynomial)과 연관된 곡선이지만 1960년 르노 자동차 디자이너인 피에르 베지어(Pierre Bézier)에서 이름을 따왔다. 요즘 컴퓨터에서 쓰는 글꼴을 디자인하거나 애니메이션을 만들 때도 쓰인다. 일러스트레이터를 비롯한 다양한 프로그램에 베지어 곡선이 들어 있다.

먼저 간단한 경우를 살펴 보자.

1차 베지어 곡선

서로 다른 두 점 $P_0$와 $P_1$이 주어졌다고 하자. $P_0$에서 출발하여 $P_1$까지 일정한 속력으로 움직이는 점이 그리는 자취를 찾아보자. 아래와 같이 시각 $t$에 대한 방정식으로 결정된다. 이 곡선을 1차 베지어 곡선이라고 하는데 결국 두 점을 잇는 선분이다.   

$$\mathbf{B}(t)=\mathbf{P}_0 + t(\mathbf{P}_1-\mathbf{P}_0)=(1-t)\mathbf{P}_0 + t\mathbf{P}_1 \mbox{ , } 0 \le t \le 1$$

마지막 식을 보면 결국 베지어 곡선 위의 점은 선분 $P_0P_1$을 $t:1-t$로 내분하는 점을 찾는 선형 보간법으로 결정된다.

$t$에 대하여 미분하면 상수이므로 등속 운동함을 알 수 있다.

$$\mathbf{B}^{\prime}(t)=\mathbf{P}_1 -\mathbf{P}_0  \mbox{ , } 0 \le t \le 1$$

이제는 고등학교 과정에서 사라진 기하와 벡터에 있는 직선의 방정식을 생각하면 쉽게 이해할 수 있다. 점 $P_0$를 지나고 방향 벡터가 $\overrightarrow{\mathbf{P}_0 \mathbf{P}_1}$인 직선의 방정식은 아래와 같다.

$$\mathbf{B}(t)=\mathbf{P}(t)=\mathbf{P}_0 + t\overrightarrow{\mathbf{P}_0 \mathbf{P}_1}$$

2차 베지어 곡선

2차 베지어 곡선을 그리기 위해서는 세 점이 필요하다. 주어진 점 $P_0$, $P_1$, $P_2$이 있을 때 위에서와 같이 점 $M$은 $P_0$에서 $P_1$까지 직선을 따라 일정한 속력으로 움직이고 점 $N$은 $P_1$에서 $P_2$까지 직선을 따라 일정한 속력으로 움직인다고 하자. 선분 $MN$위를 일정한 속력으로 움직이는 점의 자취가 바로 2차 베지어 곡선이다.

다시 말하면 $M$과 $N$은 1차 베지어 곡선 위에 있는 점이고 $M$과 $N$으로 결정되는 1차 베지어 곡선 위의 점이 그리는 자취가 바로 2차 베지어 곡선이다. 시간 $t$에 따라 결정되는 함숫값 $B(t)$에 의하여 정해지는 곡선이다.

$$\mathbf{B}(t) = (1 - t)[(1 - t) \mathbf P_0 + t \mathbf P_1] + t [(1 - t) \mathbf P_1 + t \mathbf P_2] \mbox{ , } 0 \le t \le 1$$

2차 베지어 곡선은 각각 $P_0$에서 $P_1$까지, $P_1$에서 $P_2$까지의 1차 베지어 곡선 위에 있는 점을 선형 보간법에 따라 정해지는 곡선이다. 위 식을 다시 정리하면 아래와 같다.

$$\mathbf{B}(t) = (1 - t)^{2}\mathbf{P}_0 + 2(1 - t)t\mathbf{P}_1 + t^{2}\mathbf{P}_2 \mbox{ , } 0 \le t \le 1.$$

2차 베지어 곡선

bezier.ggb

0.01MB

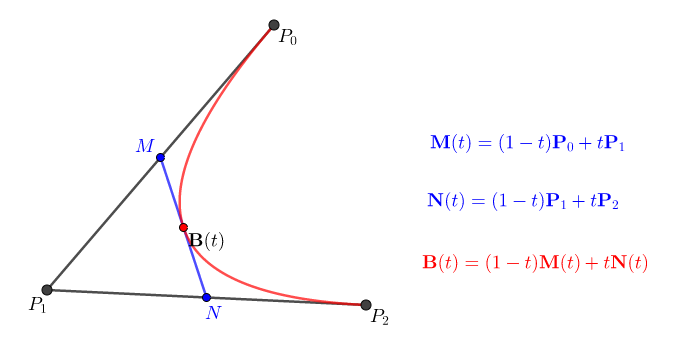
$P_1$에 대하여 대칭적으로 정리하면 아래와 같다.

$$\mathbf{B}(t) = \mathbf{P}_1+(1 - t)^{2}(\mathbf{P}_0 - \mathbf{P}_1) + t^{2}(\mathbf{P}_2-\mathbf{P}_1) \mbox{ , } 0 \le t \le 1.$$

이 식을 $t$에 대하여 미분하면 다음과 같다.

$$\mathbf{B}'(t) = 2 (1 - t) (\mathbf{P}_1 - \mathbf{P}_0) + 2 t (\mathbf{P}_2 - \mathbf{P}_1) .$$

$0<t<1$일 때를 생각해 보면 $P_0$를 출발하여 $P_1$쪽으로 휘어지면서 방향을 바꾸다가 $P_2$에 도착한다.

$t$에 대하여 한 번 미분한 이계도함수를 구하면 아래와 같다. 등가속도 운동을 한다.

$$\mathbf{B}''(t) = 2(\mathbf{P}_2 - 2 \mathbf{P}_1 + \mathbf{P}_0) .$$

여기서 2차 베지어 곡선은 포물선이 될 것임을 알 수 있다.

 

3차 베지어 곡선

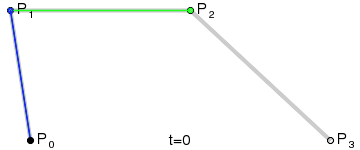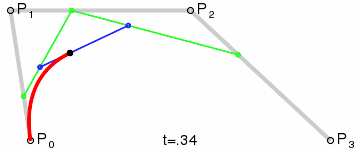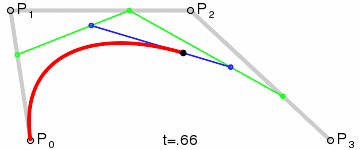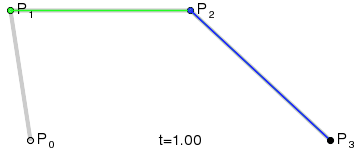
3차 베지어 곡선은 같은 평면에 있는 서로 다른 네 점 $P_0$, $P_1$, $P_2$, $P_3$에 따라 결정된다. 세 점으로 결정되는 2차 베지어 곡선을 각각 $\mathbf{B}_{\mathbf P_0,\mathbf P_1,\mathbf P_2}(t)$와 $\mathbf{B}_{\mathbf P_1,\mathbf P_2,\mathbf P_3}(t)$이라고 하면 3차 베지어 곡선은 아래와 같이 정해진다.

$$\mathbf{B}(t)=(1-t)\mathbf{B}_{\mathbf P_0,\mathbf P_1,\mathbf P_2}(t) + t \mathbf{B}_{\mathbf P_1,\mathbf P_2,\mathbf P_3}(t) \mbox{ , } 0 \le t \le 1.$$

양함수 꼴로 다시 정리하면 아래와 같다.

$$\mathbf{B}(t)=(1-t)^3\mathbf{P}_0+3(1-t)^2t\mathbf{P}_1+3(1-t)t^2\mathbf{P}_2+t^3\mathbf{P}_3 \mbox{ , } 0 \le t \le 1.$$

이 곡선은 $P_0$에서 출발하여 $P_1$을 향하다가 휘어지면서 $P_2$를 향하다가 $P_3$에서 끝나는 곡선이다.

 

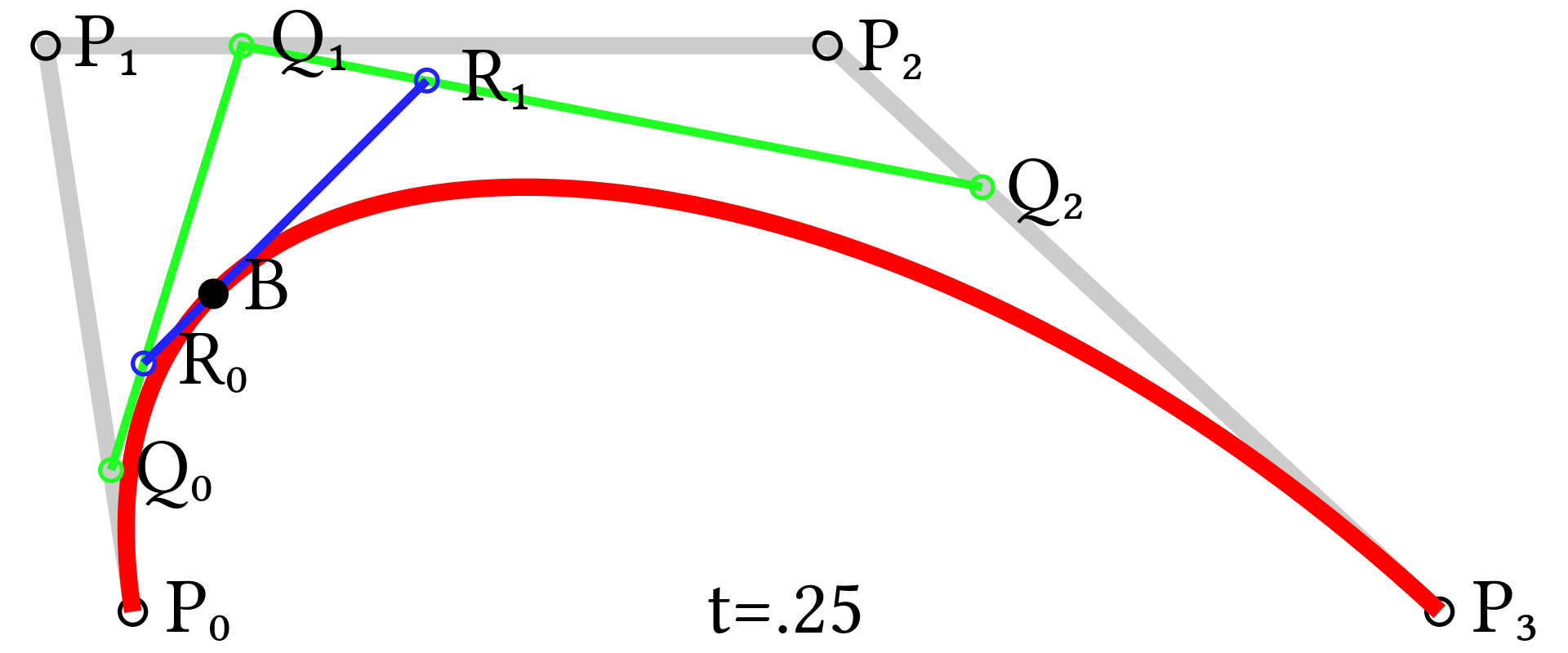
이제 같은 방식으로 점을 추가하면서 곡선을 그리면 된다. 4차 베지어 곡선은 아래와 같다.

 

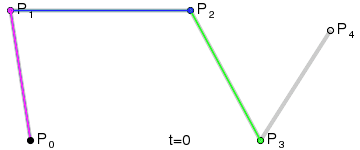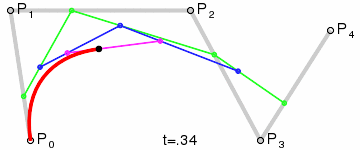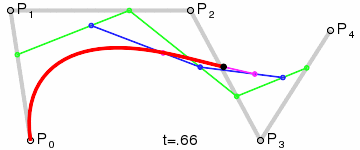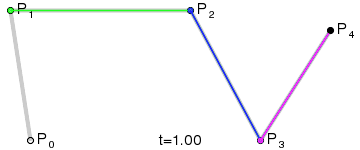
점화식으로 정의

$n$차 베지어 곡선은 점화식으로 정의할 수 있다.

$\mathbf{B}_{\mathbf{P}_0\mathbf{P}_1\ldots\mathbf{P}_n}$은 $P_0, P_1,\cdots ,P_n$으로 만들어지는 $n$차 베지어 곡선이라고 하자.

$$\begin{split}&\mathbf{B}_{\mathbf{P}_0}(t) = \mathbf{P}_0 \\ & \mathbf{B}(t) = \mathbf{B}_{\mathbf{P}_0\mathbf{P}_1\ldots\mathbf{P}_n}(t) = (1-t)\mathbf{B}_{\mathbf{P}_0\mathbf{P}_1\ldots\mathbf{P}_{n-1}}(t) + t\mathbf{B}_{\mathbf{P}_1\mathbf{P}_2\ldots\mathbf{P}_n}(t)\end{split}$$

밖으로 드러낸 정의

위에 있는 점화식을 정리하여 일반적인 공식을 정리하면 아래와 같다.

$$\begin{align}\mathbf{B}(t) &= \sum_{i=0}^n {n\choose i}(1 - t)^{n - i}t^i\mathbf{P}_i \\&=(1 - t)^n\mathbf{P}_0 + {n\choose 1}(1 - t)^{n - 1}t\mathbf{P}_1 + \cdots + {n\choose n - 1}(1 - t)t^{n - 1}\mathbf{P}_{n - 1} + t^n\mathbf{P}_n && 0 \leqslant t \leqslant 1\end{align}$$

위 식에서 $\displaystyle{{n \choose i}}$는 이항계수이다.

예를 들면 5차 베지어 곡선은 아래와 같다.

$$\begin{align}\mathbf{B}(t) &= (1 - t)^5\mathbf{P}_0 + 5t(1 - t)^4\mathbf{P}_1 + 10t^2(1 - t)^3 \mathbf{P}_2 + 10t^3 (1-t)^2 \mathbf{P}_3 + 5t^4(1-t) \mathbf{P}_4 + t^5 \mathbf{P}_5 && 0 \leqslant t \leqslant 1 \end{align}$$

 

더 깊이 공부하고 싶다면 아래 링크를 열어 보자.

en.wikipedia.org/wiki/B%C3%A9zier_curve

Bézier curve - Wikipedia