2021학년도 수능 수학 가형 20번

올해 2021학년도 수능은 다른 해와 달리 20번이 매우 어렵다. 이 문제에 시간을 많이 쓰게 된 학생이 매우 많을 듯하다.

20. 함수 $f(x)=\pi \sin 2\pi x$에 대하여 정의역이 실수 전체의 집합이고 치역이 집합 $\{0,1\}$인 함수 $g(x)$와 자연수 $n$이 다음 조건을 만족시킬 때, $n$의 값은? [4점]

---

함수 $h(x)=f(nx)g(x)$는 실수 전체의 집합에서 연속이고
$$\int_{-1}^{1}h(x)dx=2,\quad\quad \int_{-1}^1 x h(x)dx=- \frac{1}{32}$$이다.

---

풀이

먼저 함수 $f$는 실수 전체의 집합에서 연속이다. 연속인 함수에 0 또는 1을 곱한 함수가 연속이 될 조건을 생각해 보자. 두 함수가 모두 연속인 점은 저절로 곱한 함수도 연속이 되므로 생각하지 않아도 된다. 함수 $g$가 $x=a_k$에서 불연속이라고 하자. $f(na_k)g(x)$의 좌우 극한이 모두 0이 되어야 함수 $h$가 연속이다. 따라서 함수 $g$가 불연속인 점은$a_k=k/2n$($k$는 정수)의 꼴이다.

함수 $f(nx)=\pi \sin 2n\pi x$의 함숫값을 신호로 생각하면 함숫값 $g(x)$가 0인 구간은 신호를 없애고 1인 구간은 신호를 그대로 둔다고 볼 수 있다. 

그래프를 그려 보자. 함수 $f(nx)=\pi \sin 2n \pi x$는 주기가 $1/n$이다. 함숫값이 양수인 구간과 음수인 구간을 적당히 그대로 두거나 0으로 만든 새로운 함수 $h$를 만든다. 조건에 주어진 정적분 구간이 0을 기준으로 대칭이므로 함수 그래프가 가진 대칭성에 주목하자.

먼저 $$\int_{0}^{1/2n}h(x)dx=\int_{0}^{1/2n}\pi\sin 2n\pi xdx=\frac{1}{n}.$$

따라서 $$\int_{-1}^{1}h(x)dx=2$$이기 위해서는 함숫값 $f(nx)$가 양수인 부분은 모두 남아 있고 음수인 부분은 0이 되어야 한다.

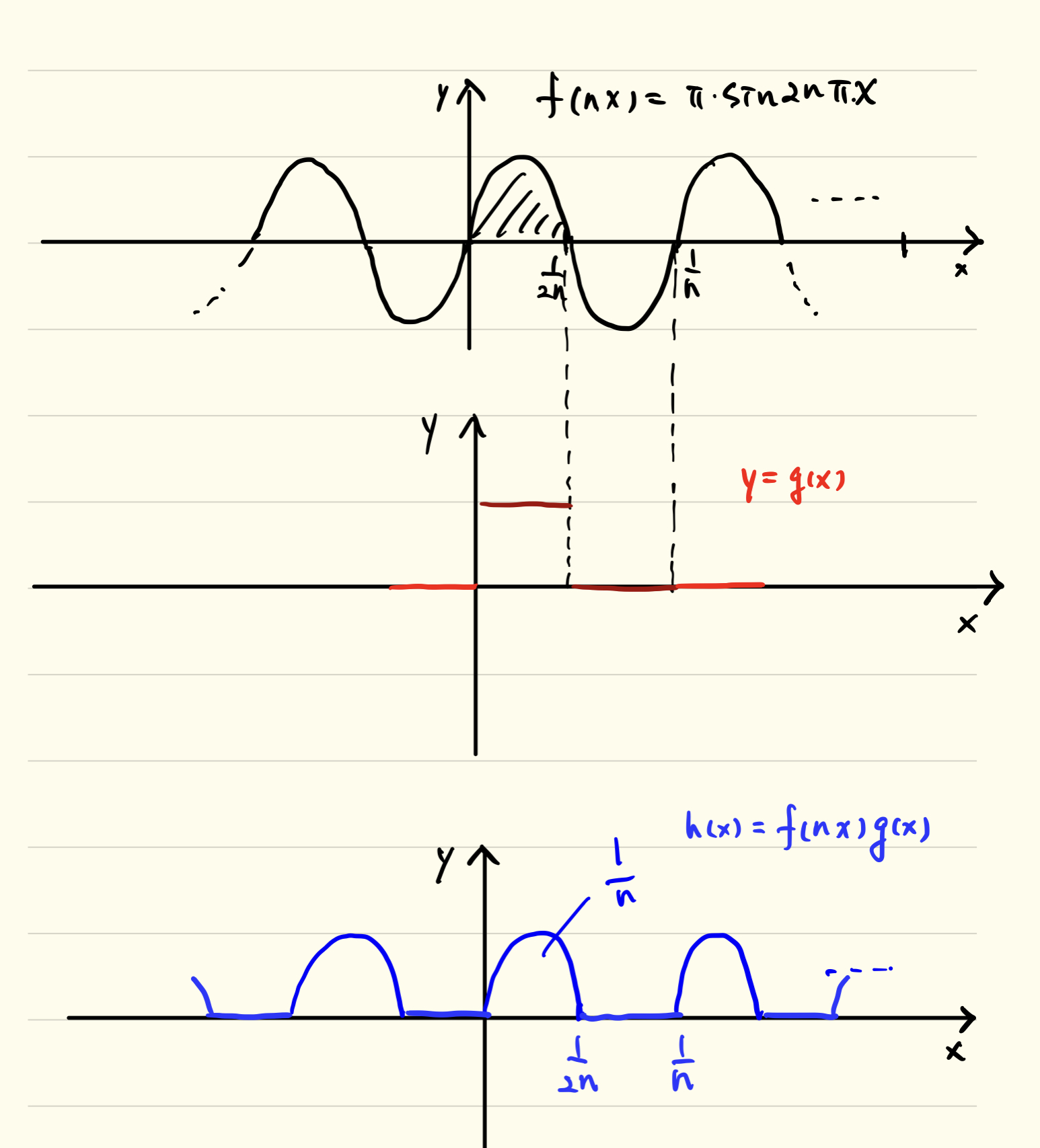
파란 색으로 그린 그래프는 일단 개형을 그렸다고 보면 된다.

이제 조건에 있는 두 번째 정적분을 살펴보자. 먼저 함숫값 $xh(x)$을 생각해 보자. $x \geq 0$일 때, $xh(x)\geq 0$이고 $x<0$일 때 $xh(x) \leq 0$이다.

아래 그림과 같이 제3 사분면에 있는 그래프를 제4 사분면으로 $y$축에 대칭인 위치로 이동한 다음 적분해도 결과는 같다.

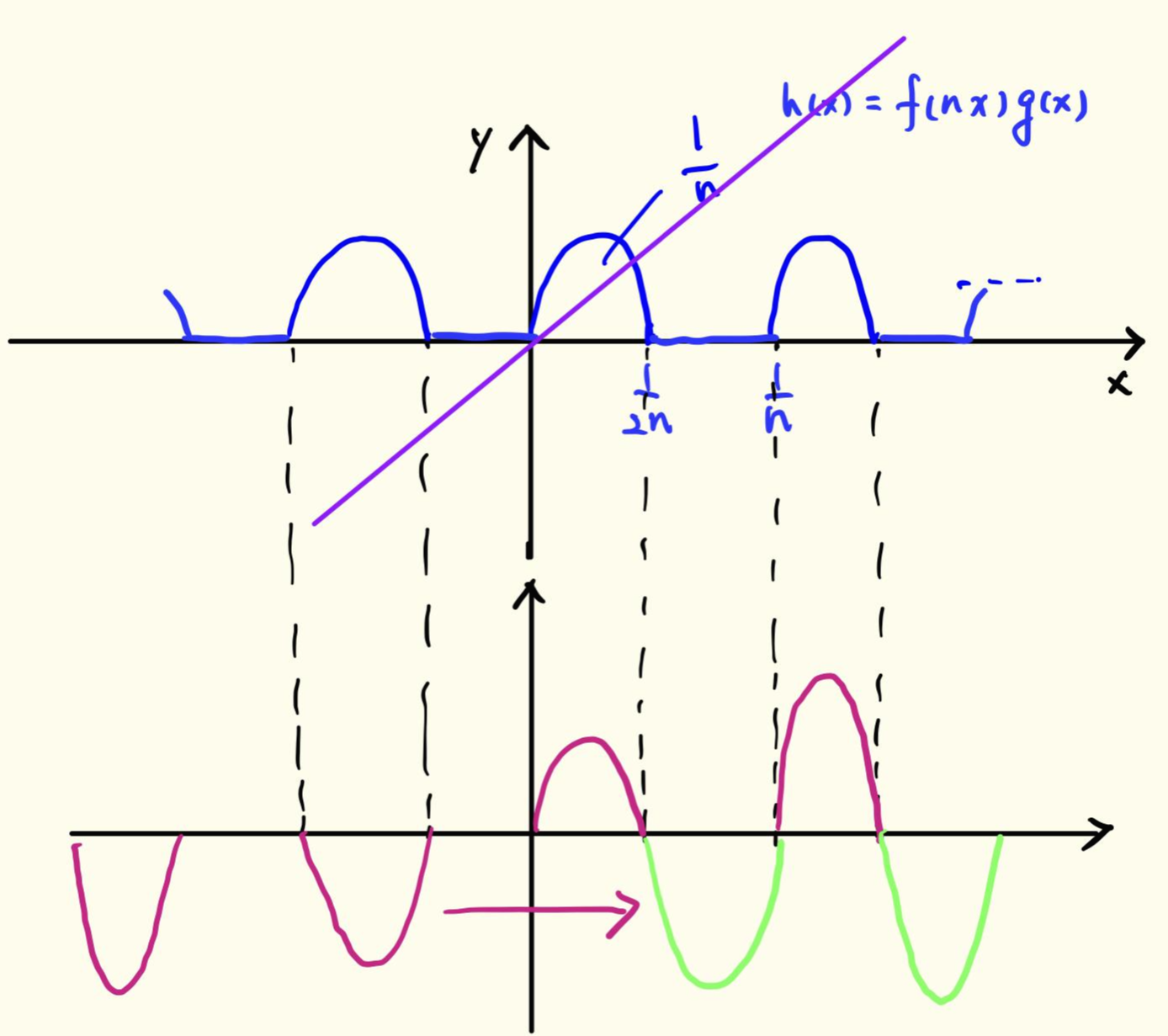
$$ \int_{-1}^1 x h(x)dx=\int_{0}^{1}x \pi\sin 2n\pi x dx.$$

부분 적분으로 계산하면

$$ \bigg[-x \frac{1}{2n} \cos 2 n \pi x \bigg]_0^1 +\frac{1}{2n} \int_{0}^{1} \cos 2n\pi x dx=-\frac{1}{2n}+\bigg[\frac{1}{4n^2 \pi} \sin 2n\pi x \bigg]_{0}^{1}=-\frac{1}{2n}.$$

마무리 계산을 하면

$$\frac{1}{2n}=\frac{1}{32}.$$ 

$$n=16.$$

처음에 풀었던 풀이는 너무 복잡해서 20번 문제가 이럴 수 없다는 생각으로 더 간단한 풀이를 겨우 찾았다. 이렇게 시험 시간에 풀었다면 실력을 인정한다. 수능 시험 문제 출제하는 사람도 존경스럽다. 도대체 이런 문제를 어떻게 생각해 내는 걸까 궁금하다. 다 풀고 나서 생각하니 요즘 공부하고 있는 기계 학습이나 딥 러닝에서 쓰는 시그넘 함수나 계단 함수와 연관되었다고 생각할 수 있겠다.