중학생이 알아야 하는 기본 도형

중학교 1학년 기본 도형은 '기하'를 공부하는 데 바탕이 되는 단원이다. 이제는 선택과목이 된 '기하와 벡터'는 많은 학생을 울리던 과목이다. 중학교와 고등학교에서 우리가 배우는 기하는 모두 유클리드 기하이다. 당연히 유클리드 '원론'으로 공부를 시작하면 좋다. 하지만 원론처럼 짜임새 있게 공부하려면 시간도 많이 필요하고 너무 어려우므로 오늘날 교과서는 쉽고 편하게 가르치기 위해 조금 다른 표현을 쓰고 있다. 원론처럼 공부하고 싶다면 이 블로그 글갈래를 참고하시라. 여기서는 그냥 맛보기로 정의만 소개하고 위치 관계를 살펴보려고 한다.

1. 점은 부분이 없는 것이다.
2. 선은 폭이 없는 길이이다.
3. 선의 끝은 점이다.
4. 직선이란 그 위의 점이 한쪽 옆으로 간 선이다.
5. 면은 길이와 폭만 있는 것이다.
6. 면의 끝은 선이다.
7. 평면이란 그 위의 직선이 한쪽 옆으로 간 면이다.

8. 평면각이란 평면 위에 있으면서 서로 만나되 하나의 직선이 안 되도록 위치한 두 선 사이의 기울기이다.
9. 각을 만드는 선이 둘 다 직선일 때, 그 각을 '직선각'이라고 한다.
10. 한 직선이 다른 한 직선과 만나고 있을 때, 이웃한 각이 서로 같으면 그 각을 직각이라고 한다.

11. 둔각(뭉툭한 각, 무딘 각)은 직각보다 큰 각이다.

12. 예각(뾰족한 각)은 직각보다 작은 각이다.

13. 둘레(경계)는 어떤 것의 끝이다.

14. 도형(꼴)은 둘레나 둘레들에 둘러싸인 것이다.

15. 원이란 평면 위의 한 점에서 그 위에 있으면서 선분의 길이가 언제나 같게 되는 하나의 선에 의하여 둘러 쌓인 평면 도형이다.
16. 그 한 점을 원의 중심이라고 한다.

17. 원의 지름은 중심을 지나고 양쪽 모두 원둘레에서 만나는 직선이다. 지름은 원을 이등분한다.

18. 지름과 지름이 자른 원둘레가 둘러싼 도형을 반원이라고 부른다. 반원의 중심은 원 중심과 같다.

19. 다각형은 직선들로 둘러싼 도형이다. 삼각형은 직선 셋으로 사각형은 직선 넷으로 둘러싼 도형이다.

20. 삼변형 가운데 세 변이 같은 것을 등변 삼각형, 두 변만이 같은 것을 이등변 삼각형, 세 변이 모두 같지 않은 것을 부등변 삼각형이라고 한다.

21. 직각삼각형은 직각을 가진 삼각형이다. 둔각 삼각형은 둔각을 가진 삼각형이다. 예각 삼각형은 세 각이 모두 예각인 삼각형이다.

22. 정사각형은 변이 모두 같고 각이 모두 직각인 사각형이다. 직사각형은 각이 모두 직각인 사각형이다. 마름모는 변이 모두 같은 사각형이다. 평행사변형은 마주 보는 변들이 서로 평행한 사각형이다. 이들 이외의 사각형들을 부등변 사각형이라 부른다.

23. 평행선이란 같은 평면 위에 있으면서 양쪽을 아무리 연장하여도 어느 방향에서도 만나지 않는 직선이다.

 

기본 도형

점, 선, 면

아무것도 없는 곳에도 점은 있다. 점은 부분이 없는 것이다. 아무것도 없는 점이지만 움직이면 선이 생긴다. 선은 폭은 없고 다만 움직인 거리 즉, 길이만 있다. 선은 폭이 없는데 폭이 생기도록 움직이면 면이 된다. 면은 폭과 길이만 있고 두께는 없다. 현대 수학책은 점, 선, 면은 굳이 따로 정의(약속)하지 않고 그냥 쓴다. 중학교 교과서에서는 기본 요소라고 쓰고 있다. 직선과 평면도 마찬가지로 따로 약속하지는 않는다. 직선은 점이 일정한 방향으로만 움직인 선이고 직선을 일정한 방향으로 움직여 폭을 만든 면이 평면이라고 생각하면 된다.

귀찮고 어려워도 점, 선, 면처럼 약속하지 않고 용어를 마구 쓸 수 없다. 따라서 교과서에 갑자기 많은 용어가 튀어나온다. 앞으로 쉽게 통하기 위해서 교과서에 나오는 약속을 모두 정확하게 기억해 두어야 한다.

직선, 반직선, 선분

한 점을 지나는 직선은 무수히 많으나 서로 다른 두 점을 지나는 직선은 오직 하나뿐이다. 두 점 $A$, $B$를 지나는 직선 $AB$를 기호로 $\overleftrightarrow{AB}$ 또는 $\overleftrightarrow{BA}$로 적는다. 간단하게 소문자로 $l$로 나타내기도 한다.

직선 $AB$ 위에서 점 $A$에서 시작해서 점 $B$ 쪽으로 한없이 뻗은 반직선 $AB$를 기호로 $\overrightarrow{AB}$와 같이 적는다. 시작점을 앞에 써야 하므로 당연히 $\overrightarrow{BA}$로 쓴 것은 다른 반직선이다.

직선 $AB$ 위의 점 $A$에서 점 $B$까지의 부분인 선분 $AB$를 기호로 $\overline{AB}$ 또는 $\overline{BA}$로 적는다. 선분 $AB$의 길이를 두 점 A, B 사이의 거리라고 한다. $\overline{AB}$는 선분을 나타내기도 하고 길이를 나타내기도 한다. 선분 $AB$와 선분 $CD$의 길이가 같다면 $$\overline{AB}=\overline{CD}$$로 적는다.

선분 $AB$  위의 점 $M$에 대하여

$$\overline{AM}=\overline{MB}$$일 때, 점 $M$은 선분 $AB$의 중점이라고 한다.

각

두 반직선 $OA$와 $OB$로 이루어진 도형을 각 $AOB$라 하고 기호로

$$\angle AOB$$

로 적는다. 간단히 $\angle O$ 또는 $\angle a$로 나타내기도 한다. 각의 꼭짓점, 각의 변, 각의 크기를 확인하자. 

그림에서 두 반직선이 이루는 각은 안쪽과 바깥쪽이 있는데, 특별한 말이 없다면 $\angle AOB$는 보통 그림과 같이 크기가 작은 쪽을 읽는다.

평각과 직각이라는 특별한 각이 있다. 세 점 $A, O, B$가 한직선 위에 있다면 $\angle AOB$를 평각이라고 부른다. 크기는 $180^{\circ}$이다. 평각을 반으로 나눈 크기가 $90^{\circ}$인 각을 직각이라고 부른다.

크기가 $0^{\circ}$와  $90^{\circ}$ 사이인 뾰족한 각은 예각, 크기가  $90^{\circ}$와  $180^{\circ}$ 사이인 뭉툭한 각은 둔각이라고 한다.

맞꼭지각

두 직선이 한 점에서 만날 때는 만들어지는 네 각 $\angle a, \;\; \angle b, \;\;\angle c, \;\;\angle d$를 두 직선의 교각이라고 한다. 이때 서로 마주 보는 각을 맞꼭지각이라고 한다.

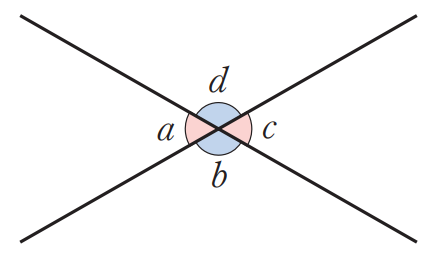
맞꼭지각은 서로 같다.

그림을 보면 그냥 알 수 있는 사실이지만 왜냐고 물으면 잠깐 주춤하는 학생이 많다. 맞꼭지각이 서로 같다는 걸 외우고 있다면 80점이고 그 이유를 말할 수 있다면 100점이다.

$$\angle a +\angle d=180^{\circ}=\angle d + \angle c$$

양변이 모두 평각이다. 같은 것에서 같은 것을 빼도 서로 같다.

$$\angle a +\angle d -\angle d =\angle d + \angle c -\angle d$$

$$\therefore \quad \angle a = \angle c$$

마찬가지로

$$\angle b = \angle d$$

이다. 기원전을 살았던 수학자 탈레스도 알았으니 요즘을 사는 우리는 당연히 알아야 한다.

두 직선 $AB$와 $CD$가 만날 때 생기는 교각이 모두 같다면 직각이다. 직각으로 만나는 두 직선을 직교한다고 한다. 이것을 기호로

$$\overleftrightarrow{AB} \;\; \bot \;\; \overleftrightarrow{CD}$$

로 적는다. 서로를 다른 직선의 수선이라고 한다. 요즘은 한자를 배우지 않아서 수학에서 쓰는 한자말로 된 용어가 쉽게 이해되지 않을 수 있다. 자꾸 읽고 외워야 한다. 때로는 수학 용어를 영어로 찾아보는 것도 도움이 된다. 예각은 'acute angle', 둔각은 'abtuse angle'이다. 북한에서는 '뾰족각'과 '무딘각'으로 부른다고 한다. '직각'은 'right angle'이다. 우리말로 옮기면 '올바른 각'이다. 기둥을 똑바로 세울 때 만들어지는 각이니 직각은 '올바른 각'이라고 생각하면 어떨까!