삼각형의 합동

삼각형의 합동은 삼각형이 단 하나로 결정되기 위해 필요한 조건과 밀접한 관계가 있다. 

삼각형의 결정 조건
1. 세 변의 길이가 주어졌다. 원론 명제 22
2. 두 변의 길이와 사이에 끼인 각의 크기가 정해졌다.
3. 한 변의 길이와 양 끝 각의 크기가 주어졌다.

세 변의 길이도 아무렇게나 주어지면 안 되고 두 변의 길이의 합이 나머지 한 변의 길이보다 커야만 한다.(원론 명제 20) 삼각형의 내각의 합은 180도이므로 양 끝 각이 아니더라고 두 각의 크기가 주어지면 되지만 보통 양 끝 각이라고 말한다.

유클리드 원론의 공통 관념(common notion) 4에 따라 포개어서 빈틈없으면 서로 같다. 두 삼각형 $\triangle ABC$와 $\triangle DEF$가 모양과 크기가 같아서 서로 완전히 겹쳐진다면 두 삼각형은 서로 합동이라고 한다. 기호로는

$$\triangle ABC\equiv\triangle DEF$$

로 적는다. 이때 두 삼각형의 꼭짓점은 대응하는 차례대로 쓴다.

합동을 말하기 전에 먼저 선분과 각을 옮기는 작도를 알아야 한다.

1. 선분 옮기기

선분은 컴퍼스로 길이를 재서 옮기면 된다. 당연해 보이지만 이것도 길이를 재서 옮길 수 있음을 보여야 한다. 원론 1권 명제 2를 증명하면 된다.

2. 각을 옮기기 1권 명제 23

$\angle AOB$를 옮겨서 점 $O_1$을 꼭짓점으로 하는 각을 작도하자. 

1) 각의 변 위에 적당한 점 $C$를 잡는다. 

2) $\overline{OC}$를 반지름으로 원을 그리고 반직선 $OA$와의 교점 $D$를 찾는다.

3.) 점 $O_1$을 중심으로 반지름이 $\overline{OC}$인 원을 그려서 점 $E$를 찾는다.

4) 점 $E$를 중심으로 반지름이 $\overline{CD}$인 원을 그려서 점 $F$를 찾는다.

 

 

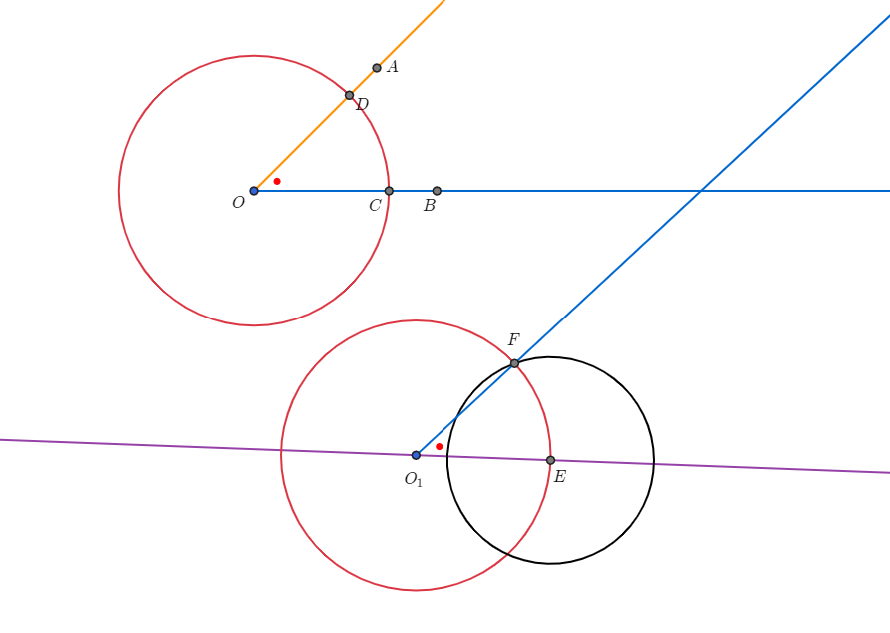
$$\angle{AOB}=\angle{FO_1 E}$$

선분과 각을 옮기는 과정은 합동과 자연스럽게 연결된다. 

중학교에서는 삼각형의 합동 조건은 증명 없이 그냥 참이라고 외우면 된다. 간단하게 영어로 적을 때 변은 Side, 각은 Angle의 머릿글자를 따서 적는다.

삼각형의 합동

1. 세 변의 길이가 서로 같다.(SSS합동): 원론 1권 명제 8 

2. 두 변의 길이와 사이에 끼인 각의 크기가 서로 같다.(SAS합동) 원론 1권 명제4

 

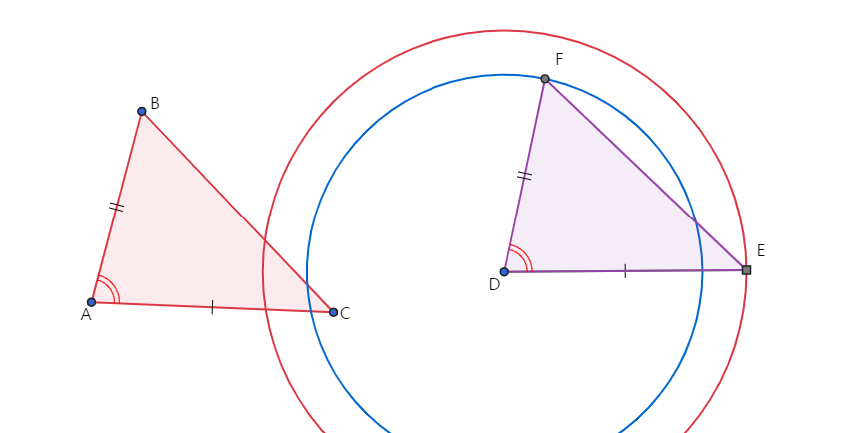
3. 한 변의 길이와 양 끝 각의 크기가 서로 같다.(ASA합동)

 

직각삼각형에서 직각을 끼고 있는 두 변이 같다면 SAS합동이다. 직각삼각형은 피타고라스 정리에 따라 두 변의 길이를 알면 나머지 한 변의 길이를 알 수 있다. 따라서 직각삼각형은 빗변과 다른 한 변이 같다면 SSS합동, 빗변과 다른 한 각이 서로 같으면 ASA 합동이다. 이를 간단하게 RHS합동, RHA합동으로 부른다. 참고로 직각은  Right angle이고 빗변은 영어로 Hypotenuse이다.