분수의 역사

어린 시절 수를 처음 배울 때, 수는 당연히 자연수만 존재한다. 하나, 둘, 셋 $\cdots$ 하지만 조금만 더 지나면 하나보다 작은 것이 있음을 깨닫는다. 그러나 하나가 부서진 조각을 수로 인식하는 것은 쉽지 않다. 자연수가 부서진 조각인 분수를 수로 나타내고 계산하는 것은 상당히 어려운 일이어서 많은 초등학생이 분수 때문에 수학을 포기하기도 한다.

역사를 공부하면 도움이 되지 않을까 싶어 정리해 둔다. 기원전 1000년 경 이집트 린드 파피루스에 분수가 나온다고 하니 어찌보면 그 역사가 제법 길다.

이집트 분수

 

표기법

분수를 어떻게 나타냈을까?

입을 나타내는 문자 아래에 숫자를 나타내는 문자를 써서 분수를 나타냈다. (참고 이집트 숫자 표기)

이집트인은 분자가 1인 단위분수를 주로 사용하였다. 아래와 같은 특별한 모양의 분수를 함께 사용하였다.

아래와 같은 단위분수의 합을 이집트 분수라고 한다.

$$\frac{1}{2}+\frac{1}{6}+\frac{1}{16}$$

위를 계산하면 $43/48$이다. 모든 양의 유리수는 $2/3$, $3/4$를 포함한 단위분수의 합으로 나타낼 수 있다. 이런 분수는 고대 이집트인들 표기법으로 사용되었고, 중세까지 다른 문명들에 의해 계속 사용되었다. 현대 수학 표기법에서 이집트 분수는 단순분수와 십진소수로 대체되었다. 그러나 이집트 분수는 현대 수론과 레크리에이션 수학뿐만 아니라 고대 수학의 현대 역사 연구에서도 연구 대상이 되고 있다.

활용

이집트 분수는 역사적인 용도 외에도 분수의 다른 표현에 비해 실용적인 이점이 있다. 예를 들어, 이집트 분수는 음식이나 다른 물체를 같은 몫으로 나누는 데 도움이 될 수 있다.

예를 들어, 만약 한 사람이 피자 5판을 8명의 식객들에게 균등하게 나눠주고 싶다면, 이집트 분수로

$$\frac{5}{8} = \frac{1}{2} + \frac{1}{8}$$

이다. 4개의 피자를 8개의 반쪽으로 나누고 나머지 피자를 8개의 8분의 1로 나누는 식으로 각 식사를 하는 사람은 피자 반 개에 8분의 1을 더 받는 것을 의미한다.

비슷하게, 13개의 피자를 12명이 나누려고 할 때, 12명의 식객들에게 각각 한 개의 피자를 주고 남은 피자를 13개로 나누어 피자를 나눌 수 있다. 하지만 누군가는 아래와 같은 이집트 분수를 생각하여

$$\frac{13}{12}=\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$$

6개의 피자를 반으로 나누고, 4개를 3 등분하고, 나머지 3개를 4 등분한 다음, 각각 $1/2,\;\;1/3,\;\;1/4$씩 나눈다.

아메스 파피루스(기원전 1650년경)에서는 5부터 101까지의 모든 홀수 $n$에 대하여 $2/n$ 꼴의 분수를 단위 분수의 합으로 나타낸 수표가 있다. 예를 들면, 다음과 같다.

\begin{split}\frac{2}{13}&=\frac{1}{8}+\frac{1}{52}+\frac{1}{104}\\\frac{2}{43}&=\frac{1}{42}+\frac{1}{86}+\frac{1}{129}+\frac{1}{301}\end{split}

분수를 단위 분수의 합으로 나타내는 전통은 유럽에서 오랫동안 유지되었는데, 그리스의 헤론$^{Heron}$(130?∼75? B.C.)은 다음과 같은 기록을 남겼다.

$$\frac{25}{13}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{13}+\frac{1}{78}$$

그리고 피보나치$^{Fibonacci}$(1180?∼1250?)는 ‘산반서$^{Liber Abaci}$’(1202년)에 분수를 단위 분수로 변환하기 위한 표를 실었는데, 다음과 같은 계산도 있다.

\begin{split}\frac{98}{100}&=\frac{1}{2}+\frac{1}{4}+\frac{1}{5}+\frac{1}{50}+\frac{1}{100}\\\frac{99}{100}&=\frac{1}{2}+\frac{1}{4}+\frac{1}{5}+\frac{1}{25}\end{split}

바빌론의 분수

고대 바빌로니아인은 점토판 유물에 분수를 60진 소수로 표기한 기록을 남겼다. 소수 부분을 나타낼 때도 소수점 아래를 60을 밑으로 표현하였다. 아래 사진은 YBC7289이다. $\sqrt {2}$의 근삿값을 기록하고 있어서 유명하다.

YBC 7289 - Wikipedia

대각선에 있는 1; 24,51,10이 나타내는 수를 10진법으로 나타내면 아래와 같다. (참고: 점토판에선 ';'처럼 소수점을 나타내는 기호를 쓰지 않았다. 그냥 문맥을 보고 판단해야 한다고 한다.)

$$1+\frac{24}{60}+\frac{51}{60^2}+\frac{10}{60^3}=1.41421\dot{2}9\dot{6}\tag{1}$$

표기법의 변천

인도의 수학자 아리아브하타$^{Aryabhatta}$(c. AD 500), 브라마굽타$^{Brahmagupta}$(c. 628), 바스카라$^{Bhaskara}$(c. 1150)는 아래와 같이 분수를 표현했다.

오늘날 숫자로 바꾸면 아래와 같다.

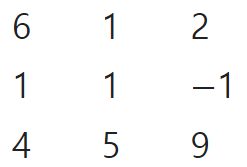
이것은 $\displaystyle{6\frac{1}{4},\;\;1\frac{1}{5},\;\;2-\frac{1}{9}=1\frac{8}{9}}$를 나타낸다.

이슬람 수학자 알-하사르$^{Al-Hassār}$는 오늘날처럼 분수막대를 사용하여 표기하였다.

분수의 종류

1. 진분수(proper fraction): 분자가 분모보다 작은 분수 

2. 가분수(improper fraction): 분자가 분모보다 큰 분수

3. 대분수(mixed fraction): 가분수를 정수와 진분수가 더해진 꼴로 표현한 분수

$$2\frac{2}{3}=2+\frac{2}{3}, \;\;2\frac{3}{4}=2+\frac{3}{4}, \cdots$$

4. 번분수(complex fraction): 분모나 분자에 분수가 있는 분수

$${\frac {\,{\dfrac {a}{b}}\,}{\dfrac {c}{d}}}={\frac {a}{b}}\div {\frac {c}{d}}={\frac {ad}{bc}}$$

5. 연분수(continued fraction): 번분수의 특별한 경우로 분모에 단위분수가 되풀이 되는 분수

$$\frac{415}{93}=4+\cfrac {1}{2+{\cfrac {1}{6+{\cfrac {1}{7}}}}}=[4;2,6,7]$$

분수를 소수로 표현

디르크 얀 슈트루이크는 소수점의 기원에 대해 다음과 같이 말한다.

일반적인 계산 관행으로서 소수점의 도입은 네덜란드 수학자 사이먼 스테빈$^{Simon Stevin}$(1548–1620)에 의해 프랑스어 번역본인 라 디스메와 함께 1585년 레이덴에서 출판된 플랑드르 팸플릿 데 티엔데(De Thiende)로 거슬러 올라갈 수 있다. 스테빈보다 수세기 전에 중국인들은 이미 10진 소수를 사용했으며, 페르시아의 천문학자 알 카슈$^{ Al-Kāshī }$는 산술 키(Key to arithmetic: 사마르칸트 15세기 초)에서 10진 소수와 60진 소수를 매우 쉽게 사용했다.

페르시아의 수학자 잠쉬드 알 카쉬$^{Jamshīd al-Kāshī}$는 15세기에 10진 소수와 60진 소수를 발견했다고 주장했지만, J. 레나르트 베르그렌은 10세기 초에 바그다드의 수학자 아부 알 하산 알 우클리디시$^{ Abu'l-Hasan al-Uqlidisi}$가 십진 소수를 5세기 전에 처음 사용했기 때문에 그가 잘못되었다고 언급했다