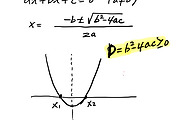
이차방정식 근을 구하는 방법
수학이야기/중학수학3 2023. 6. 7. 14:31오늘날 수학은 기호를 써서 매우 복잡한 상황을 간결한 식으로 나타낼 수 있다. 마음껏 상상력을 발휘하여 한없이 추상화되고 있다. 오늘날과 달리 아주 오래전 수학은 실제를 다루고 있다.
둘레가 20이고 넓이가 12인 직사각형은 변의 길이가 얼마인가?
방정식을 세우자.
두 변의 길이를 각각 $x,y$라고 하자.
$$2x+2y=20\Rightarrow x+y=10\tag{1}$$
$$xy=12\tag{2}$$
매우 간단한 연립방정식이라 아주 쉽게 이차방정식 $$x(10-x)=12$$을 풀면 된다.
그런데 근의 공식을 모르거나 잊었다면 어찌해야 할까?
이때 옛날 사람이 쓰던 방법이 상당히 쓸모있다.
가로와 세로의 합과 곱이 일정하다. 따라서 가로와 세로의 길이는 평균을 기준으로 같은 수를 빼고 더한 것이다. 즉, 두 수의 평균이 5이므로 가로를 $5-t$로 놓으면 세로는 $5+t$이다.
(2)에 대입하면
$$(5-t)(5+t)=12$$
$$25-t^2=12$$
$$t^2=13$$
$$t=\pm \sqrt{13}$$
아래와 같은 방정식의 근을 구해 보자.
$$x+y=p,\;\;xy=q\tag{3}$$
두 수의 평균은 $p/2$이므로 두 수는 각각 $p/2-t,\;\;p/2+t$이다.
$$\left(\frac{p}{2}-t\right)\left(\frac{p}{2}+t\right)=q$$
$$t^2=\left(\frac{p}{2}\right)^2 -q $$
$$t=\pm \sqrt{\left(\frac{p}{2}\right)^2 -q}\quad \left[\left(\frac{p}{2}\right)^2 -q \geq 0\right]$$
두 수를 구했다. $$\frac{p}{2}\pm \sqrt{\left(\frac{p}{2}\right)^2 -q}\tag{4}$$
다음 방정식을 풀어 보자.
- $x+y=8,\;\;xy=5$
- $x+y=10\;\;xy=6$
(3)을 이차방정식으로 고치면 아래와 같다.
$$x^2 -px+q=0$$
(4)를 위와 같은 이차방정식의 근을 구하는 공식으로 생각하면 된다.
예제 $3x^2 -4x-6=0$을 풀어라.
$$x^2 -\frac{4}{3}x-2=0$$
$$x=\frac{2}{3}\pm\sqrt{\left(\frac{2}{3}\right)^2-(-2)}$$
$$x=\frac{2}{3}\pm\frac{\sqrt{22}}{3}$$
다음 방정식을 풀어 보자.
- $x+y=-5,\;\;xy=-3$
- $x^2 -6x+2=0$