2024학년도 카이스트 면접문제

오래간만에 대학입시 면접문제를 본다. 중학교 문제만 보다가 고등학교 문제를 보니까 뭔가 반갑다.

문제

아래 그림과 같이 중심이 $(0,1)$이고 반지름이 $2$인 원 $X$, 중심이 $(1,0)$이고 반지름이 $1$인 원 $Y$, 중심이 $(-1,0)$이고 반지름이 $1$인 원 $ Z$가 있다. 점 $A$는 $(0,3)$에서 시작하여 원 $X$를 따라 시계 방향으로, 점 $B$는 $(1,1)$에서 시작하여 원 $Y$를 따라 시계방향으로, 점 $C$는 $(-1,1)$에서 시작하여 원 $Z$를 따라 반시계 방향으로 각각 일정한 속력으로 이동한다. 세 점 $A,B,C$가 동시에 출발하여 각 점이 원을 한 바퀴 도는데 걸리는 시간은 같다.

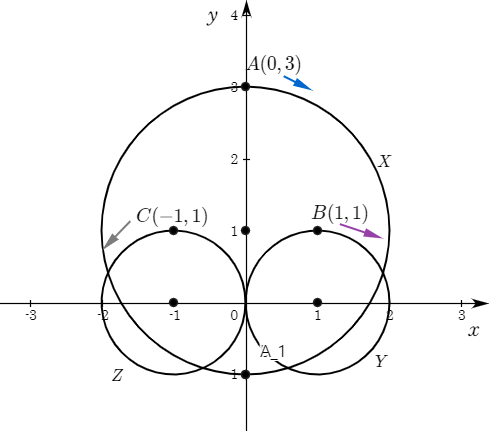
(1) 세 점 $A,B,C$가 각 원을 한 바퀴 도는 동안 한직선 위에 있는 횟수를 구하여라. (2점)

(2) 세 점 $A,B,C$가 각 원을 한 바퀴 도는 동안 만드는 삼각형 $ABC$ 넓이의 최댓값을 구하여라. (3점)

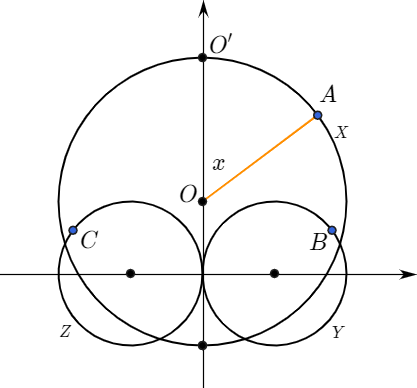
아래 그림과 같이 점 $O$의 좌표를 $(0,1)$, 점 $O^{\prime}$의 좌표를 $(0,3)$이라고 하고 $\angle AOO^{\prime}=x$라고 하자. 각 점이 원을 한 바퀴 도는데 걸린 시간이 같으므로 세 점은 아래와 같이 나타낼 수 있다.

$$A(2\sin x, \;\;2\cos x +1)$$

$$B(\sin x +1, \;\;\cos x )$$

$$C(-\sin x -1, \;\;\cos x )$$ 이때, 점들이 원을 한 바퀴 돌기 때문에 $0\leq x < 2\pi$이다.

(1) 점 $A,B,C$가 모두 한 점에서 만나는 경우는 없으므로 다음 두 가지 경우로 나누어 생각할 수 있다.

점 $A,B,C$가 모두 다른 위치에 있을 때: 두 점 $B$와 $C$는 $y$좌표가 같으므로 세 점 $A,B,C$가 한 직선 위에 있으려면 $2\cos x+1=\cos x$에서 $\cos x=-1$이다. 주어진 조건에서 만족하는 값은 $x=\pi$ 뿐이다.

점 $A,B,C$ 중 두 점이 같은 위치에 있을 때: 점 $A$와 $B$, 점 $A$와 $C$는 만날 수 없다. 점 $B$와 $C$는 $\displaystyle{x=\frac{3\pi}{2}}$일 때 만난다. 이때는 점 $A$의 위치와 상관없이 세 점이 한직선 위에 있게 된다.

정답은 2번이다.

(1)에 따라 ($\because 2\cos x+1\geq \cos$) 점 $A$의 $y$ 좌푯값이 점 $B$와 $C$의 $y$ 좌푯값 보다 항상 크거나 같다는 사실을 알 수 있다. 그러므로 삼각형 $ABC$의 넓이 $f(x)$는 다음과 같다.

$$\begin{split} f(x)&=\frac{1}{2}(\sin x+1-(-\sin x-1))(2\cos x+1-\cos x)\\&=(\sin x+1)(\cos x+1)\end{split}$$

미분하면

$$\begin{split}f^{\prime}(x)&=\cos x(\cos x+1)-(\sin x +1)(\sin x)\\&=\cos^2 x+\cos x-\sin^2 x-\sin x\\&=(\cos x -\sin x)(\cos x +\sin x +1)\end{split}$$

이다.

$\cos x-\sin x =0$일 때, $$x=\frac{\pi}{4},\;\;x=\frac{5\pi}{4}\tag{1}$$

$\cos x +\sin x+1=0$일 때, $$\cos^2 x=(-1-\sin x)^2=1+2\sin x +\sin^2 x$$

$$1-\sin^2 x=1+2\sin x +\sin^2 x$$

$$\sin x +\sin^2 x=0$$

$$\sin x=0,\;\;\sin x=-1$$

$$x=\pi,\;\;x=\frac{3\pi}{2}\tag{2}$$

각각의 경우를 계산하면 $$f(\pi)=f\bigg(\frac{3\pi}{2}\bigg)=0$$

$$f\bigg(\frac{\pi}{4}\bigg)=\frac{3}{2}+\sqrt2 ,\;\;f\bigg(\frac{5\pi}{4}\bigg)=\frac{3}{2}-\sqrt2$$

따라서 최댓값은 $3/2+\sqrt2$이다.

다른 풀이

삼각형 $ABC$의 넓이 $f(x)=(\sin x+1)(\cos x+1)$에서 시작하자.

$$(\sin x+\cos x)^2=1+2\sin x \cos x\leq 2\tag{3}$$

$$\begin{split}f(x)&=(\sin x+1)(\cos x+1)\\&=\sin x\cos x+\sin x +\cos x +1\\&=\frac{1}{2}((\sin x+\cos x)^2-1)+\sin x+\cos x +1\\&=\frac{1}{2}(\sin x +\cos x +1)^2\end{split}$$

(3)에서 $\sin x+\cos x\leq \sqrt2$이다.

따라서 $f(x)$의 최댓값은 

$\displaystyle{x=\frac{\pi}{4}}$일 때, $\displaystyle{\frac{(\sqrt2 +1)^2}{2}=\frac{3}{2}+\sqrt2}$이다. 

예시 답안으로 제시하고 있는데 다른 풀이로 접근한 학생은 많지 않을 듯 하다.