원뿔곡선
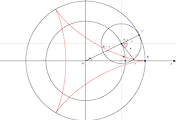
수학이야기/기하벡터 2014. 6. 11. 14:12아폴로니우스(Appolonius, B.C. 262~200)는 원뿔곡선론(conics)을 썼는데 이책에 원뿔곡선의 이름이 나온다. 타원(ellipse), 포물선(parabola), 쌍곡선(hyperbola) 그리고 원(circle)이 있다. 방정식으로 나타냈을 때 차수를 보고 2차곡선으로 부르기도 하는데 이글에선 원뿔과 평면이 만나서 생기는 곡선으로 정리해 보고자 한다.
점 $V$에서 만나는 두 직선 $A,L$이 있을 때 직선 $L$을 직선 $A$를 둘레로 회전하면 원뿔 $K$가 생긴다. 이때, $L$은 모선(generator), $A$는 축(axis), $V$는 꼭짓점(vertex), $A$와 $L$ 사이의 각 $\alpha=\angle(A,L)$를 원뿔의 반 꼭지각(half vertex)으로 부른다.
정의 1 : 평면 $H$와 두 원뿔 $K$의 교집합, $C=H \cap K$를 원뿔곡선이라고 한다.
원뿔 $K$의 축 $A$와 평면 $H$ 사이의 각을 $\beta$, 즉 $\beta=\angle(A,H)$라 하자.
정의 2 : 원뿔곡선 $C$는 $\alpha,\;\;\beta$의 관계에 따라 다음과 같이 나눈다.
(1) $\alpha < \beta \implies C$는 타원(ellipse)
(2) $\alpha = \beta \implies C$는 포물선(parabola)
(3) $\alpha >\beta \implies C$는 쌍곡선(hyperbola)
참고 : 평면이 꼭짓점 $V$를 포함할 때, 원뿔곡선 $C=H \cap K$를 퇴화 원뿔곡선이라 한다.
다음은 1822년 벨기에 수학자 단델린(G.P Dandelin)이 연구한 내용이다.
정의 3 : $S_1$과 $S_2$를 원뿔 $K$에 내접하고 평면 $H$에 접하는 구라 하자. 이때, $F_1 =S_1 \cap H$과 $F_2 =S_2 \cap H$를 원뿔곡선 $C =K \cap H$의 초점(focus)이라고 한다. 또한 $S_i \cap H=Q_i(i=1,2)$는 축과 90도인 원이고, 이 원을 포함하는 평면을 $E_i$라고 할 때, $D_i=E_i \cap H$를 원뿔곡선 $C$의 준선(directrix) 이라한다. 이때, $F_i =S_i \cap H(i=1,2)$를 준선 $D_i(i=1,2)$의 이웃초점이라 한다.
 |
 |
정리 3.1 : 만약 원뿔곡선 $C$가 타원이라면 $\forall P \;\; \in C$에 대하여 $\overline{PF_1}+\overline{PF_2}$이다.
그림에서 $R_1 =S_1 \cap K\;\;R_2 =S_2 \cap K$이므로 원이고 두 원을 품는 평면은 평행하다.
임의의 점에서 구에 접하는 접선은 모두 길이가 같다.
$\overline{PF_1}=\overline{PQ}$
$\overline{PF_2}=\overline{PT}$
$\therefore \overline{PF_1}+\overline{PF_2}=\overline{QT}$
정리 3.2 원이 아닌 원뿔곡선은 적어도 하나의 준선을 가진다.
원뿔 $K$에 내접하고 평면 $H$와 접하는 구를 $S$라고 하자.
이 때, $Q=S \cap K$이고 원 $Q$를 포함하는 평면을 $E$라고 하자.
평행하지 않은 평면은 언제나 하나의 교선을 가지므로 교선 $D=E \cap H$가 있는데 이것은 원뿔곡선 $C$의 준선이다.
원뿔곡선 $C$가 원이라면 두 평면 $E$와 $H$는 평행하므로 교선이 없다. 따라서 원은 준선이 없다.
그림에서 포물선 위 $P$를 지나는 모선 $g$가 구와 만나는 점 $Q$를 품고 원뿔 축에 수직인 평면 $E$이라고 하자.
$E$와 구가 만나는 원을 $K_1$ 포물선 위의 임의의 점 $P$를 품고 평면 $E$와 평행인 평면이 원뿔과 만나는 원을 $k_2$라고 하자.
포물선 $C$를 품은 평면 $H$와 $E$가 만나는 직선 $d$는 포물선의 준선이다.

평면 $H$와 평행인 또 다른 모선이 구와 만나는 점을 $A$, 원 $k_2$와 만나는 점을 $B$라고 하자.
$P$에서 $d$에 내린 수선의 발을 $P^{\prime}$라고 하자.
$d \bot \overline{PP^{\prime}}$
포물선 정의($\alpha =\beta$)에 의해 두 직선 $\overline{PP^{\prime}},\; \overline{PQ}$가 원뿔의 축과 이루는 각이 같다. 또한 축 위로의 정사영은 두 원 $K_1, K_2$의 중심을 잇는 선분 $\overline{O_1 O_2}$와 길이가 같다.
$\overline{O_1O_2}=\overline{PP^{\prime}}\cos \beta$이다.
$\overline{O_1O_2}=\overline{QP}\cos\alpha$이고, 접선 성질에 따라 $\overline{PQ}=\overline{PF}$이므로
$\overline{PF}=\overline{PP^{\prime}}$
$\forall P\in C$에서 준선과 초점에 이르는 거리가 같다.
정의 4 : 원뿔곡선 $C$에서 다음에 주어진 $e$ 값을 이심률(eccentricity)이라고 한다.
$$e=\frac{\cos \beta}{\cos \alpha}$$
정리 4.1 원뿔곡선 $C$는 이심률 $e$에 의해 다음과 같이 분류된다.
(1) $e=0$이면 $C$는 원
(2) $0<e<1$이면 $C$는 타원
(3) $e=1$이면 $C$는 포물선
(4) $1<e$이면 $C$는 쌍곡선
정리 4.2 원뿔곡선 $C$의 이심률이 $e$, 준선이 $D$ 그리고 $D$의 이웃초점이 $F$일 때, 임의의 점 $P\in C$에 대해서 $\overline{PF}=e\overline{PD}$이다.
 |
 |
증명 그림과 같이 임의의 점 $P\in C$의 평면 $E$위로의 정사영을 $Z$, $D$위로의 정사영을 $T$로 놓자.
$\overline{ZP} \bot E$이므로 $\overline{ZP}$는 원뿔의 축과 평행하다. 따라서 $\angle{RPZ}=\alpha, \angle{TPZ}=\beta$
$$\overline{PT}\cos \beta =\overline{PZ}=\overline{PR}\cos \alpha$$
접선 성질에 따라 $\overline{PR}=\overline{PF}$이고, $\overline{PT}=\overline{PD}$이다.
$$\overline{PF}\cos \alpha=\overline{PD}\cos \beta$$
$$\therefore\;\;\;\overline{PF}=\frac{\cos \beta}{\cos \alpha}\overline{PD}=e \overline{PD}$$
정리 4.3 원뿔곡선 $C$가 쌍곡선일 때, $\forall P \in C$에 대하여 $|\overline{PF_1}-\overline{PF_2}|=2a\;\;(a$는 상수) 이다.

증명
평면 $H$가 원뿔 $K$를 자른 곡선 $C$가 쌍곡선이라고 하자.
$C=H \cap K$
원뿔에 내접하면서 평면 $H$에 접하는 구는 그림과 같이 둘이 있다.
임의의 점 $P \in C$를 지나는 모선이 두 구와 만나는 점을 각각 $M,N$이라 하고
$M,N$을 품고 원뿔축에 수직인 평면과 원뿔이 이루는 원을 각각 $k_1, k_2$라고 하자.
접선 성질에 따라
$$\overline{PM}=\overline{PF_1},\;\;\overline{PN}=\overline{PF_2}$$
두 원 $k_, k_2$를 품은 평면은 서로 평행하므로 $|\overline {MN}|$은 일정한 값을 가진다.
$$|\overline{PF_1}-\overline{PF_2}|=|\overline{PM}-\overline{PN}|=|\overline {MN}|$$
참고 기하학 다시보기-경문사
같이 보기