수열의 극한

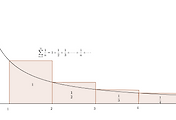
수열 $\displaystyle{a_n =\frac{1}{n}}$인 수열 $\{a_n\}$에서 $n$이 커짐에 따라 $a_n$의 값은 어떻게 달라지는지 알아보자.

$$a_{n+1}= \frac{1}{n+1} <\frac{1}{n}=a_n$$

이므로 $n$이 한없이 커지면 $a_n$은 한없이 작아진다.

그런데, $\forall n\in \mathbb{N}$에 대하여 $\displaystyle{a_n =\frac{1}{n}>0}$이므로 $a_n$은 $0$에 한없이 가까워진다.

정의 1 : 수열 $\{a_n\}$에서 $n$이 한없이 커질 때, $a_n$이 일정한 수 $L$에 한없이 가까워지면 이 수열 $\{a_n\}$은 $L$에 수렴한다고 하며, $L$을 수열 $\{a_n\}$의 극한값 또는 극한이라고 한다. 기호로는

$\displaystyle{\lim_{n\rightarrow \infty}a_n=L}$ 또는 $n\rightarrow \infty$ 일 때 $a_n \rightarrow L$

로 적는다. 수열이 수렴하지 않으면 발산한다고 한다.

여기서 '한없이 가까워진다.'는 말을 더 분명하게 하기 위해 $\epsilon$을 써서 아래와 같이 엄밀하게 정의한다.

$\forall \varepsilon >0$에 대하여 $\forall n>N(\varepsilon)\Rightarrow  |a_n -L|<\varepsilon$을 만족하는 $N(\varepsilon) \in \mathbb{N}$이 존재하면 수열 $\{a_n\}$은 $L$에 수렴한다고 하고, $L$을 수열 $\{a_n\}$의 극한값 또는 극한이라고 한다. 기호로는 

$\displaystyle{\lim_{n\rightarrow \infty}a_n=L}$ 또는 $n\rightarrow \infty$ 일 때 $a_n \rightarrow L$

로 적는다.

http://en.wikipedia.org/wiki/Limit_of_a_sequence

수열 $\displaystyle{a_n =\frac{1}{n}}$일 때, $\varepsilon >0$에 대하여 $\displaystyle{N(\varepsilon)=\big[\frac{1}{\varepsilon}\big]+1}$라고 하자. (단, $[x]$는 $x$를 넘지 않는 최대 정수)

$$\big[\frac{1}{\varepsilon}\big]+1>\frac{1}{\varepsilon}$$

$\forall n>N(\varepsilon)$에 대하여 $$\displaystyle{|a_n -0| = a_{n}=\frac{1}{n}<\frac{1}{N(\varepsilon)}= \frac{1}{[\frac{1}{\varepsilon}]+1}< \varepsilon}$$ 이다. 그러므로 $$\lim_{n\rightarrow \infty}\frac{1}{n}=0$$ 이다.

정리 수열 $\{a_n\}, \{x_n\}$가 어떤 상수 $C>0$에 대하여

$$\forall n \in \mathbb{N}, |x_n-x|\leq C|a_n|$$

을 만족하고 $a_n \rightarrow 0$이면 $x_n \rightarrow x$이다.

증명 주어진 $\varepsilon>0$에서 $a_n \rightarrow 0$이라고 하면 아래를 만족하는 자연수 $N_a (\varepsilon/C)$가 존재한다.

$$\forall n\geq N_a(\varepsilon/C),\;\;|a_n|=|a_n -0|< \frac{\varepsilon}{C}$$

$$|x_n -x|\leq C|a_n|< C\frac{\varepsilon}{C}=\varepsilon$$

$$\therefore \;\;x_n \rightarrow x$$

한편, $n\rightarrow \infty$ 일 때, $a_n \rightarrow L$은 $|a_n -L|\rightarrow 0$과 동치이다.

$$\lim_{n\rightarrow \infty}a_n=L,\;\;\lim_{n\rightarrow \infty}b_n =M$$ 이라고 하고 극한값의 성질을 알아보자.

$n\rightarrow \infty$ 일 때, $|a_n -L|\rightarrow 0,\;\;|b_n -M|\rightarrow 0$이므로

$$0<|(a_n +b_n )-(L+M)|=|(a_n -L)+(b_n -M)|\leq|a_n -L|+|b_n -M|$$ 이다.

$$|(a_n +b_n )-(L+M)|\rightarrow0$$ 이다. 마찬가지로 생각하면 아래와 같은 성질을 확인할 수 있다.

극한값의 성질 1

두 수열 $\{a_n\}$과 $\{b_n\}$이 각각 $L$과 $M$에 수렴하면 ($k$는 상수)

1. $\displaystyle{ \lim_{n\rightarrow \infty}k=k }\;$
2. $\displaystyle{ \lim_{n\rightarrow \infty}(a_n \pm b_n)=\lim_{n\rightarrow \infty}a_n \pm \lim_{n\rightarrow \infty}b_n =L\pm M}$
3. $\displaystyle{ \lim_{n\rightarrow \infty}ka_n=k\lim_{n\rightarrow \infty}a_n =kL}$
4. $\displaystyle{ \lim_{n\rightarrow \infty}(a_n b_n)=\lim_{n\rightarrow \infty}a_n \lim_{n\rightarrow \infty}b_n =LM}$
5. $\displaystyle{ \lim_{n\rightarrow \infty}\frac{a_n}{b_n}}=\frac{\displaystyle{\lim_{n\rightarrow \infty}a_n} }{\displaystyle{\lim_{n\rightarrow \infty}b_n }}=\displaystyle{\frac{L}{M}}\;\;(b_n \not=0,\;\;M \not=0)$

증명 2 $\displaystyle{ \lim_{n\rightarrow \infty}(a_n +b_n)=\lim_{n\rightarrow \infty}a_n + \lim_{n\rightarrow \infty}b_n =L+M}$임을 보이자.

$$|(a_n +b_n)-(L+M)|=|(a_n -L)+(b_n -M)|\leq |a_n -L|+|b_n -M|$$

가정에 따라 $\forall \varepsilon$에 대하여 $n\geq N_1$이면 $\displaystyle{|a_n -L|<\frac{\varepsilon}{2}}$인 $N_1$이 존재한다. 마찬가지로 $n\geq N_2$이면 $\displaystyle{|b_n -M|<\frac{\varepsilon}{2}}$인 $N_2$가 존재한다.

그러므로 $N(\varepsilon)=Max\{N_1 ,N_2\}$로 놓으면

$n\geq N(\varepsilon)$에 대하여

$$|(a_n +b_n)-(L+M)| \leq |a_n -L|+|b_n -M|<\frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon$$

다음으로 4. $\displaystyle{ \lim_{n\rightarrow \infty}(a_n b_n)=\lim_{n\rightarrow \infty}a_n \lim_{n\rightarrow \infty}b_n =LM}$임을 보이자.

$$\begin{array}{1 1}|a_n b_n -LM|&=|(a_n b_n -a_n M)+(a_n M-LM)|\\ &\leq||a_n (b_n -M)|+|(a_n -L)M|\\ &=|a_n||b_n -M|+|a_n -L||M|\end{array}$$

$a_n$은 수렴하므로 유계이다. 모든 $n$에 대하여 $|a_n|\leq K_1$인 $K_1$이 존재한다.

이제 $K=Max\{K_1 ,|M|\}$이라고 하면

$$|a_n b_n -LM|\leq K|b_n -M|+K|a_n -L|$$

이제 각각 $n\geq N_1$이면 $\displaystyle{|a_n -L|<\frac{\varepsilon}{2K}}$ , $n\geq N_2$이면 $\displaystyle{|b_n -M|<\frac{\varepsilon}{2K}}$인 $N_1 , N_2$를 찾을 수 있다. 위와 마찬가지로 $N(\varepsilon)=Max\{N_1 ,N_2\}$로 놓으면

$n\geq N(\varepsilon)$에 대하여

$$|a_n b_n -LM|\leq K|b_n -M|+K|a_n -L|\leq K \cdot \frac{\varepsilon}{2K} +K \cdot \frac{\varepsilon}{2K} =\varepsilon$$

정리5가 성립함을 보이기 위해 먼저 아래를 보이자.

$$\lim_{n\rightarrow \infty}\frac{1}{b_n}=\frac{1}{M}\;\;\;(M\not=0)$$

$\displaystyle{\alpha=\frac{1}{2}|M|}$으로 생각한다면 $n\geq N_1$에 대하여 $|b_n -M|<\alpha$인 $N_1$이 존재한다.

$$-\alpha \leq -|b_n -M|\leq|b_n|-|M|$$

$$\frac{1}{2}|M|=|M|-\alpha\leq |b_n|$$

$$\therefore\;\;\frac{1}{|b_n|} \leq\frac{2}{|M|}$$

$$\left| \frac{1}{b_n}-\frac{1}{M} \right|=\left| \frac{M-b_n}{M b_n} \right|=\frac{1}{|M b_n|}|M-b_n|\leq \frac{2}{|M|^2}|M-b_n|$$

$n\geq N_2$에 대하여 $\displaystyle{|b_n -M|<\frac{1}{2}\varepsilon |M|^2}$인 $N_2$이 존재한다.

위와 마찬가지로 $N(\varepsilon)=Max\{N_1 ,N_2\}$로 놓으면

$n\geq N(\varepsilon)$에 대하여

$$\left|\frac{1}{b_n}-\frac{1}{M}\right|\leq\varepsilon$$

아래와 같은 성질도 직관적으로 확인할 수 있다.

극한값의 성질 2

두 수열 $\{a_n\}$과 $\{b_n\}$이 각각 $L$과 $M$에 수렴하면

1. 모든 자연수 $n$에 대하여 $a_n<b_n$이면 $L<M$
2. 수열 $\{c_n\}$이 모든 자연수 $n$에 대하여 $a_n<c_n<b_n$이고 $L=M$이면 $\displaystyle{\lim_{n\rightarrow \infty}c_n=L}$이다.