무한급수의 수렴, 발산 판정법

 아래와 같이 무한수열 $\{a_n\}$의 모든 항을 순서대로 합의 기호 ($+$)로 연결한 식을 무한급수 또는 간단히 급수로 부른다. 

$$\sum_{n=1}^{\infty} a_n =a_1 +a_2 +a_3 +\cdots+a_n +\cdots$$

무한급수 $\displaystyle{\sum_{n=1}^{\infty} a_n}$에서 첫째항부터 $n$째항까지 합

$$S_n  =a_1+a_2 +a_3 +\cdots+a_n =\sum_{k=1}^{n} a_k$$

을 부분합으로 부르는데 이 또한 수열이다. 이 수열 $\{S_n\}$이 일정한 상수 $S$로 수렴하면 무한급수는 $S$에 수렴한다고 하고 극한값 $S$를 무한급수의 합 으로 부른다.

정리하면

$$\displaystyle{\sum_{n=1}^{\infty} a_n=a_1 +a_2 +a_3 +\cdots+a_n +\cdots=\lim_{n\rightarrow \infty }S_n =\lim_{n\rightarrow \infty }\sum_{k=1}^{n} a_k=S}$$

흔히 무한급수의 합을 무한히 더해 나온 값으로 말하는 이가 있는데 무한은 계속 커지고 있는 상태를 말하는데 무한히 더한다는 것은 올바른 표현이 아니다. 정의와 같이 부분합 수열이 수렴하는 값으로 생각해야 그 뜻이 또렷해진다.

$$\sum_{n=1}^{\infty}{(-1)^{n-1}}1+(-1)+1+(-1)+ \cdots+(-1)^{n-1} + \cdots$$

$\{1+(-1)\}+\{1+(-1)\}+ \cdots+\{(-1)^{n-1}\} + \cdots =0+0+\cdots=0$으로 생각하거나

$1+\{(-1)+1\}+\{(-1)+1\}+\cdots=1+0+0+\cdots=1$으로 생각하면 곤란하다.

무한급수의 합을 구하는 일은 수열의 극한값을 구하는 것과 같다. 어떤 수열은 합을 간단한 식으로 나타내기 어렵다. 이런 수열로 만든 무한급수는 수렴과 발산을 판단하기 매우 어렵다. 이를 해결하기 위해 무한급수의 수렴과  발산을 판단하는 여러 가지 판정법이 있다. 

1. 비교판정법(Comparision test)

$\forall n\in \mathbb{N}\;\;a_n \geq 0 ,\;\;b_n \geq 0 , \;\;a_n \leq b_n$라고 하면 다음이 성립한다.

1) $\displaystyle{\sum_{n=1}^{\infty} b_n}$이 수렴하면 $\displaystyle{\sum_{n=1}^{\infty} a_n}$도 수렴한다.

2) $\displaystyle{\sum_{n=1}^{\infty} a_n}$이 발산하면 $\displaystyle{\sum_{n=1}^{\infty} b_n}$도 발산한다.

증명 1) 무한급수 $\displaystyle{\sum_{n=1}^{\infty} a_n}$의 부분합 $\displaystyle{\sum_{n=1}^{m} a_n}$은 증가한다.

$\displaystyle{\sum_{n=1}^{\infty} b_n}=M$이라고 하면 $\displaystyle{\sum_{n=1}^{\infty} a_n<M}$이므로 위로 한계가 있다.

증가하는 수열이 위로는 막혀 있으므로 수렴한다. 정확하게 적는다면 $\displaystyle{\sum_{n=1}^{\infty} a_n=sup\{\sum_{n=1}^{m} a_n:m\in \mathbb{N}\}}$이다. 

아래 무한급수를 보기로 삼자.
$$\sum_{n=1}^{\infty} \frac{1}{n} =\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4} +\cdots+\frac{1}{n} +\cdots$$

이 무한급수의 부분합을 $S_n$이라고 하자. 간단한 식으로 표현하기 매우 어렵다.

따라서,

$\displaystyle{S_1 =1 ,\;\;S_2 =1+\frac{1}{2}}$

$\displaystyle{S_4 =1+ \frac{1}{2}+\big(\frac{1}{3}+\frac{1}{4}\big)>1+ \frac{1}{2}+\big(\frac{1}{4}+\frac{1}{4}\big)=1+\frac{2}{2}}$

$\displaystyle{S_8 =1+ \frac{1}{2}+\big(\frac{1}{3}+\frac{1}{4}\big)+\big(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8} \big)>1+ \frac{1}{2}+\big(\frac{1}{4}+\frac{1}{4}\big)+\big(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8} \big)=1+\frac{3}{2}}$
 $\vdots$

$\displaystyle{S_{2^n}>1+ \frac{n}{2}}$

이므로 수열 $\{S_n\}$은 발산한다. 그러므로 이 무한급수는 발산한다.

한편, $n>1$일 때, $\displaystyle{\frac{1}{n^2}<\frac{1}{(n-1)n}}=\frac{1}{n-1}-\frac{1}{n}$이므로

$\displaystyle{\sum_{n=1}^{\infty}\frac{1}{n^2}<1+\sum_{n=2}^{\infty}\frac{1}{(n-1)n}=1+\sum_{n=2}^{\infty}\big(\frac{1}{n-1}-\frac{1}{n}\big)=2}$이다.

무한급수 $\displaystyle{\sum_{n=1}^{\infty}\frac{1}{n^2}}$의 부분합은 증가하는데 위로 막혀 있으므로 수렴한다.

참고로 이 무한급수의 합은 $\displaystyle{\sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}}$이다.  증명보기

2. 극한 비교판정법(Comparision test)

모든 항이 양수인 두 무한급수 $\displaystyle{\sum_{n=1}^{\infty} a_n}$과 $\displaystyle{\sum_{n=1}^{\infty} b_n}$에 대하여

$\displaystyle{0<\lim_{n\rightarrow \infty}\frac{a_n}{b_n}<\infty}$일 때, $\displaystyle{\sum_{n=1}^{\infty} a_n}$이 수렴할 필요충분 조건은 $\displaystyle{\sum_{n=1}^{\infty} b_n}$이 수렴하는 것이다. 

증명

3. 적분 판정법(Integral test)

단조감소하는 함수 $f:[1,\infty)\rightarrow[0,\infty)$에 대하여 $\displaystyle{\int_{1}^{\infty}f(x)dx}$가 존재할 필요충분 조건은 $\displaystyle{\sum_{n=1}^{\infty}f(n)}$이 수렴이다.

증명 함수 $f$가 단조감소하므로 $j\leq x \leq j+1(j\in \mathbb{N})$이면 $f(j)\geq f(x) \geq f(j+1)$이다.

따라서

$$\int_{1}^{n}f(x)dx=\sum_{j=1}^{n-1}\int_{j}^{j+1}f(x)dx \geq \sum_{j=1}^{n-1}\int_{j}^{j+1}f(j+1)dx =\sum_{j=2}^{n}f(j)dx $$

$$\int_{1}^{n}f(x)dx=\sum_{j=1}^{n-1}\int_{j}^{j+1}f(x)dx \leq \sum_{j=1}^{n-1}\int_{j}^{j+1}f(j)dx =\sum_{j=1}^{n-1}f(j)dx $$

이다. 따라서 $\displaystyle{\sum_{n=1}^{\infty}f(n)}$이 수렴할 필요충분 조건은 $\displaystyle{\lim_{n\rightarrow \infty}\int_{1}^{n}f(x)dx}$가 수렴하는 것이다. 즉, $\displaystyle{\int_{1}^{\infty}f(x)dx}$가 존재하는 것이다.

위에 있는 무한급수를 다시 살펴보자.

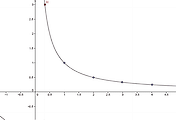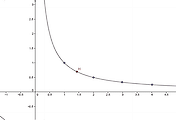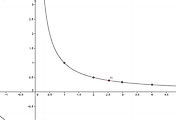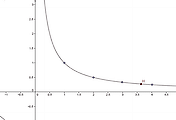
$\displaystyle{\sum_{n=1}^{\infty} \frac{1}{n}}$은 아래와 같은 사각형 넓이의 합으로 생각할 수 있다.

구분구적법을 생각해보면

$\displaystyle{\int_{1}^{n+1}\frac{1}{x}dx<\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}}$

$\displaystyle{\lim_{n\rightarrow \infty}\int_{1}^{n+1}\frac{1}{x}dx=\lim_{n\rightarrow \infty}\ln(n+1)=\infty}$이므로 이 무한급수는 발산한다.

 

아래 그림에서는 무한급수 $\displaystyle{\sum_{n=1}^{\infty} \frac{1}{n^2}}$은 수렴함을 알 수 있다.

적분판정법으로 무한급수 $\displaystyle{\sum_{n=1}^{\infty}\frac{1}{n^p}}$가 수렴할 필요충분 조건은 $p>1$임을 알 수 있다.

4. 비율판정법(ratio test)

$\forall n\in \mathbb{N}\;\;a_n >0 $인 무한급수 $\displaystyle{\sum_{n=1}^{\infty}a_n}$에 대하여

1. $\displaystyle{\rho=\lim_{n\rightarrow \infty}\frac{a_{n+1}}{a_n}<1}$이면 무한급수 $\displaystyle{\sum_{n=1}^{\infty}a_n}$ 수렴한다.

2. $\displaystyle{\rho=\lim_{n\rightarrow \infty}\frac{a_{n+1}}{a_n}>1}$이면 무한급수 $\displaystyle{\sum_{n=1}^{\infty}a_n}$ 발산한다.

증명 $\displaystyle{0<\rho=\lim_{n\rightarrow \infty}\frac{a_{n+1}}{a_n}<1}$이라고 하자.

$\rho<r<1$인 실수 $r$을 고르면 자연수 $N$이 존재하여 $\forall n\geq N\;\;(n\in \mathbb{N}$)인 $n$에 대하여 $\displaystyle{\frac{a_{n+1}}{a_n}<r}$을 만족한다.

다시 적으면 $\displaystyle{\frac{a_{N+1}}{a_N}<r}$이므로

$\displaystyle{a_{N+1}<r{a_N}}$이다. $r$을 곱하여 정리하면

$a_{N+2}<ra_{N+1}<r^2 a_N$

$a_{N+3}<ra_{N+2}<r^3 a_N$

$\vdots$

$a_{N+m}<ra_{N+m-1}<r^m a_N$

$a_{N+1}+a_{N+2}+a_{N+3}+\cdots+a_{N+m}<a_N (r+r^2 +\cdots+r^m)$

$0<r<1$이므로 오른쪽 수열은 수렴한다.

따라서, $\displaystyle{\sum_{n=N+1}^{\infty}a_n}$은 수렴한다. 유한 개 항을 더한 무한급수도 당연히 수렴한다.

$\displaystyle{\sum_{n=1}^{\infty}a_n=\sum_{n=1}^{N}a_n+\sum_{n=N+1}^{\infty}a_n}$

마찬가지 방법으로 두 번째 경우도 증명할 수 있다.