 ko
ko 월드컵 공은 둥글지 않다_텔스타 18
수학이야기 2018. 6. 28. 11:19축구 보다가 수학 공부를 한다. 올해 월드컵에 쓰는 공은 '텔스타 18'이다. 1970년 멕시코 월드컵에서 썼던 공과 이름이 같다. 텔스타는 '텔레비젼(Television)'과 '별(star)'이 더해진 말이다. 처음으로 인공위성으로 중계 방송을 시작하게 됨을 기리기 위해 붙인 이름이다. 아디다스에서 만든 텔스타는 정이십면체를 깍아서 12개 정오각형과 20개 정육각형을 면으로 가진 32면체다. 흑백 시대였던 그 시절 정오각형에는 검은 색을 넣어 눈에 확 띄는 디자인으로 바람을 일으켰다.
 |
 |
 |
 |
이름이 같으니 당연히 디자인도 같을 것으로 생각했는데 올해 쓰는 공은 가죽 여섯 조각을 이어 붙여서 만든다고 한다. 저 복잡한 조각을 어떻게 만들었을까 궁금하지 않은가? 검색하면 다 나올 줄 알았는데 잘 찾아지지 않는다. 구면 테셀레이션과 연관 있을 것으로 생각하고 위키백과를 뒤져 보니 알겠다.
정육면체를 깎거나 늘려서 만든 'Rhombicuboctahedron'을 바탕으로 만들었다.
 |
 |

그림으로는 쉽지만 아주 간단하지는 않다. 먼저 모든 면이 합동인 마름모로 만들어진 12면체(Rhombic dodecahedron)와 정6면체를 더해서 만든다.

그림에서 빨간 정사각형은 그대로 두고 파란 정사각형은 2등분 노란 정삼각형은 3등분된 부분이 포함된 다각형을 이어서 만든다.
 |
 |
위키백과에 있는일부분을 우리말로 옮겨 본다.
아르키메데스 입체는 13개다.(elongated square gyrobicupola는 세지 않고 거울에 비친 모양인 켤레( enantiomorphs) snub cube and snub dodecahedron까지 따로 세면 15개다.)
어떤 꼭짓점에서 만나는 정다각형의 꼭짓점 모양(vertex conf) 은 아래 그림과 같다. 보기를 들면 vectec conf(4,6,8)은 한 꼭짓점에서 정사각형, 정육각형 그리고 정팔각형이 만난다.(차례는 시계방향을 따른다,).
| Name (Alternative name) |
Schläfli Coxeter |
Transparent | Solid | Net | Vertex conf./fig. |
Faces | Edges | Vert. | Volume (unit edges) |
Point group |
Sphericity | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| truncated tetrahedron | t{3,3} |
 |
 |
3.6.6 |
8 | 4 triangles 4 hexagons |
18 | 12 | 2.710576 | Td | 0.7754132 | |
| cuboctahedron (rhombitetratetrahedron) |
r{4,3} or rr{3,3} |
 |
 |
 |
3.4.3.4 |
14 | 8 triangles 6 squares |
24 | 12 | 2.357023 | Oh | 0.9049973 |
| truncated cube | t{4,3} |
 |
 |
3.8.8 |
14 | 8 triangles 6 octagons |
36 | 24 | 13.599663 | Oh | 0.8494937 | |
| truncated octahedron (truncated tetratetrahedron) |
t{3,4} or tr{3,3} |
 |
 |
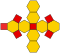 |
4.6.6 |
14 | 6 squares 8 hexagons |
36 | 24 | 11.313709 | Oh | 0.9099178 |
| rhombicuboctahedron (small rhombicuboctahedron) |
rr{4,3} |
 |
 |
3.4.4.4 |
26 | 8 triangles 18 squares |
48 | 24 | 8.714045 | Oh | 0.9540796 | |
| truncated cuboctahedron (great rhombicuboctahedron) |
tr{4,3} |
 |
 |
4.6.8 |
26 | 12 squares 8 hexagons 6 octagons |
72 | 48 | 41.798990 | Oh | 0.9431657 | |
| snub cube (snub cuboctahedron) |
sr{4,3} |
 |
 |
3.3.3.3.4 |
38 | 32 triangles 6 squares |
60 | 24 | 7.889295 | O | 0.9651814 | |
| icosidodecahedron | r{5,3} |
 |
 |
3.5.3.5 |
32 | 20 triangles 12 pentagons |
60 | 30 | 13.835526 | Ih | 0.9510243 | |
| truncated dodecahedron | t{5,3} |
 |
 |
3.10.10 |
32 | 20 triangles 12 decagons |
90 | 60 | 85.039665 | Ih | 0.9260125 | |
| truncated icosahedron | t{3,5} |
 |
 |
5.6.6 |
32 | 12 pentagons 20 hexagons |
90 | 60 | 55.287731 | Ih | 0.9666219 | |
| rhombicosidodecahedron (small rhombicosidodecahedron) |
rr{5,3} |
 |
 |
3.4.5.4 |
62 | 20 triangles 30 squares 12 pentagons |
120 | 60 | 41.615324 | Ih | 0.9792370 | |
| truncated icosidodecahedron (great rhombicosidodecahedron) |
tr{5,3} |
 |
 |
4.6.10 |
62 | 30 squares 20 hexagons 12 decagons |
180 | 120 | 206.803399 | Ih | 0.9703127 | |
| snub dodecahedron (snub icosidodecahedron) |
sr{5,3} |
 |
 |
3.3.3.3.5 |
92 | 80 triangles 12 pentagons |
150 | 60 | 37.616650 | I | 0.9820114 | |
준정다면체(semiregular polyhedron)의 정의는 하나 이상의 모양을 포함하고 있다. 마름모 12면체를 잡아 늘인 다면체(elongated square gyrobicupola or "pseudo-rhombicuboctahedron")