데카르트 곡선 $x^3 +y^3 -3axy=0$

1596. 3. 31.은 데카르트가 생일이다. 프랑스 중부 작은 마을에서 태어났고 1650. 2. 11.에 스톡홀름에서 죽었다. 8살 때부터 예수회 학교에서 공부를 시작했는데 몸이 상당히 병약해서 다른 학생들과 달리 오전 11시까지 침대에 있을 수 있었다. 훗날 생애내내 습관이 되었는데 1649년 스웨덴 여왕 크리스티나가 날마다 새벽 5시에 접선을 그리는 법을 가르치러 오게 하는 바람에 습관을 지키지 못하게 되었다. 몇 달 동안 차가운 스웨던 날씨에 왕궁을 산책하다가 얻은 감기로 세상을 떠나게 되었다고 전해지지만 약물중독으로 죽었다는 이야기도 있다. 데카르트는 파리에 있는 교회에 묻혔다.

현대 수학은 두 가지 기초 위에 있다. 하나는 뉴턴이 남긴 미적분이고 다른 하나는 데카르트가 남긴 기하 Geometry와 대수 Algebra를 통합하는 해석기하다. 발전된 해석기하에 관한 개념은 어떤 학자들이 현대 수학의 생일로 일컫는 1619. 11. 10.에 데카르트로부터 나왔다. 데카르트는 아리스토텔레스의 논리와 관련한 인식론에 다년간 회의와 의문을 품고 있었다. 그는 오로지 수학이 진리를 찾는 확실하고 만족스러운 방법임을 느꼈다. 데카르트 철학은 과학적 방법이 태어나게 만들었다. 

1638년 처음으로 데카르트는 페르마의 극값을 찾는 기술에 도전하다가 찾아낸 곡선에 대하여 언급했다. 임의의 점에서 접선을 찾는 문제를 두고 페르마에게 도전했다. 곧바로 쉽게 해결한 페르마에 비해 해내지 못한 데카르트는 매우 원통해 했다. 라틴어 이름은 나뭇잎 leaf을 뜻하는 folium이다. 아래와 같이 그래프가 나뭇잎을 닮았다. 프랑스말로는 리본의 매듭 noeud de ruban으로 독일말로는 데카르트 시트 kartesisches Blatt로 부른다. 방정식과 그래프는 아래와 같다. 1966년 알바니아에서 이 곡선을 그려넣은 우표를 발행하기도 했다.

$$x^3 +y^3 -3axy=0\quad\quad a>0\tag{1}$$

$$x=r\cos\theta,\quad\quad y=r\sin\theta\tag{2}$$

(2)로 (1)을 정리하여 직교방정식을 극방정식으로 바꾸면 아래와 같다.

$$(r\sin\theta)^3+(r\cos\theta)^3=3a r\sin\theta \cdot r \cos \theta$$

$$r=\frac{3a \sin\theta \cos\theta}{\sin^3 \theta + \cos^3 \theta}\tag{3}$$

이식을 변형해 보자.

$$r=\frac{3a \tan\theta \sec\theta}{1+\tan^3\theta}$$

$$r^2=\frac{9a^2 \tan^2 \theta \sec^2 \theta}{(1+\tan^3\theta)^2}=\frac{9a^2 \tan^2 \theta (1+\tan^2 \theta)}{(1+\tan^3\theta)^2}$$

여기서 $\tan \theta=t$로 치환하자.

$$r^2=\frac{9a^2 t^2( 1+t^2)}{(1+t^3)^2}$$

이 곡선은 $t=-1$에서 불연속이다. $-1<t<0$일 때는 왼쪽 날개, $0<t$일 때는 고리,  $t<-1$일 때는 오른쪽 날개 부분이 그려진다. $\tan \theta=-1$에서 $\theta=- \pi/4$이므로 점근선은 기울기가 $-1$이다. 실제로 점근선은 $y=-x-a$이고 (3)을 (2)에 넣어서 정리하고 변수 $t=\tan \theta$를 매개변수로 하여 나타내면 아래와 같다.

$$x(t)=\frac{3at}{1+t^3}\quad\quad y(t)=\frac{3at^2}{1+t^3}\tag{4}$$

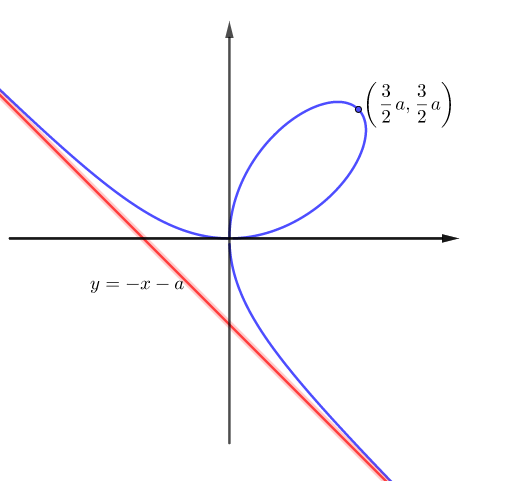
고리 안에 넓이를 구해보자. 먼저 극방정식으로 주어진 곡선의 넓이는 아래와 같다.

$$A=\int_{0}^{\pi/2} \frac{1}{2}r^2 d \theta\tag{5}$$

여기서 $\theta=\tan^{-1}t$이므로 $\displaystyle{d\theta=\frac{dt}{1+t^2}}$이다.

(5)을 위와 같이 치환하여 적분하자.

$$A=\int_{0}^{\infty} \frac{1}{2}\frac{(3at)^2 (1+t^2)}{(1+t^3)^2}\frac{dt}{1+t^2}=\frac{3}{2}a^2\int_{0}^{\infty}\frac{3t^2 dt}{(1+t^3)^2}$$

다시 $1+t^3=u$로 치환하면 $3t^2 dt=du$이므로

$$A=\frac{3}{2}a^2 \int_{1}^{\infty}\frac{du}{u^2} =\frac{3}{2}a^2 \bigg[-\frac{1}{u} \bigg]_{1}^{\infty}=\frac{3}{2}a^2 $$

 

https://en.wikipedia.org/wiki/Folium_of_Descartes

Folium of Descartes - Wikipedia

https://mathworld.wolfram.com/FoliumofDescartes.html

Folium of Descartes -- from Wolfram MathWorld