또 다른 오일러 상수

오일러 이름이 붙은 상수 자연 로그의 밑인 $e$는 널리 알려져 있다. 또 다른 오일러 상수 $\gamma$가 있다. 오일러-마스케로니 상수로도 부른다. 아마도 자기 이름이 붙은 상수를 둘이나 가진 수학자는 오일러가 유일하지 않을까?

오일러 상수 $\gamma$는 아래에 있는 수열 $\{a_n\}$의 극한값이다.

$$a_n=\sum_{k=1}^{n} \frac{1}{k}-\ln n$$

이 수열은 아래 그림과 같이 조화수열과 자연로그의 차를 나타낸다.

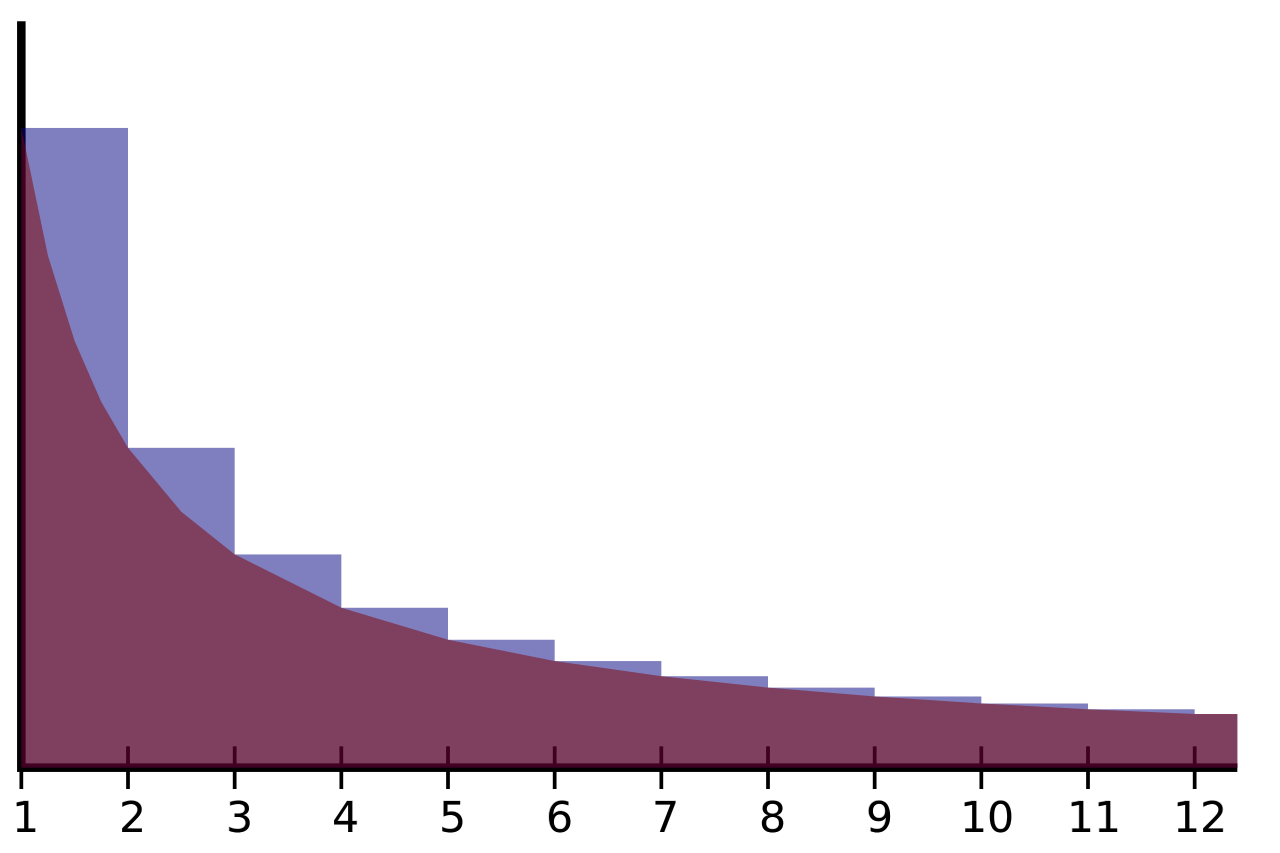
역사

이 수열은 1734년 스위스 수학자 오일러가 쓴 <조화수열에 대한 고찰>에 처음 등장한다. 오일러는 $C$나 $O$로 표시하였다. 1790년 이탈리아 수학자 마스케로니Lorenzo Mascheroni는 $A$와 $a$로 적었다. 세월이 흐른 뒤 이 상수가 감마 함수 gamma function와 아주 관계가 깊다는 사실을 발견한 수학자들이 $\gamma$로 적기 시작했다. 예) 독일 수학자 브레트슈나이더 Carl Anton Bretschneider 와 영국 수학자 드모르간 Augustus De Morgan이 있다.

마침 연습문제에 이 상수를 다루고 있는 문제가 있으니 살펴 보기로 하자.

https://en.wikipedia.org/wiki/Euler-Mascheroni_constant

Euler–Mascheroni constant - Wikipedia