그래프와 행렬

이산수학(discrete mathematics)에 있던 그래프가 수학1로 옮겨 왔다. 아주 간단한 것들이지만 이산수학에서 출제되던 복잡한 문제가 나온다면 그렇게 쉽다고 볼 수도 없다. 물론 처음이니까 아주 어려운 것은 나오지 않을 것이라 믿는다. 어느 정도 범위까지 공부해야 할까? EBS 수능완성을 보니 교과서 내용만 하기엔 조금 불안한다. 그래프 이론을 조금 더 정리해 둔다.

그래프란?

쉽게 말하면 아래와 같이 점을 선으로 연결한 것이다. 그래프 $G$는 꼭짓점(vertex or node)들의 집합 $V$와 변(edge or line)들의 집합 $E$로 이루어졌다. 수학에선 $G=(V,E)$와 같이 쓴다. 

위 그래프는 꼭짓점 6개, 변 7개로 이루어졌다.

$V= \{1, 2, 3, 4, 5, 6\}, E=\{(1, 2), (1, 5), (2, 3), (2, 5), (3, 4), (4, 5), (4, 6)\}$이다.

변에 방향이 있어 화살표로 표현되면 방향 그래프(directed graph) 방향이 없으면 무방향 그래프(undirected graph)라고 하는데 무방향 그래프만 다룬다. 자기 자신으로 되돌아 오는 변을 루프(loop)라고 하고 같은 두 꼭짓점을 공유하는 변은 평행하다고 부른다. 어떤 꼭짓점도 루프를 가지지 않으며 연결된 두 꼭짓점은 단 하나의 변만 있는 그래프를 단순(simple) 그래프라고 부른다. 임의의 두 꼭짓점이 모두 단 하나의 변으로 연결된 그래프를 완전(complete) 그래프라고 부른다. 꼭짓점이 $n$개인 완전그래프를 $K_{n}$이라고 쓰는데 변의 개수는 ${}_n C _{2}$ 이다.

고등학교 수학1에서는 단순그래프를 행렬로 바꾼 것을 주로 다룬다. 별다른 말이 없으면 단순 무방향 그래프를 이야기하는 것이다. 꼭짓점이 $n$개인 그래프를 성분 $a_{ij}$가 꼭짓점 $i$에서 $j$로 변이 연결되어 있으면 $1$ 아니면 $0$인 $n$차 행렬로 나타낸다.

그래프를 나타내는 행렬의 성질

단순 무방향 그래프는 대각선이 모두 $a_{i i} =0$이고 $a_{ij} =a_{ji}$인 대칭행렬로 나타난다. 한 꼭짓점에 연결된 변의 개수를 차수(degree)라고 하는데 각 행의 수를 더하면 꼭짓점의 차수가 된다. 또한 모든 성분을 더하면 변의 개수의 2배가 된다.

다시 말해 꼭짓점들의 차수를 모두 더하면 늘 2의 배수 다시 말해 짝수가 된다.

정리 1. 그래프에서 홀수 차수인 꼭짓점은 언제나 짝수개이다.

예를 들어 꼭짓점이 5개인 그래프 가운데 차수가 4, 3, 3, 2, 1 인 그래프는 없다. 홀수 차수인 꼭짓점이 3이기 때문이다. 그래프를 그리기에 앞서 차수들의 합을 구하고 이를 2로 나누어 변의 개수를 적어두고 그리면 쉽게 그릴 수 있다. 또한 꼭짓점 개수가 $n$개인 모든 그래프를 찾을 때에도 쓸모 있는 정리이다. 꼭짓점이 1,2,3,4개인 그래프를 모두 그리면 아래와 같다.

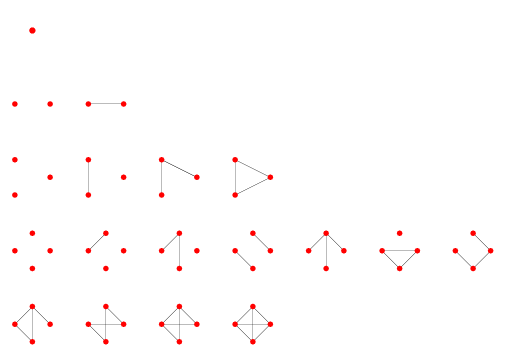
이 가운데 꼭짓점 개수가 4인 경우를 살펴보자. 변이 가장 많은 완전그래프가 변이 ${}_4 C _{2} =6$ 개이므로 변의 개수는 $0, 1, 2, 3, 4, 5, 6$이고 꼭짓점 차수 합은 각각 $0, 2, 4, 6, 8, 10, 12$이다.

변의 개수에 따라 꼭짓점 차수를 적어보자.  꼭짓점이 4 이므로 3차가 최고 차수이고 홀수점은 짝수개 있어야 한다. 아래와 같이 3을 기준으로 대칭 구조를 이루고 있다.

변이 0개 일 때, (0 0 0 0)

변이 1개 일 때, (1 1 0 0)

변이 2개 일 때, (2 1 1 0), (1 1 1 1)

변이 3개 일 때, (3 1 1 1), (2 2 2 0), (2 2 1 1)

변이 4개 일 때, (1 2 2 3), (2 2 2 2)

변이 5개 일 때, (2 2 3 3)

변이 6개 일 때, (3 3 3 3)

해밀턴 경로와 오일러 회로

그래프는 컴퓨터나 전기회로를 만들 때 각 점들은 어떻게 가장 효율적으로 연결할 것인가를 따지는 데 사용한다. 배달하는 이들이 어떻게 최적화된 경로를 찾을 것인가도 그래프를 써서 찾을 수 있다. 이런 문제를 해결하는데 쓰는 해밀턴 경로와 오일러 회로를 알아보자.

꼭지점들을 변들을 따라 이어 나간 것을 경로(path)라고 부르고 제자리로 다시 돌아오는 경로는 회로(cycle or circuit)이라고 부른다. 모든 꼭짓점들을 딱 한 번만 거치는 경로를 해밀턴 경로(Hamilton path)라고 한다. 출발점으로 다시 돌아올 수 있으면 해밀턴 회로라고 부른다. 모든 변들을 딱 한 번 지나는 경로를 오일러 경로라고 하고 제자리로 다시 돌아올 수 있다면 오일러 회로라 부른다. 

오일러 회로는 한붓 그리기 문제와 같다. 쾨니히스베르크 다리 문제에서 시작되었다. 해밀턴 회로는 대표적인 NP-complete 문제인 우편 배달부 문제와 관련되어 있다.

정리 2 모든 꼭짓점의 차수가 꼭짓점 개수의 반보다 크거나 같으면 해밀턴 회로를 가진다. 디랙의 정리(1952) 꼭짓점이 $n$개라면 임의의 꼭짓점 $V_i \in V$에 대하여 $$\frac{n}{2}\leq \deg(V_i)$$이면 해밀토니안이다.

오일러 경로는 홀수 차수를 갖는 점이 없거나 2개라야 존재하고 오일러 회로는 홀수 차수인 꼭짓점이 없어야 존재한다.