평행선은 무엇인가?

같은 평면에 놓여있는 서로 다른 두 직선은 만나거나 만나지 않는다. 두 직선 $l$과 $m$이 만나지 않을 때 두 직선은 평행이라고 한다. 기호로는 $$l // m$$이다. 중학교 아니 초등학생도 평행선은 서로 만나지 않는 직선을 일컫는다는 것을 알고 있다. 하지만 두 직선이 만나는지 안 만나는지 어떻게 확인해야 하냐고 물으면 시원한 대답이 잘 나오지 않는다.

직선은 끝이 없다. 두 직선을 한없이 늘려도 만나지 않아야 평행이다. 그러나 무한하게 늘릴 수는 없다. 따라서 일부분만 보고 두 직선이 평행인지 아닌지 판단해야 한다. 그래서 유클리드 원론은 평행선 공준을 아래와 같이 다소 복잡하게 적고 있다. (참고: 공준은 오늘날 공리로 부르는데 증명하지 않고 참으로 받아들이는 명제이다. 이들 공준으로부터 이끌어낸 참인 명제를 정리라고 부른다.)

평행선 공준
두 직선이 다른 직선과 만날 때, 두 직선을 한없이 늘리면 같은 쪽에 있는 안쪽 각을 더해서 직각 둘보다 작은 쪽에서 만난다. 

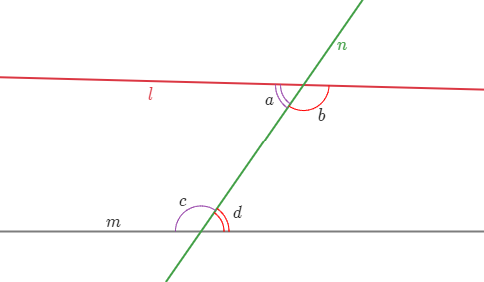
요즘 표현으로 말하면 직각 둘은 180도이다. 아래 그림에서 $\angle b+\angle d<180^{\circ}$라면 두 직선 $l$과 $m$을 오른쪽으로 한없이 늘리면 서로 만난다. 이제 우리는 무한히 늘려 보지 않고도 두 직선이 평행인가 아닌가를 알 수 있게 되었다.

다섯째 공준인 평행선 공준은 다른 공준과 달리 간결하지 않다. 훗날 이 공준은 다른 공준들로 증명할 수 있는 정리가 아닐까 생각한 이들이 있었다. 평행선 공준을 정리로 바꾸기 위해 수많은 수학자가 증명을 시도했다. 그 과정에서 평행선 공준과 동치인 정리들을 찾았다. 그 가운데 몇 가지를 살펴보자. 중학교 교과서에선 보통 '공준'과 '정리'를 '성질'이라고 적는다.

평행선 공준을 바꿔 말하면 같은 쪽에 있는 안쪽 각을 더해서 180도가 된다면 두 직선은 어느 쪽에서도 만나지 않으므로 평행이 된다. 아래 그림에서 두 직선 $l$과 $m$이 평행이면

$$\angle b+\angle d=\angle a+\angle c=180^{\circ}$$

이다. $\angle a +\angle b=180^{\circ}$이므로

$$\angle a +\angle b=\angle b+ \angle d$$

$$\therefore \;\;\angle a=\angle d$$

또한, 맞꼭지각이므로 $\angle a= \angle e$이다.

다시 정리하면 평행인 두 직선이 다른 직선과 만날 때 생기는 엇각과 동위각은 서로 같다. 따라서 두 직선과 만나는 한 직선이 주어졌을 때 아래와 같은 성질이 있다.

1. 두 직선이 평행이면 엇각이 서로 같고, 엇각이 같으면 두 직선은 서로 평행이다.
2. 두 직선이 평행이면 동위각이 서로 같고, 동위각이 같으면 두 직선은 서로 평행이다.

 

아래 그림과 같이 꼭짓점 $A$를 지나고 변 $BC$에 평행한 직선을 긋는다. 평행이면 엇각이 서로 같으므로 삼각형의 내각을 모두 더한 값은 $180^{\circ}$임을 간단하게 보일 수 있다.

3. 삼각형의 내각을 모두 더하면  $180^{\circ}$이다.

유클리드 기하를 알면 알 수록 평행선 공준이 매우 중요함을 깨닫게 된다. 유클리드 기하는 평행선만 제대로 알면 끝난다고 할 수 있다.

증명에 나섰던 이들이 증명은 찾지 못하고 찾아낸 기하학이 바로 비-유클리드 기하학(Non-Euclidean geometry)이다. 직선과 그 위에 있지 않은 한 점이 주어졌을 때, '직선 위에 있지 않은 한 점을 지나고 주어진 직선과 평행인 직선은 단 하나 그을 수 있다.'도 평행선 공준과 같은 말이다. 이때 "단 하나"를 '없다'거나 '무수히 많다'로 바꾸어서 증명을 시도한 수학자들이 있었다. 결론을 부정해서 모순을 찾아내는 귀류법을 쓰려고 한 것이다. 모두 증명에 실패했다. 하지만 그 과정에서 평행선 공준을 '평행선을 그을 수 없다.'로 하거나 '평행선을 무수히 많이 그을 수 있다.'로 바꾸어도 모순이 없는 새로운 체계를 만들 수 있음을 알아냈다. 바로 '타원 기하'와 '쌍곡 기하'이다.

유클리드 원론 자세히 보기: https://suhak.tistory.com/153 

원론(Euclid's Elements) 1권