원과 접선

원의 접선은 중심과 접점을 잇는 직선과 수직이다.

왜 그럴까? 중학교 3학년에서 아래와 같은 성질을 배운다.

원에서 현을 수직이등분하는 직선은 중심을 지난다.
원의 중심에서 현에 내린 수선은 그 현을 이등분한다.

위와 같은 성질을 배운 다음에는 아래 그림과 같이 반지름에 수직인 현을 계속 긋다가 접선이 된다고 생각하면 된다. 하지만 이 성질을 배우지 않은 학생에게는 어떻게 설명해야 할까?

접선의 성질

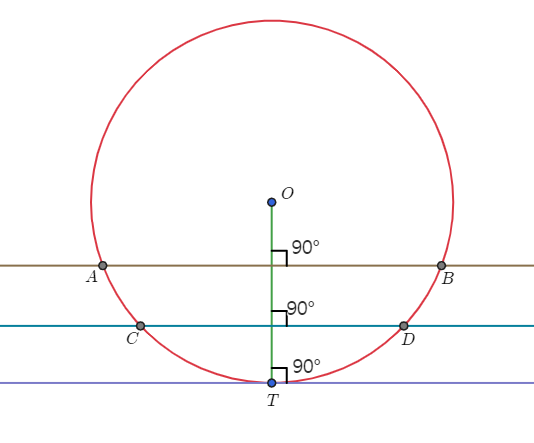
접선과 반지름

중심이 $O$인 원 위에 있는 점 $T$를 지나고 직선 $OT$와 수직인 직선이 있다고 하자. 아래 그림과 같이 직선 위에 있는 모든 점을 잇는 선분은 모두 $\overline{OT}$보다 길이가 더 길다. 따라서 점 $T$를 제외한 직선 위에 있는 모든 점은 원의 바깥에 있다. 따라서 주어진 직선은 접선이다.

원 위에 있는 점을 지나고 그 점과 중심을 잇는 반지름과 수직인 직선은 원과 한 점에서 만난다.

중심 $O$인 원이 있다. 원 위의 점 $A$를 지나는 직선이 직선 $OA$와 수직이 아니라고 하자. 선분 $OA$와 이루는 각 가운데 한 쪽은 그림과 같이 예각이다. 중심과 직선까지 거리는 점 $O$에서 직선에 내린 수선의 발 $H$와 사이의 거리이다. 아래와 같은 관계가 성립한다.

$$\overline{OA}>\overline{OH}$$

따라서 점 $H$는 원 내부에 있는 점이다. 그러므로 주어진 직선은 반드시 원과 $A$와 다른 점 $B$에서 만난다. 

원 위에 있는 점을 지나고 그 점과 중심을 잇는 반지름과 수직이 아닌 직선은 원과 서로 다른 두 점에서 만난다.

접선의 길이

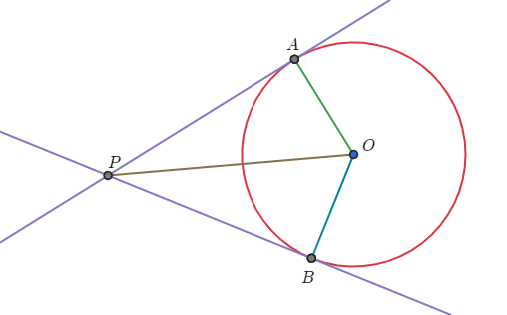
원 밖에 있는 한 점에서 원으로 접선을 두 개 그을 수 있다. 그림에서 점 $P$와 접점 $A, B$ 사이의 거리를 접선의 길이라고 한다. 이때 두 접선은 서로 길이가 같다.

$$\overline{OA}=\overline{OB}\tag{반지름}$$

$$\overline{PO}\tag{공통}$$

$$\angle OAP= \angle OBP= 90^{\circ}\tag{접선의 성질}$$

$$\triangle OPA \equiv \triangle OPB\tag{RHS합동}$$

$$\overline{PA}=\overline{PB}$$