원주각의 성질

원의 접선은 중심과 접점을 잇는 직선과 수직이다.

왜 그럴까? 중학교 3학년에서 아래와 같은 성질을 배운다.

원에서 현을 수직이등분하는 직선은 중심을 지난다.
원의 중심에서 현에 내린 수선은 그 현을 이등분한다.

위와 같은 성질을 배운 다음에는 아래 그림과 같이 반지름에 수직인 현을 계속 긋다가 접선이 된다고 생각하면 된다. 하지만 이 성질을 배우지 않은 학생에게는 어떻게 설명해야 할까?

접선의 성질

접선과 반지름

중심이 $O$인 원 위에 있는 점 $T$를 지나고 직선 $OT$와 수직인 직선이 있다고 하자. 아래 그림과 같이 직선 위에 있는 모든 점을 잇는 선분은 모두 $\overline{OT}$보다 길이가 더 길다. 따라서 점 $T$를 제외한 직선 위에 있는 모든 점은 원의 바깥에 있다. 따라서 주어진 직선은 접선이다.

원 위에 있는 점을 지나고 그 점과 중심을 잇는 반지름과 수직인 직선은 원과 한 점에서 만난다.

중심 $O$인 원이 있다. 원 위의 점 $A$를 지나는 직선이 직선 $OA$와 수직이 아니라고 하자. 선분 $OA$와 이루는 각 가운데 한 쪽은 그림과 같이 예각이다. 중심과 직선까지 거리는 점 $O$에서 직선에 내린 수선의 발 $H$와 사이의 거리이다. 아래와 같은 관계가 성립한다.

$$\overline{OA}>\overline{OH}$$

따라서 점 $H$는 원 내부에 있는 점이다. 그러므로 주어진 직선은 반드시 원과 $A$와 다른 점 $B$에서 만난다. 

원 위에 있는 점을 지나고 그 점과 중심을 잇는 반지름과 수직이 아닌 직선은 원과 서로 다른 두 점에서 만난다.

접선의 길이

원 밖에 있는 한 점에서 원으로 접선을 두 개 그을 수 있다. 그림에서 점 $P$와 접점 $A, B$ 사이의 거리를 접선의 길이라고 한다. 이때 두 접선은 서로 길이가 같다.

$$\overline{OA}=\overline{OB}\tag{반지름}$$

$$\overline{PO}\tag{공통}$$

$$\angle OAP= \angle OBP= 90^{\circ}\tag{접선의 성질}$$

$$\triangle OPA \equiv \triangle OPB\tag{RHS합동}$$

$$\overline{PA}=\overline{PB}$$  

원주각의 성질

현은 원둘레 위에 있는 서로 다른 두 점을 잇는 선분이다. 활꼴은 현과 호로 이루어진 도형이다. 현은 아래 그림과 같이 원을 두 개의 활꼴로 나눈다. 이때 호 $BCD$에 대한 원주각은 노란 활꼴의 호 위에 있는 점 $F$에 대하여 $\angle BFC$이다. 원주각은 중3 문제 해결에 열쇠가 되는 아주 중요한 성질을 가지고 있다.

유클리드 원론 3권

Proposition 20. In a circle the angle at the center is double the angle at the circumference when the angles have the same circumference as base.

원의 중심에서 만든 각(중심각)은 둘레에서 만든 각(원주각)이 같은 호를 밑변으로 가지면, 중심각 크기는 원주각 크기의 두 배가 된다.

Proposition 21. In a circle the angles in the same segment equal one another.

같은 활꼴의 원주각은 모두 같다.

요즘 교과서는 위 두 명제를 합쳐서 아래와 같이 표현한다.

같은 호에 대한 원주각의 크기는 모두 같고 중심각 크기의 1/2이다.

 

증명은 간단하지만 아주 중요하므로 잘 기억해두자. 한 호에 대한 중심각은 하나뿐이므로 원주각이 중심각의 크기의 1/2임을 보이면 끝이다. 원주각과 중심각이 이루는 위치 관계는 아래와 같이 세 가지가 있다.

1. 중심 $O$가 $\angle APB$의 한 변 위에 있는 경우

$\triangle OPA$는 $\overline{OP}=\overline{OA}$인 이등변삼각형이므로 $\angle OPA=\angle OAP$이다.

$$\angle AOB=\angle OPA +\angle OAP=2\angle OPA$$

$$\angle OPA=\frac{1}{2} \angle AOB\tag{1}$$

2. 중심 $O$가 $\angle APB$의 내부에 있는 경우

그림과 같이 지름 $PQ$를 긋는다.

(1)과 마찬가지로 $\displaystyle{\angle APQ=\frac{1}{2}\angle AOQ ,\; \angle QPB=\frac{1}{2}\angle QOB}$이다.

$$\begin{split} \angle APB&=\angle APQ+\angle QPB\\&=\frac{1}{2}\angle AOQ+\frac{1}{2}\angle QOB\\&=\frac{1}{2}\angle AOB\end{split}\tag{2}$$

3. 중심 $O$가 $\angle APB$의 외부에 있는 경우

그림과 같이 지름 $RP$를 긋자.

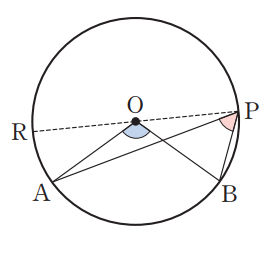
마찬가지로 위에서 증명한 바에 따라 $\displaystyle{\angle RPA=\frac{1}{2}\angle ROA,\;\angle RPB=\frac{1}{2}\angle ROB}$이다.

$$\begin{split} \angle APB&=\angle RPB-\angle RPA\\&=\frac{1}{2}\angle ROB-\frac{1}{2}\angle ROA\\&=\frac{1}{2}\angle AOB\end{split}\tag{3}$$

$\blacksquare$

문제 그림에서 $\angle x$의 크기를 구해보자.

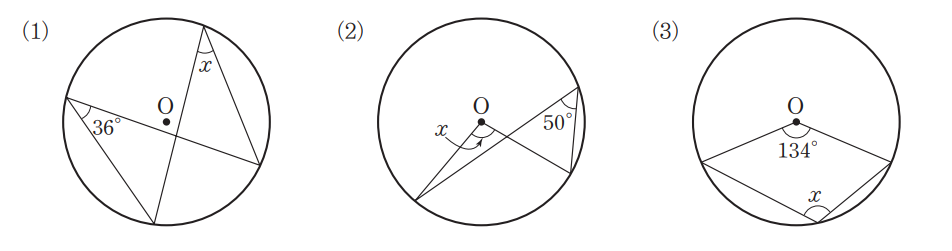
자연스럽게 반원에 대한 중심각은 $180^{\circ}$이므로 원주각은 직각임을 확인하자.

따름정리 원에 내접하는 사각형에서 한 쌍의 대각은 크기의 합이  $180^{\circ}$이다.

문제 고대 그리스 수학자 피타고라스를 따르는 학파의 상징은 정오각형의 대각선으로 이루어진 별이라고 한다. 피타고라스 학파의 상징인 별의 꼭지각의 크기를 구해보자.

현과 직선이 이루는 각

현과 직선이 이루는 각의 크기는 각의 내부에 있는 호에 대한 원주각의 크기와 같다.

위에서 증명을 제대로 이해하면 아래와 같이 세 가지 경우로 나누어서 쉽게 증명할 수 있다. 힌트 점 $A$를 지나는 지름을 보조선으로 긋는다.

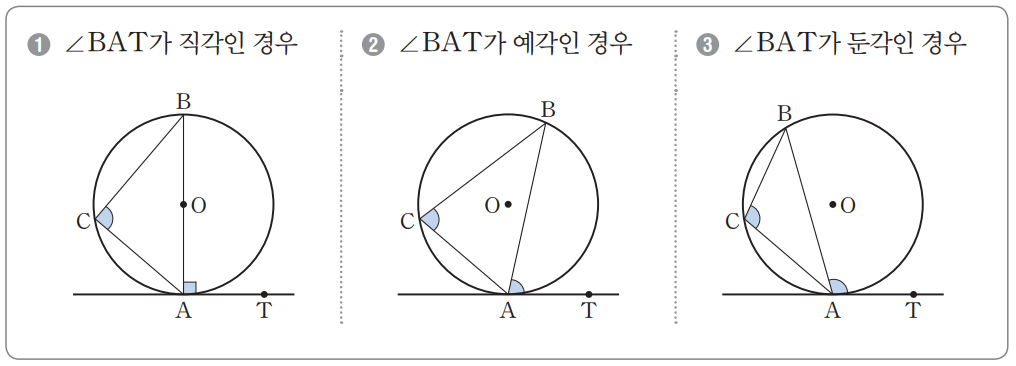
1) $\angle BAT$가 직각일 때, $\overline{AB}$는 지름이므로 반원에 대한 원주각인 $\angle BCA$는 직각이므로 성립한다.

2) $\angle BAT$가 예각일 때, 지름 $\overline{AD}$를 보조선으로 긋고 생각하면 된다.

$$\angle BCD=\angle DAB$$

$$90^{\circ}-\angle BCD=90^{\circ}-\angle DAB$$

$$\therefore \angle BCA=\angle BAT$$

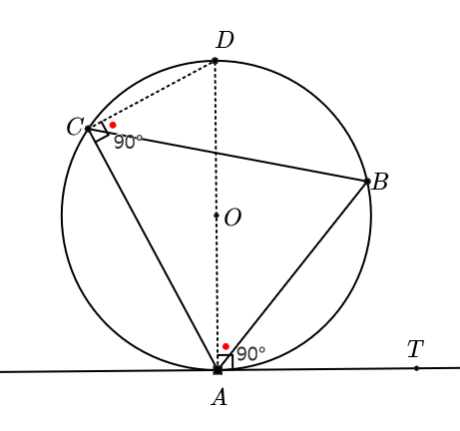
3) 2)와 마찬가지로 보이면 된다.