경우의 수_순열과 조합

"수학은 단지 경우의 수를 세는 것과 관계를 비교하는 것에 관한 것이다."

다른 사람도 아닌 수학의 왕자로 불리는 카를 프리드리히 가우스가 한 말이란다. 수학이 겨우 경우의 수를 세는 것에 불과하다는 뜻보단 경우의 수를 세는 것이 매우 중요하다는 뜻으로 받아들이자. 공통수학 1에 겨우 한 단원에 불과하지만 결코 가볍게 볼 단원은 아니다.

이 블로그에 '확률과 통계' 엄밀하게 다룬 글도 있지만 이글에선 공통수학 1 수준만 다룬다. 먼저 중학교 수학 2에 '사건과 경우의 수'가 처음 등장한다. 

사건은 같은 조건에서 반복할 수 있는 실험이나 관찰에서 나타나는 결과이다. 경우의 수는 어떤 사건이 일어나는 가짓수이다.

합의 법칙과 곱의 법칙

경우의 수를 구하는 두 가지 법칙이 있다.

두 사건 $A$, $B$가 동시에 일어나지 않을 때, 사건 $A$가 일어나는 경우의 수가 $m$, 사건 $B$가 일어나는 경우의 수가 $n$이면 사건 $A$ 또는 $B$가 일어나는 경우의 수는 $m+n$이다.

사건 $A$가 일어나는 경우의 수가 $m$이고, 그 각각에 대하여 사건 $B$가 일어나는 경우의 수가 $n$일 때,  사건 $A$, $B$가 동시에 일어나는 경우의 수는 $m\times n$이다.

메뉴판에 에스프레소 음료 8가지, 차 음료 4가지가 보인다.

1) 혼자일 때, 에스프레소 또는 차 음료를 1잔 주문하는 경우의 수는 $8+4=12$

2) 둘일 때, A는 에스프레소 1잔, B는 차 음료를 1잔을 주문하는 경우의 수는 $8\times 4=32$

※ 합의 법칙을 쓸 때, 두 사건이 동시에 일어나지 않는 사건임을 확인해야 한다.

 

더 복잡한 사건이 일어날 경우의 수를 세기 위해선 순열과 조합을 알아야 한다.

일상생활에선 조합이란 말을 주로 쓰는데 꼼꼼하게 따지면 다른 상황인데 모두 조합으로 일컫는다. 참고로 조합은 영어로 combination이고, 순열은 permutation이다.

★ 치즈-토마토-새우를 조합하여 만든 피자

★ 열쇠 번호는 2-4-7을 조합한 수

얼핏 생각하면 차이가 없지만 수학을 공부한 사람에겐 똑같이 조합으로 표현한 것이 불편하다. 피자는 토마토-치즈-새우나 치즈-새우-토마토를 조합했다고 적어도 문제가 없지만 자물쇠는 4-7-2로는 열리지 않기 때문이다. 피자는 순서를 따지지 않지만 열쇠 번호는 순서를 따져야 한다.

수학에선 이를 구분하여 피자는 조합으로 열쇠 번호는 순열로 부른다. 따라사 조합 자물쇠(combination lock)가 아니라 순열 자물쇠(permutation lock)로 불러야 한다.

중복을 허락하는 순열과 조합은 다른 글에서 다룬다. 여기서는 서로 다른 것에서 중복 없이 뽑는 것만 생각한다.

순열

16개의 당구공이 있다. 3개를 골라 일렬로 세우는 경우의 수를 구해보자.

일렬로 세우는 것에 주목해야 한다. 빈칸이 세 칸 있다고 생각하자.

첫 번째 칸을 채우는 사건이 일어날 경우의 수는 16이다. 두 번째 칸을 채우는 사건이 일어날 경우의 수는 15, 세 번째 칸을 채우는 사건이 일어날 경우의 수는 14이다. 잇달아 일어나는 사건이므로 곱의 법칙을 써야 하는 것이 자명하다. 따라서 $16\times 15\times 14$이다.

일반적으로 서로 다른 $n$개에서 $r(0<r\leq n)$개를 택하여 일렬로 나열하는 것을 $n$개에서 $r$개를 택하는 순열이라고 한다. 이 순열의 가짓수를 순열의 수라고 하고 기호로 $${}_{n}P_{r}$$로 나타낸다.

$${}_n P_{r}=\overbrace{n(n-1)(n-2)\times\cdots\times(n-r+1)}^{r\text{개}}$$

$r=n$일 때는 새로운 기호 $!$를 사용하여 나타내고 'n 계승' 또는 'n factorial'이라 읽는다.

$${}_n P_{n}=n(n-1)(n-2)\times\cdots\times3 \times 2 \times 1=n!$$

위에 있는 문제에서 남은 공 13개를 일렬로 세우는 경우의 수는 $13!$이다. 곱의 법칙에 따라 아래가 성립한다.

$${}_{16}P_3 \times 13!={}_{16}P_{16}=16!$$

이것을 일반화하여 나타내면 아래와 같다.($0<r<n$)

$${}_{n}P_r \times (n-r)!={}_{n}P_{n}=n!$$

$${}_{n}P_r =\frac{n!}{(n-r)!}\tag{1}$$

${}_n  P_0 =1,$ $0!=1$로 정하면 $r=0$, $r=n$일 때도 (1)이 성립한다.

참고: 경우에 따라 먼저 계승 함수를 정의하고 순열의 수를 정하기도 한다.

$$n!=\begin{cases} 1\,\,\,\,&( n=0)\\n\times(n-1)\times 3\times 2\times 1 \,\,&(n \not=0)\end{cases}$$

(1)은 $n$개를 일렬로 세우는 경우의 수 $n!$에서 뒤로부터 $n-r$개를 일렬로 세우는 경우의 수 $(n-r)!$을 구별하지 않고 1개로 생각하면 결국 $r$개를 일렬로 세우는 순열의 수 ${}_n P_r$와 같음을 나타낸다. 말로는 복잡하지만 이렇게 생각하는 것이 문제 해결에 도움이 될 때가 많으므로 잘 기억해 두어야 한다.

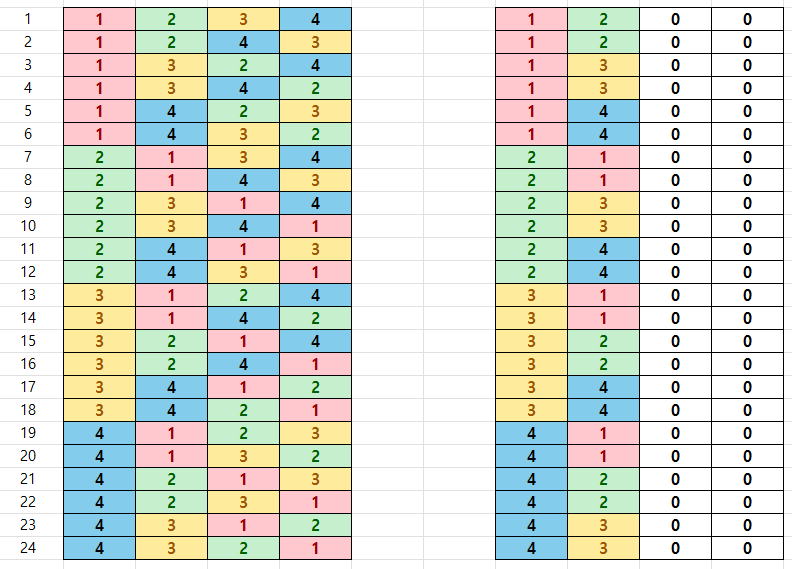
$1,\,2,\,3,\,4$로 만들 수 있는 네자리 자연수는 $4!=24$이다. 이때 십의 자리와 일의 자리를 모두 0으로 바꾸면 1234와 1243은 모두 1200이 되어 구별이 사리진다. 아래와 같이 $2!=2$로 나눈 $12$가지 된다.

$${}_4 P _2 =\frac{4!}{2!}=4\times 3 =12$$

그림 1

조합

그림 1에서 1200와 2100을 구별하지 않으면 4개에서 2개를 뽑기만 하고 일렬로 세우지 않은 것으로 생각할 수 있다. 이렇게 뽑기만 하고 뽑는 순서를 생각하지 않는 것을 조합이라고 한다.$$\frac{{}_4 P_2}{2!}=6$$이다.

일반적으로 서로 다른 $n$개에서 $r(0<r\leq n)$개를 택하는 것을 $n$개에서 $r$개를 택하는 조합이라고 한다. 이 조합의 가짓수를 조합의 수라고 하고 기호로 $${}_{n}C_{r}$$로 나타낸다.

위에서 ${}_4 C_2 \times 2!={}_4 P_2$임을 보았다.

일반적으로 나타내면 순열과 조합 사이에 아래와 같은 관계가 있다.

$${}_{n}C_r \times r!={}_{n}P_r$$

따라서 조합의 수는 아래와 같이 구한다.

$${}_{n}C_r =\frac{{}_{n} P_r}{r!}=\frac{n!}{r!(n-r)!}\tag{2}$$

순서가 없는 것에 순서를 부여할 때는 계승을 곱하고 순서가 있는 것에서 순서를 없앨 때는 계승으로 나눈다고 생각하면 된다.

예를 들어 보자.

10명에서 4명을 뽑는 것은 합격자 4명과 불합격자 6명을 정하는 것으로 보면 된다. 먼저 합격자 4명을 정한 순위가 있다고 생각하면 ${}_{10}P_4=10!/6!$이다. 여기에서 순위를 없앤다면 순열의 수를 다시 $4!$으로 나누면 된다.

$${}_{10}C_{4}=\frac{{}_{10}P_4}{4!}=\frac{10!}{6!\times 4!}$$

이처럼 순서가 있는 것으로 없는 것을 세거나 없는 것으로 순서가 있는 것을 세는 일이 자연스럽게 연결되도록 연습하자. 그래야 때에 따라 순열과 조합 가운데 알맞은 것으로 경우의 수를 쉽게 셀 수 있다.

 

https://suhak.tistory.com/2

순열(permutation)에서 조합(Combination)으로