대칭이동의 활용

대칭이동을 활용하여 문제해결을 해보자. 어떤 직선 $l$의 같은 쪽에 있는 두 점 $A,B$가 있다. 직선 위의 점 $P$에 대하여 $\overline{AP}+\overline{BP}$의 최솟값을 구하는 방법을 생각해 보자.

 

이 문제를 대수로 해결하기 위해 $A(a,b),\;B(c,d),\;P(x,0)$으로 놓고 식을 세워보자.

$\overline{AP}+\overline{BP}=\sqrt{(x-a)^2 +b^2}+\sqrt{(x-c)^2 +d^2}$이다.

$x$에 따라 정해지는 함수로 생각하면

$f(x)=\sqrt{(x-a)^2 +b^2}+\sqrt{(x-c)^2 +d^2}$

이 함수는 대수적으로 최솟값을 구하기 매우 어렵다. 이를 기하와 연관지어 생각해 보자.

대칭이동_AP BP_2.ggb

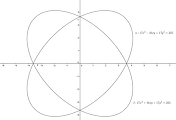
 두 선분의 길이를 더하는 것은 선분 길이를 반지름으로 하는 두 원을 이어 그려서 생각하면 된다. 그림에서 $\overline{AP}+\overline{BP}=\overline{AE_1}$인 원 $C_1$의 반지름 $\overline{AE_1}$의 변화를 생각하자. 점 $E_1$의 자취는 붉은 곡선이다.

이제 자취 위에 있는 점 가운데 점 $A$에서 가장 가까운 점을 찾으면 된다. 직선 $l$에 대한 대칭점 $H$를 생각해 보면 점 $P$가 $\overline{AH}$와 $l$의 교점일 때 최소임을 알 수 있다. ($\because \overline{AP}+\overline{PH}\geq \overline{AH}$)

 

 

대칭이동 활용2.ggb

입사각과 반사각이 같을 때 거리의 합이 최소임을 알 수 있다. 이때 경로는 바로 빛의 경로이다. 바꿔 말하면 빛은 가장 짧은 거리를 따라 이동한다. 더 정확하게 말하면 두 점 사이를 가장 짧은 시간에 도달할 수 있는 경로를 따라 이동한다고 한다. 매질이 달라지면 빛의 속도도 달라지므로 굴절이 생긴다. 물리 시간 배우는 스넬의 법칙 (snell's law) 참고 하라.