6.4 Exercises

31. An alternative derivation of the surface area formula

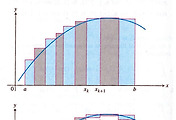
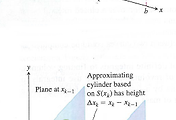
Assume $f$ is smooth on $[a,b]$ in the usual way. In the $k$th subinterval $[x_{k-1},x_{k}]$, construct the tangent line to the curve at the midpoint $m_k=(x_{k-1}+x_{k})/2$, as in the accompanying figure.

 

$$r_1+r_2=2f(m_k)$$

If line $l$ is the tangent Line at point $(m_k, f(m_k))$, then

$$l:y-f(m_k)=f^{\prime }(m_k)(x-m_k)$$

$(x_{k-1},r_1 ), (x_k, r_2)$ are put on $l$

$$r_1-f(m_k)=f^{\prime }(m_k)(x_{k-1}-m_k)-------(1)$$

$$r_2-f(m_k)=f^{\prime }(m_k)(x_k-m_k)----------(2)$$

$(1)-(2)$

$$r_1-r_2=f^{\prime }(m_k)(x_{k-1}-x_k)=f^{\prime }(m_k)\mathrm{\Delta }{x}_k$$

$$\therefore r_1=f(m_k)-f^{\prime }(m_k)\frac{\mathrm{\Delta }{x}_k}{2},r_2=f(m_k)+f^{\prime }(m_k)\frac{\mathrm{\Delta }{x}_k}{2}$$

The lateral surface area of the cone swept out by the tangent line segment as it revolves about the x-axis is

$$S_k=2\pi f(m_k)\sqrt{(\mathrm{\Delta }{x}_k{)}^2+(\mathrm{\Delta }{y}_k{)}^2}=2\pi f(m_k)\sqrt{1+(f^{\prime }(m_k){)}^2}\mathrm{\Delta }{x}_k$$

$$S\approx \sum _{k=1}^n{S}_k=\sum _{k=1}^{n}2\pi f(m_k)\sqrt{1+(f^{\prime }(m_k){)}^2}\mathrm{\Delta }{x}_k$$

$$\therefore S=\underset{n\to \mathrm{\infty }}{lim}\sum _{k=1}^{n}2\pi f(m_k)\sqrt{1+(f^{\prime }(m_k){)}^2}\mathrm{\Delta }{x}_k={\int }_a^{b}2\pi f(x)\sqrt{1+(f^{\prime }(x){)}^2}dx$$