피타고라스 정리
수학이야기/기하벡터 2010. 2. 11. 09:52피타고라스 정리는 수학을 조금이라도 공부한 이라면 누구나 알고 있는 가장 널리 알려진 정리이다. 널리 알려진만큼 증명도 여러가지인데 증명이 아주 많다는 것은 뜻밖에 많이 알려지지 않았다.
증명#1
가장 널리 알려진 증명은 유클리드의 두 증명이다. 아래 그림은 여러가지 이름으로 불리우는데 '신부의 의자(Bride's Chair)'가 가장 인기있는 이름이다.
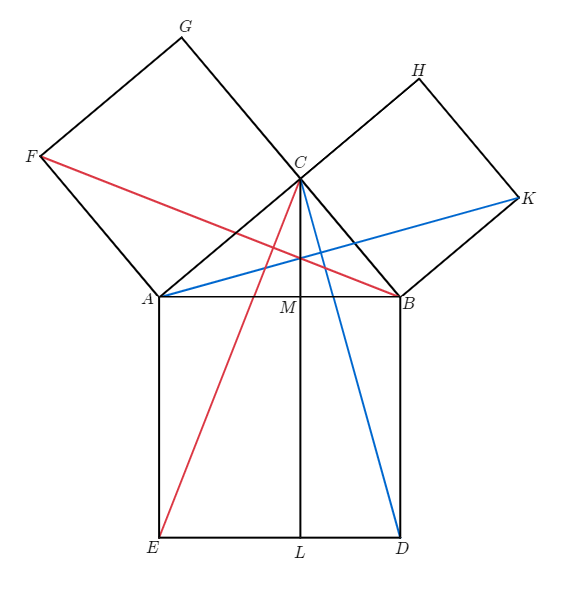
$\Delta ABF$와 $\Delta AEC$ 에서
$$AE=AB, AF=AC$$
$$\angle BAF= \angle BAC +\angle CAF =\angle CAB + \angle BAE =\angle CAE$$
$$\therefore\quad \Delta ABF\equiv \Delta AEC$$
$\Delta ABF$는 밑변이 $AF$이고 높이가 $AC$이므로 정사각형 $ACGF$ 넓이의 반이다.
$$2\Delta ABF=AC^2$$
$C$에서 $AE$에 평행인 선을 긋고 $AB, EL$과 만나는 점을 $M, L$이라고 하자.
$\Delta AEC$는 밑변이 $AE$ 높이가 $AM$이므로 사각형 $AELM$ 넓이의 반이다.
마찬가지로,
$$AB=BD, BC=BK$$
$$\angle ABK= \angle ABC +\angle CBK =\angle ABC+ \angle ABD=\angle CBD$$
$$\therefore \Delta ABK \equiv \Delta BCD$$
$$2\Delta ABK =BC^2$$
$2\Delta BCD=$ 사각형 $BDLM$
$$\therefore AC^2 +BC^2 =AB^2$$
이제 아래 그림을 보자. 그림과 같이 두 직각삼각형을 돌려주면 증명 끝.


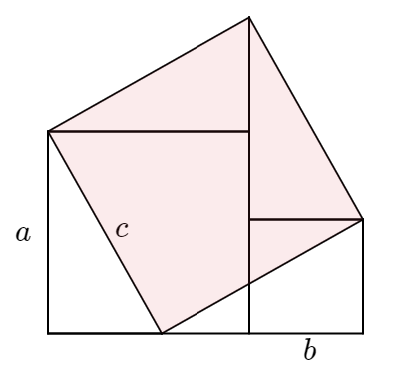


아래 그림에서 각각의 직각 삼각형 넓이를 모두 더하면 $$\displaystyle{\frac{1}{2} ab \times 4 =2ab}$$이고 가운데 정사각형 넓이는 $(b-a)^2$이므로 $$c^2 =(b-a)^2 + 2ab=a^2 +b^2$$증명 끝.