포드 원(Ford circles)

아폴로니안 가스켓을 공부하다가 포드-원(Ford circles)도 공부하게 되었다. 이런 재밌는 기하를 왜 이제야 알았을까? 포드-원은 아래와 같이 평행한 두 직선 사이에 접하는 원을 한 없이 그려서 만드는 도형이다. 아폴로니안 가스켓$(-1,2,2,3)$을 반전시켜서 얻어지는 도형에서 $x$축에 접하는 원만 따로 모으면 된다.

처음 시작하는 두 원의 반지름이 $1$이라고 하면 이어지는 원들의 중심은 $(p/q,1/2q^2)$인데 $x$좌표만 놓고 보면 아주 재밌는 수열(Farey sequence)을 이룬다. 

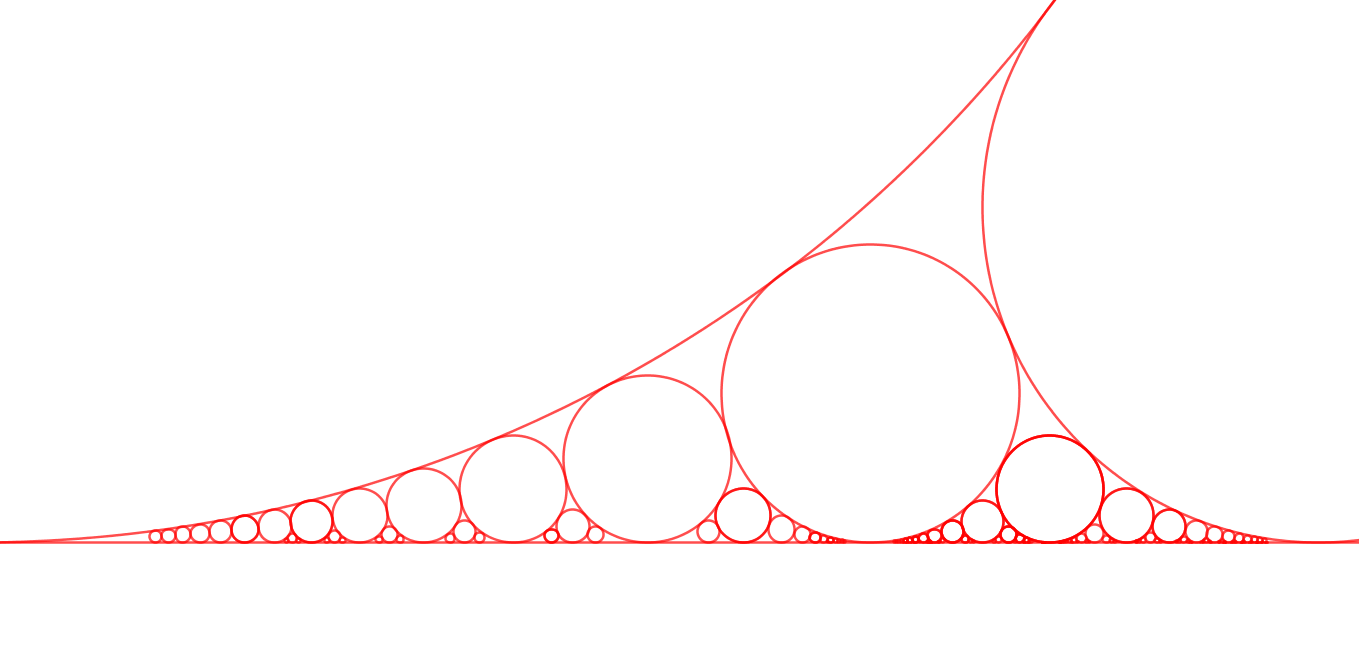
이제 새로운 연산을 정의하자. 

$$\frac{p}{q}\oplus \frac{r}{s}=\frac{p+r}{q+s}$$

마치 분수 덧셈을 모르는 아이들 계산처럼 보인다. 이 연산으로 얻어지는 값을 가운데 적어나가는 수열이 파레이 수열(farey sequence)이다. 파스칼의 삼각형을 생각하면 쉽게 이해할 수 있다. 이 수열에 있는 수들이 포드-원 중심의 $x$좌표가 된다. 이때, 중심 $x$좌표의 분모가 같으면 반지름도 같다. 원들의 중심이 $(p/q,1/2q^2)$이면 원이 $x$축에 접하므로 반지름은 당연히 $1/2q^2$이다.

이웃하는 세 원의 반지름을 왼쪽 $r_{L}$, 중간 $r_{M}$, 오른쪽 $r_{R}$이라고 하면 아래를 만족시킨다.

$$\begin{equation}\frac{1}{\sqrt{r_{M}}}=\frac{1}{\sqrt{r_{L}}}+\frac{1}{\sqrt{r_{R}}}\end{equation}$$

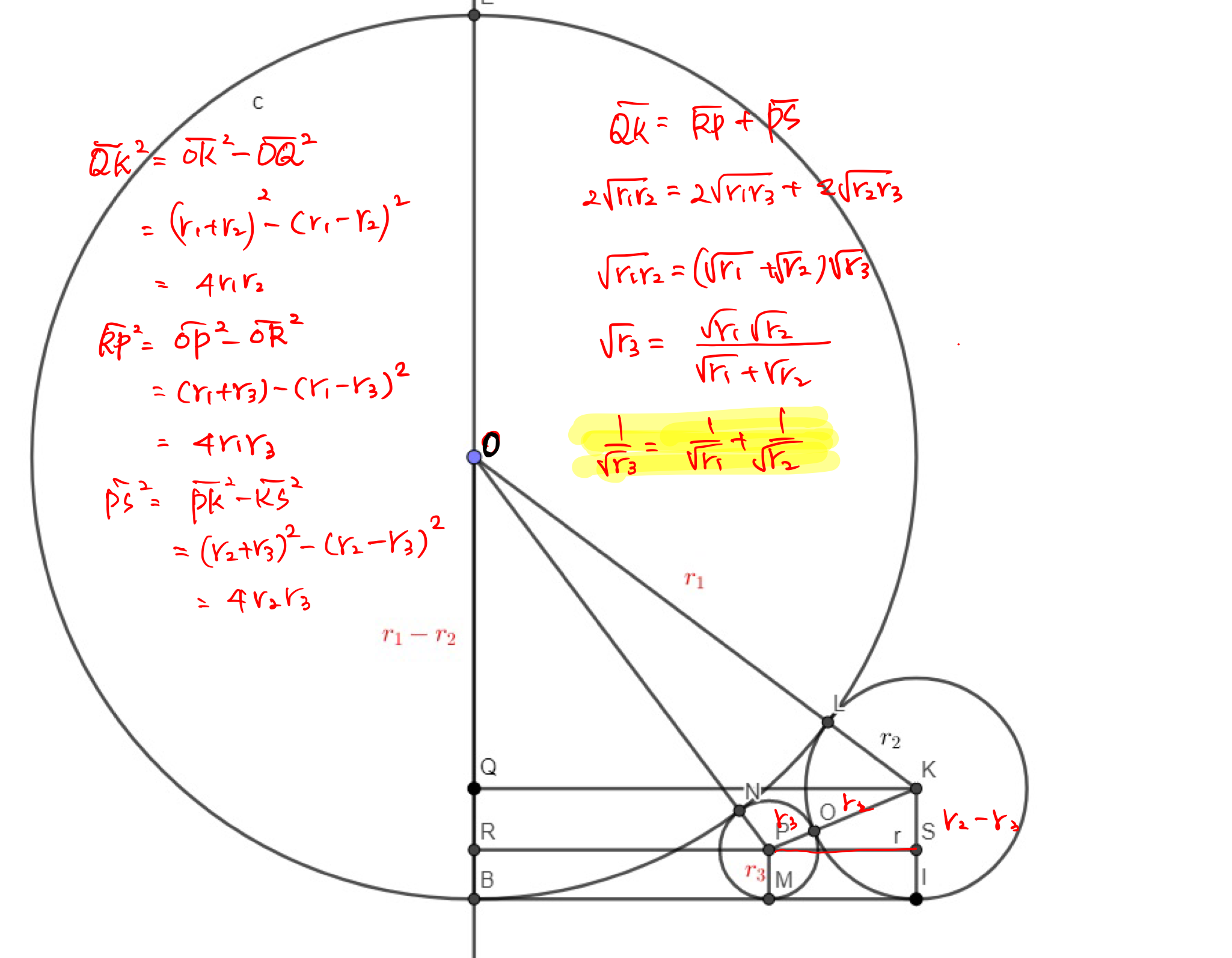
여기서 반지름의 역수를 곡률로 정의하고 식을 정리해 보자.

$$\kappa_1=\frac{1}{r_{L}}, \kappa_2=\frac{1}{r_{R}}, \kappa_3=\frac{1}{r_{M}}$$

$$\sqrt{\kappa_3}=\sqrt{\kappa_1}+\sqrt{\kappa_2}$$

$$\kappa_3=\kappa_1+\kappa_2+2\sqrt{\kappa_1}\sqrt{\kappa_2}$$

$$(\kappa_3-\kappa_1-\kappa_2)^2=(2\sqrt{\kappa_1}\sqrt{\kappa_2})^2$$

$${\kappa_3}^2+{\kappa_1}^2+{\kappa_2}^2=2({\kappa_1}{\kappa_2}+{\kappa_2}{\kappa_3}+{\kappa_3}{\kappa_1})$$

직선을 반지름이 무한대인 원으로 생각하면 곡률은 $0$이다. 이 식을 일반화하면 아래와 같은 데카르트 정리를 얻는다.

$${\kappa_1}^2+{\kappa_2}^2 +{\kappa_3}^2+ {\kappa_4}^2=2({\kappa_1}{\kappa_2}+{\kappa_2}{\kappa_3}+{\kappa_3}{\kappa_4}+{\kappa_4}{\kappa_1})$$

이 정리는 아래와 같은 꼴로 정리할 수 있다.

$$2({\kappa_1}^2+{\kappa_2}^2 +{\kappa_3}^2+ {\kappa_4}^2)=({\kappa_1}+{\kappa_2}+{\kappa_3}+{\kappa_4})^2$$