아르키메데스와 포물선

아래와 같이 아르키메데스(?. 287 – ?. 212 BC)는 구적법으로 포물선과 직선으로 둘러싸인 부분의 넓이를 구했다. 아르키메데스 소진법으로 부르는 방법을 보면 왜 그의 이름이 수쳔 년간 기억되는가 알게 된다. 기원전에 어찌 이런 생각을 했을까 정말 놀랍다.

 

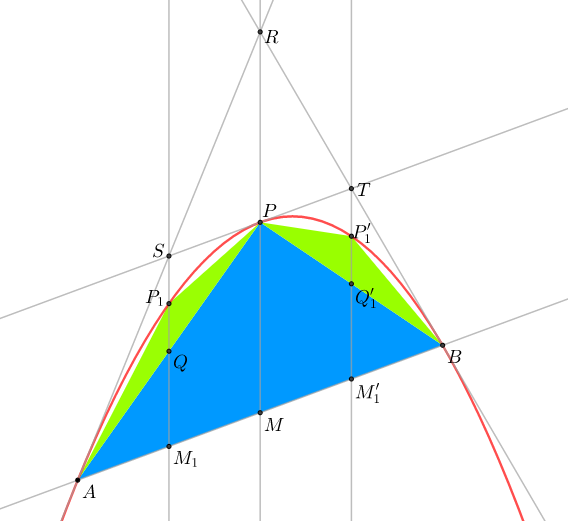
정의 포물선 단면(parabolic segment) 그림과 같이 포물선을 자르는 선분 $AB$와 잘린 포물선으로 둘러싸인 도형이다. 이때 선분 $AB$ 가장 멀리 떨어진 점 $P$를 꼭짓점(Vertex)이라 한다.

멋진 풀이를 맛보려면 먼저 포물선이 가지고 있는 성질을 몇 가지 정리해야 한다. 

포물선 위에 있는 점은 준선과 초점에 이르는 거리가 같다. 

정리 1. 준선 위에 있는 점과 초점을 수직이등분하는 선은 포물선에 접한다.

정리 2. 그림에서 $4p \overline{VT}=\overline{PT}^2$이다.

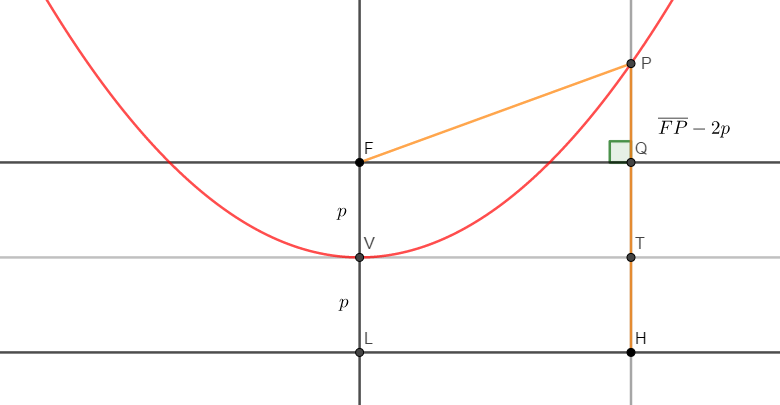
증명 먼저 초점 $F$에서 준선에 내린 수선의 발은 $L$, 꼭짓점은 $V$이라고 하자.

$\overline{FV}=\overline{VL}=p$라고 하자.

$\overline{FL}<\overline{PH}$일 때를 보이자.

$$\begin{split} \overline{FP}^2 &= \overline{FQ}^2 +\overline{PQ}^2 \\ \overline{FP}^2 & = \overline{VT}^2 +(\overline{PH}-2p)^2 \\ \overline{FP}^2 & = \overline{VT}^2 +(\overline{FP}-2p)^2 \\ \overline{FP}^2 & = \overline{VT}^2 + \overline{FP}^2 - 4 p \overline{FP}+4p^2 \\ 4p(\overline{FP}-p)& = \overline{VT}^2 \\ 4p(\overline{PH}-p)& = \overline{VT}^2 \\ 4p \overline{PT}& = \overline{VT}^2 \end{split}$$

$\overline{FL}<\overline{PH}$일 때도 마찬가지다.

$\blacksquare$

데카르트 좌표로 쓰면 $y^2 =4px$ 또는 $x^2 =4py$와 같다.

정리 3. 포물선의 꼭짓점 $V$를 지나고 준선에 수직인 직선 $l$이 있다. 직선 $l$ 위에 그림과 같이 $\overline{AV}=\overline{BV}$인 두 점 $A, B$를 잡고 $B$를 지나고 $l$에 수직인 직선이 포물선과 만나는 점을 $P$라 하면 직선 $AP$는 포물선의 접선이다.

귀류법으로 증명해 보자.

직선 $AP$가 접선이 아니라 포물선을 $K$에서 자른다고 하자. 점 $F$를 지나고 직선 $Ab$에 수직인 직선이 포물선과 $G$에서 만난다고 하자.

$$\frac{\overline{GD}^2}{\overline{PB}^2}>\frac{\overline{FD}^2}{\overline{PB}^2}=\frac{\overline{AD}^2}{\overline{AB}^2}\tag{1}$$

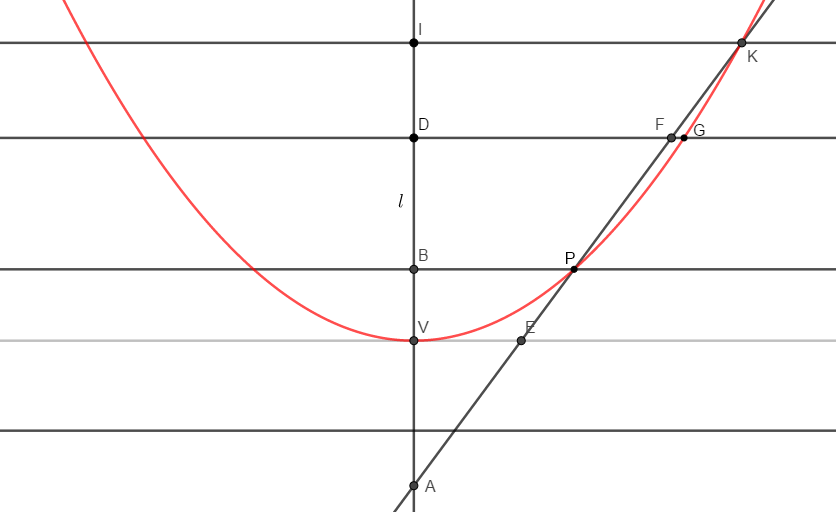
두 점 $P$와 $G$는 포물선 위에 있는 점이므로 아래가 성립한다.

$$\overline{GD}^2 =k\overline{VD},\quad \overline{PB}^2=k\overline{VB}$$

따라서, $$\frac{\overline{GD}^2}{\overline{PB}^2}=\frac{\overline{VD}}{\overline{VB}}$$이다. 그러므로

$$\frac{\overline{VD}}{\overline{VB}}>\frac{\overline{AD}^2}{\overline{AB}^2}\Rightarrow \frac{4\overline{VD}\cdot \overline{VA}}{4\overline{VB} \cdot \overline{VA}}> \frac{\overline{AD}^2}{\overline{AB}^2}$$

$$\frac{4\overline{VD}\cdot \overline{VA}}{\overline{AD}^2}>\frac{4\overline{VB} \cdot \overline{VA}}{\overline{AB}^2}=1$$

이다. 주어진 조건에서 $\overline{VA}=\overline{VB}$이므로 $\overline{AB}^2 =4 \overline{VB}\cdot \overline{VA}$이고 $\overline{VD}>\overline{VA}$이므로 $4\overline{VD}\cdot \overline{VA}>\overline{AD}^2$이다.

$\overline{AD}=\overline{VA}+\overline{VD}$이므로 $$4\overline{VD}\cdot \overline{VA}>(\overline{VA}+\overline{VD})^2$$이다. 정리하면 $0> (\overline{VA}-\overline{VD})^2$이므로 모순이다.

$\blacksquare$

정리 4 포물선 위의 두 점 $A,B$를 지나는 접선이 만나는 점은 선분 $AB$의 중점 $M$을 지나고 준선에 수직인 직선 위에 있다.

증명 두 접선이 만나는 점을 $C$라고 하자.

그림에서 접선은 선분 $DF$과 선분 $EF$의 수직이등분선이다.

$$\overline{CD}=\overline{CF}=\overline{CE}$$

$\triangle CDE$는 이등변 삼각형이므로 중선은 $M$을 지난다.

$\blacksquare$

따름 정리 점 $V$를 지나는 접선과 직선 $AB$는 평행이다.

증명 점 $V$를 지나는 접선이 두 접선 $AC$와 $BC$와 만나는 점 $D,E$라고 하자.

두 점 $D,E$를 지나고 직선 $CM$과 평행한 직선은 각각 두 선분 $AM$과 $BM$의 중점 $G,J$를 지난다.

$$\overline{AO}=2\overline{HD}=\overline{VC},\quad \overline{BP}=2\overline{JE}=\overline{VC}$$

$$\overline{AO}=\overline{BP}, \quad \overline{AO}//\overline{BP}$$

사각형 $ABPO$는 평행사변형이므로 $V$를 지나는 접선과 직선 $AB$는 평행하다.

따라서 $V$는 포물선 단면 $ABV$의 꼭짓점이다.

두 점 $I,L$도 꼭짓점이다.

 

정리 5 선분 $PB$가 포물선을 자를 때, 점 $Z$는 선분 $PB$의 중점이라 하자. 직선 $ZV$와 $AB$가 평행이 되도록 $V$에서의 접선 위에 점 $B$를 잡는다. 선분 $VA$ 위에 점 $C$를 잡고 직선 $CD$가 직선 $ZV$와 평행이 되도록 점 $D$를 잡으면

$$\frac{\overline{CD}}{\overline{AB}}=\frac{\overline{VC}^2}{\overline{VA}^2}$$

이다.

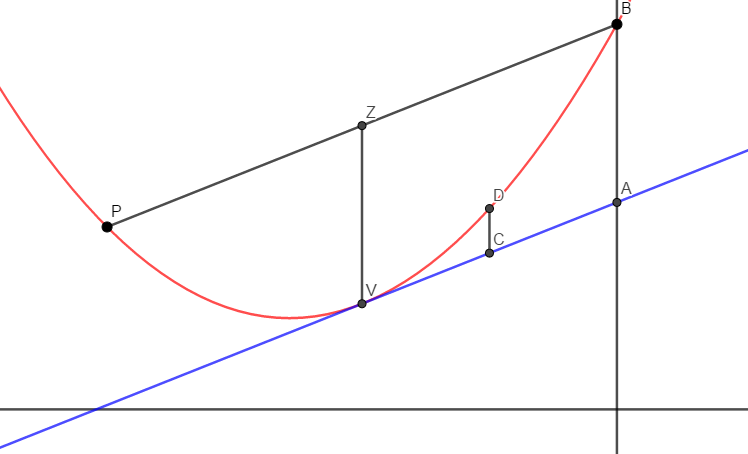
직선 $PB$가 준선과 평행하다면 명백하다.

직선 $PB$가 준선과 평행하지 않을 때를 보이자.

아래와 그림과 같이 점 $V$에서 초점과 꼭짓점을 지나는 직선(대칭축)에 수선의 발 $E$를 잡는다.

점 $E,G$를 지나고 준선에 평행인 직선을 긋고 나머지 점 $V, V_1,I, I_1, J, J_1$를 잡는다.

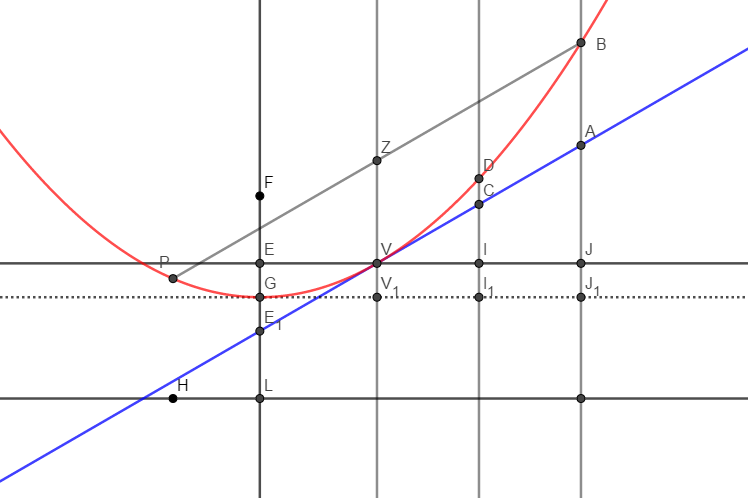
직선 $VA$가 접선이므로 정리 3에 따라 $\overline{EG}=\overline{GE_1}$이다. 길이를 $y_1$이라고 하자.

$$\overline{VV_1}=\overline{II_1}=\overline{JJ_1}=y_1$$

$\overline{GV_1}=x_1,\overline{GI_1}=x_2,\overline{GJ_1}=x_3$이라고 하면 $\overline{EV}=x_1,\overline{EI}=x_2,\overline{EJ}=x_3$이다.

정리 2에 따라 

$$x_1^2 =k \overline{VV_1}=ky_1,x_2^2 =k\overline{DI_1}, x_3^2=k\overline{BJ_1}$$

$\triangle VEE_1 \sim \triangle VIC \sim \triangle VJA$이므로

$$\frac{\overline{EE_1}}{\overline{EV}}=\frac{\overline{IC}}{\overline{VI}}=\frac{\overline{JA}}{\overline{VJ}}=\frac{2y_1}{x_1}=\frac{2x_1^2 /k}{x_1}=\frac{2x_1}{k}$$

정리하면 

$$k\overline{IC}=2x_1\overline{VI}=2x_1 (x_2 -x_1),\quad k\overline{JA}=2x_1\overline{VF}=2x_1 (x_3 -x_1)\tag{2}$$

$$\frac{\overline{CD}}{\overline{AB}}=\frac{\overline{DI_1}-\overline{CI}-\overline{II_1}}{\overline{BJ_1}-\overline{AJ}-\overline{JJ_1}}=\frac{x_2^2/k -x_1^2/k-\overline{CI}}{x_3^2/k -x_1^2/k-\overline{AJ}}=\frac{x_2^2 -x_1^2-k\overline{CI}}{x_3^2 -x_1^2-k\overline{AJ}}$$

(2)를 대입하면

$$\frac{\overline{CD}}{\overline{AB}}=\frac{x_2^2 -x_1^2-2x_1 (x_2 -x_1)}{x_3^2 -x_1^2-2x_1 (x_3 -x_1)}=\frac{(x_2 -x_1)^2}{(x_3 -x_1)^2}=\frac{\overline{VI}^2}{\overline{VJ}^2} $$

$\triangle VIC \sim \triangle VJA$이므로

$$\frac{\overline{VI}^2}{\overline{VJ}^2} =\frac{\overline{VC}^2}{\overline{VA}^2} $$

$$\frac{\overline{CD}}{\overline{AB}}=\frac{\overline{VC}^2}{\overline{VA}^2}$$

$\blacksquare$

아르키메데스는 소진법(exhaustion)으로 부르는 구적법으로 포물선 단면은 녹색 삼각형 넓이의 $4/3$배가 된다는 정리를 찾았다. 먼저 간단하게 정리해 두고 다음 글에서 자세하게 정리한다.

아르키메데스는 그림과 같이 포물선 단면의 꼭짓점과 현을 잇는 삼각형을 계속해서 지워나가면 된다고 생각했다.

처음에 있는 삼각형 넓이를 $a_0$라고 하자.

첫 단계에서 만들어지는 파란 삼각형과 녹색 삼각형의 중선 길이 사이 비는 $1:4$이다.

중선을 밑변으로 하는 삼각형을 생각하면 높이는 비가 $1:2$이므로 따라서 넓이는 비가 $1:8$이다.

$n$ 만들어 지는 삼각형 개수는 $2^{n}$개이다.

무한급수로 나타내면 아래와 같다.

$$A=a_0 +2\cdot \frac{1}{8}a_0 + 2^2 \cdot \frac{1}{8^2}a_0 +\cdots = \sum_{n=0}^{\infty} a_0 \left( \frac{1}{4} \right)^{n} = \frac{a_0}{1-1/4}=\frac{4}{3} a_0$$