칼라일 원(Carlyle Circle)
수학이야기/기하벡터 2020. 8. 6. 19:00위키백과 칼라일 원을 우리말로 옮긴다.
칼라일 원은 좌표평면에 있는 이차방정식과 관계된 원이다. 이 원이 $x$축과 만나는 점은 주어진 이차방정식의 해이다. 칼라일 원은 정다각형의 작도법을 발전시키는 데 사용되었다.
정의
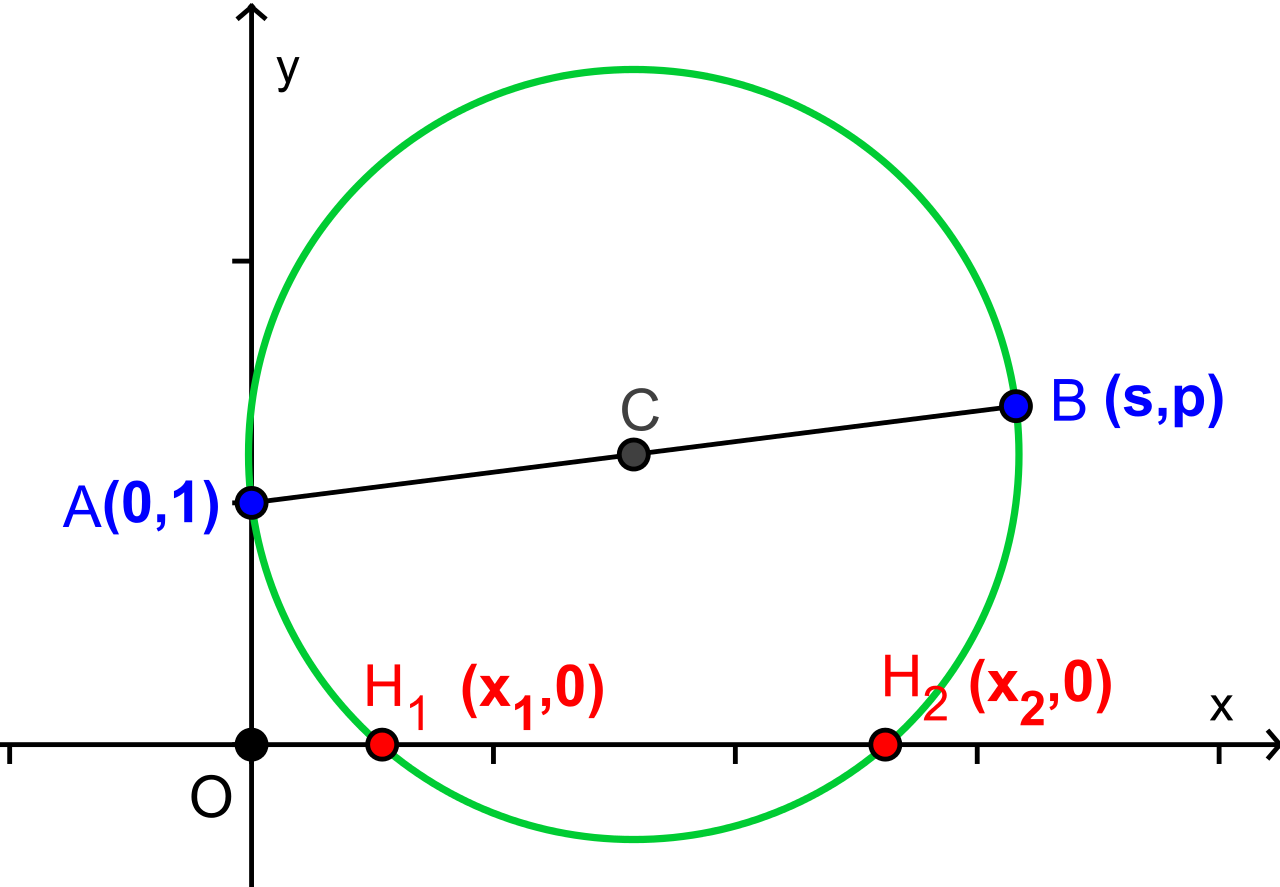
아래와 같이 주어진 이차방정식의 '칼라일 원'은 두 점 $A(0,1)$과 $B(s,p)$를 지름의 양 끝으로 가지는 원이다.
$$x^2 -sx+p=0$$
정의 확인
선분 $AB$가 지름인 원의 방정식은
$$x(x-s)+(y-1)(y-p)=0$$
이고 이 원과 $y=0$과 만나는 점인$x$ 절편은 주어진 이차방정식의 근이다.
$$x^2 -sx+p=0$$
정다각형 작도하기
정오각형을 작도하는 문제는 아래 방정식의 근을 구하는 문제와 같다.
$$z^5 -1=0$$
한 근인 $z_0=1$는 $P_0(1,0)$과 관계있다. 이제 $z-1$을 소거한 방정식에서 나머지 근을 찾으면 된다.
$$z^4 +z^3 +z^2 +z+1=0$$
$\displaystyle{\omega=exp(2\pi i/5)=\cos \frac{2\pi}{5}+i\sin\frac{2\pi}{5}}$라고 한다면 네 근은 $\omega,\omega^2,\omega^3,\omega^4$으로 나타낼 수 있다. 네 근과 관계된 점을 각각 $P_1,P_2,P_3,P_4$라고 하자.
$$p_1=\omega+\omega^4,\quad p_2=\omega^2 +\omega^3$$
로 놓으면 근과 계수와의 관계에 따라서
$$p_1+p_2=\omega+\omega^4+\omega^2+\omega^3=-1$$
이다. 그리고
$$p_1p_2=(\omega+\omega^4)(\omega^2+\omega^3)=\omega^3+\omega^4+\omega^6+\omega^7=\omega^3+\omega^4+\omega+\omega^2=-1$$
이다. 드모르간 공식 $(\cos \theta+i\sin \theta)^n=\cos n \theta+i\sin n \theta$을 쓰면 $\omega^6=\omega,\;\;\omega^7=\omega^2$임을 쉽게 보일 수 있다.
$p_1,p_2$를 근으로 가지는 이차방정식은
$$x^2 +x-1=0$$이다. 이 방정식의 칼라일 원은 두 점 $(0,1),(-1,-1)$을 지름의 양 끝점으로 하는 원이다. 중심은 $(-1/2,0)$이다.
$$p_1=2\cos\frac{2\pi}{5},\quad p_2=2\cos \frac{4\pi}{5}$$
이므로 $p_1,p_2$와 관계된 칼라일 원을 작도하면 $P_1,P_2,P_3,P_4$을 찾을 수 있다.
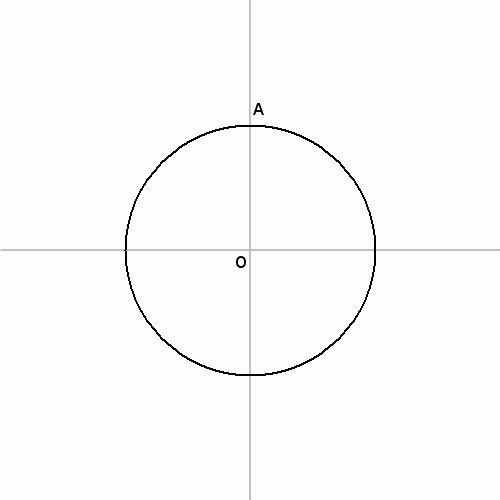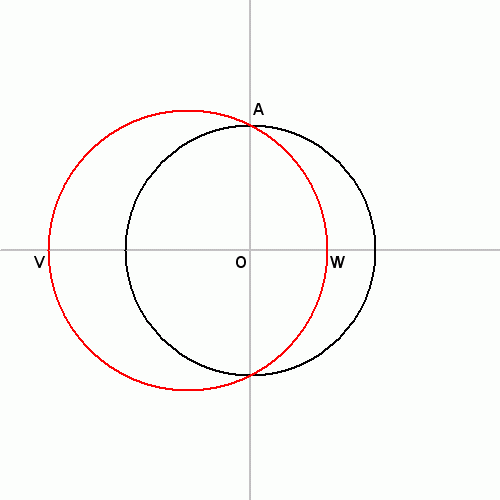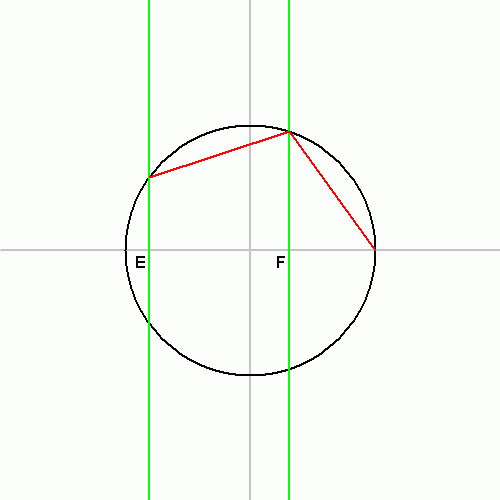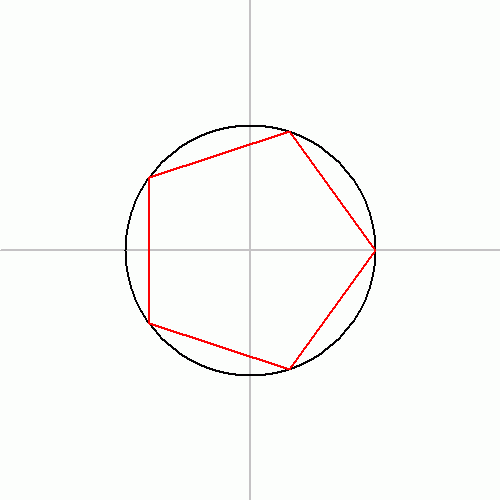
- 정오각형을 내접시킬 중심이 $O$인 원을 그린다.
- 중심을 지나는 직선 $l$이 원과 만나는 왼쪽에 있는 점을 $B$라고 하자
- 중심을 지나고 $l$에 수직인 직선이 원과 만나는 한 점을 $A$라고 하자.
- $O$와 $B$의 중점 $M$을 작도한다.
- $M$을 중심으로 $A$를 지나는 원을 그려서 $l$과의 교점 가운데 원 안에 있는 점을 $W$, 바깥에 있는 점을 $V$로 놓는다.
- 선분 $OW$의 수직 이등분선과 원 $C$의 교점이 정오각형 꼭짓점이다.
- 선분 $VO$의 수직이등분선과 원 $C$의 교점이 정오각형 꼭짓점이다.
- 다섯 번째 꼭짓점은 B이다.
가우스는 19살이던 1796년에 정다각형을 작도하는 일은 삼각함수 값을 사칙연산과 제곱근으로 나타내는 일과 동치임을 보이는 방법으로 정17각형을 작도할 수 있음을 보였다고 한다.
$$\begin{align} 16\,\cos\frac{2\pi}{17} = & -1+\sqrt{17}+\sqrt{34-2\sqrt{17}}+ 2\sqrt{17+3\sqrt{17}- \sqrt{34-2\sqrt{17}}- 2\sqrt{34+2\sqrt{17}}}\\ = & -1+\sqrt{17}+\sqrt{34-2\sqrt{17}}+ 2\sqrt{17+3\sqrt{17}- \sqrt{170+38\sqrt{17}}}. \end{align}$$
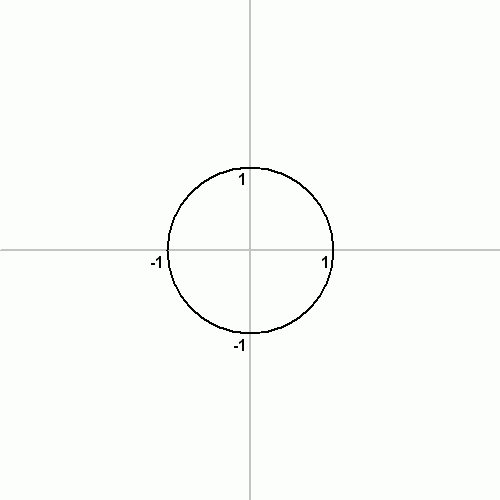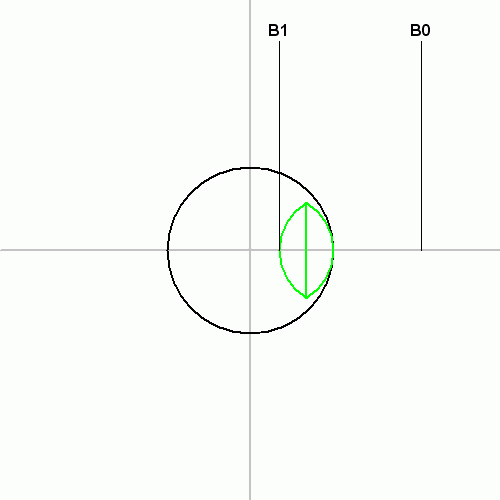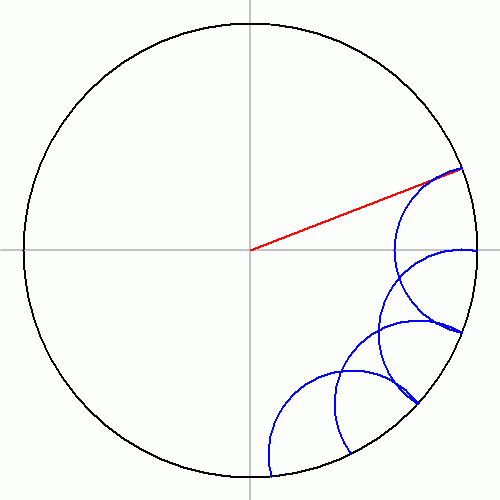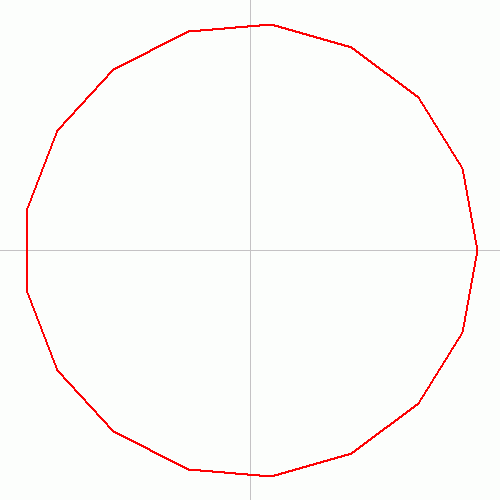
하지만 실제로 작도법은 한참이 지나서야 만들어졌다. 1893년 리치몬드(Herbert William Richmond) 아래에 있는 작도법을 보였다. 아래 그림에서 붉은 원들이 칼라일 원이다. 정오각형보다는 복잡해서 하나가 아니라 넷이 필요하다.
정257각형
칼라일 원 24개를 써서 정257각형을 작도할 수 있다. 이들 가운데 하나와 관계된 이차방정식은 $x^2 +x-64=0$이다.

정65537각형은 $x^2 +x-2^{14}=0$과 관련 있다. 이것은 그림으로 보여줘도 원이나 다를 바 없을 것이다.
역사
하워드 이브 (1911- 2004)에 따르면 수학자 존 레슬리(1766-1832)는 그의 책 <기하학의 근본: Elements of Geometry>에서 원으로 이차방정식의 근을 기하적인 작도로 표현하였고 이 생각은 제자인 토마스 칼라일(1795–1881)이 제공하였다고 적었다. 그러나 레슬리 책에는 비슷한 원 작도가 포함되어 있으나 직교 좌표계나 2차 함수와 근을 쓰지 않고 기초 기하학적 용어로만 쓰여 있다.
직선을 내분하거나 외분할 때 선분 아래에 있는 사각형이 주어진 사각형과 같아야 한다.
— John Leslie, 기하학 요소 , prop. XVII, p. 176 (복사본 (구글))
1867년 오스트리아의 엔지니어인 릴(Eduard Lill)은 다항식의 근을 그래픽으로 결정하는 방법을 발표했다.(릴 방법). 이차 함수에 적용하면, 칼라일 해와 레슬리(Leslie) 문제(그림 참조)를 해결하는 칼라일 원의 지름을 포함하고 있는 사다리꼴 그림을 얻을 수 있다. 1925년 GA Miller의 기사에서 정규 2차 함수에 적용된 Lill의 방법을 조금 고치면 주어진 함수의 근을 기하학적으로 작도하고 훗날 '칼라일 원'으로 부르는 원을 현대적 정의로 설명할 수 있음을 밝혔다.
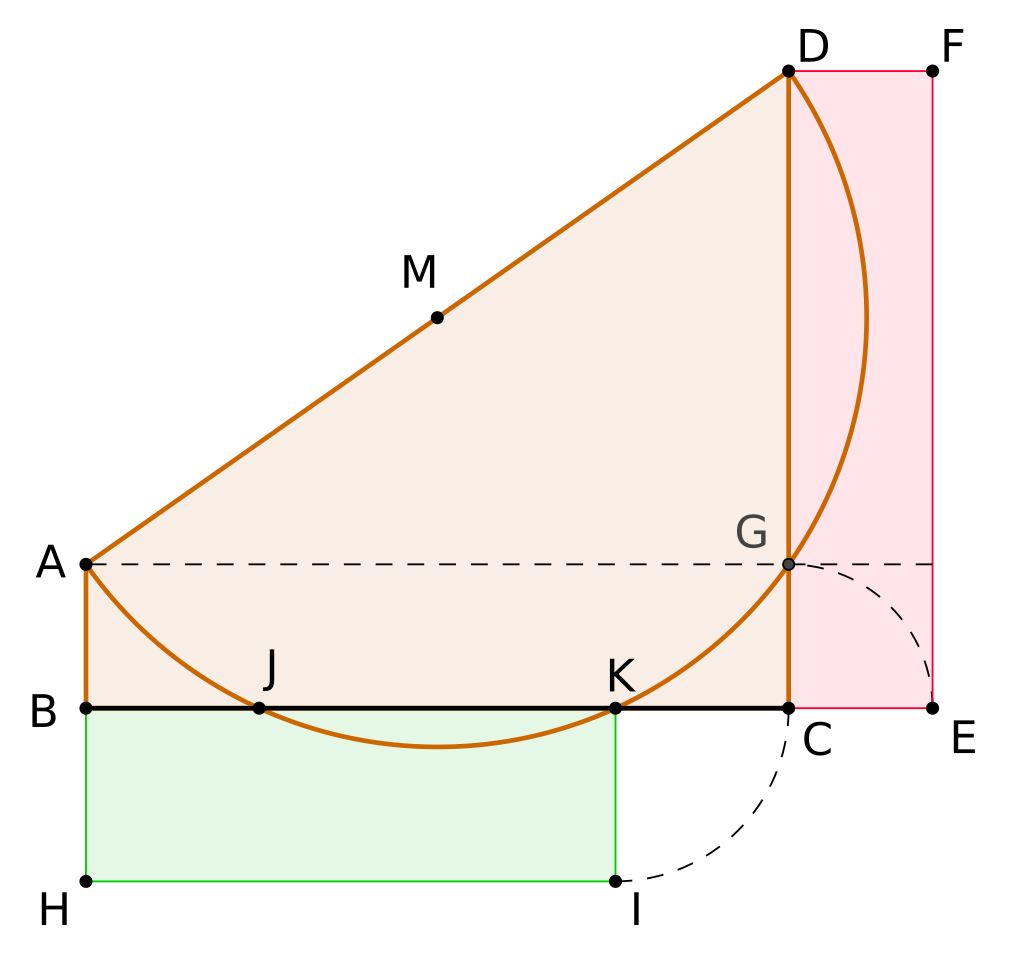
이브는 <수학사 소개 (1953)>에서 연습 문제 하나로 현대적인 의미로 원을 사용했고 레슬리와 칼라일과의 관련성을 적었다. 이후 출판물은 '칼라일 원, 칼라일 방법 ' 또는 '칼라일 알고리즘 '으로 부르고 있지만 독일에서는 '릴 원Lill circle(Lill-Kreis)'라고 쓰기도 한다.드 템플(DeTemple)이 1989년과 1991년 정다각형을 작도하는 도구로 칼라일 원을 사용하여 오각형, 17각형 , 257-gon , 65537-gon을 작도하였다. 라디슬라브 베란(Ladislav Beran)은 1999 년에 정규 2차 함수의 복소수 근을 작도하는데 칼라일 원을 사용하는 방법을 설명했다.







