피타고라스 나무

프랙탈 도형인 피타고라스 나무가 있다. 만드는 일은 아주 단순하다.

정사각형 하나를 그린다.

빗변이 되는 한 변을 고르고 적당한 각으로 직각삼각형을 그린다.(꼭 직각삼각형이 아니라도 나무는 그려진다.)

나머지 두 변에 정사각형을 그린다. 같은 일을 되풀이 한다.

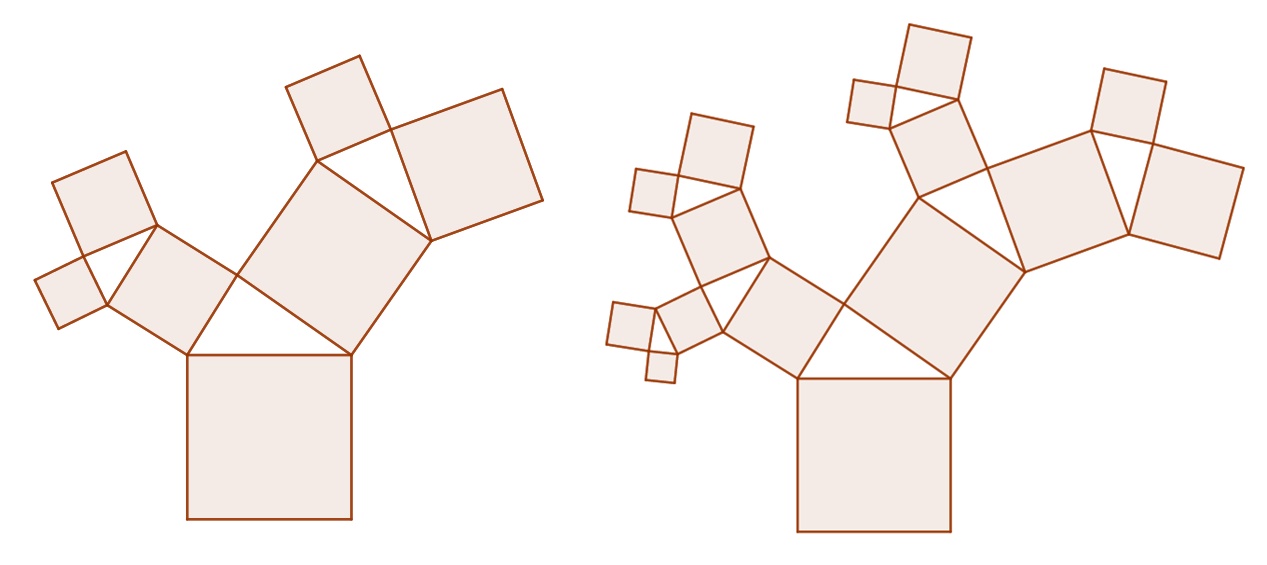
아래 연결고리를 눌러서 움직이는 그림으로 보자.

움직이는 그림으로 보기

아래 그림과 같이 한 변의 길이가 $1$인 정사각형의 한 꼭짓점을 원점으로 삼각형의 한 각을 $\alpha$라 하자. 정사각형의 점을 $\mathbf{x}$라고 하면 아래와 같은 함수로 새로 그리는 정사각형의 점을 구할 수 있다.

왼쪽에 있는 정사각형의 점은 원점을 중심으로 시계반대방향으로 $\alpha$ 회전변환하고 닮음비가 $\cos \alpha$인 닮음변환한 다음 $y$축 방향으로 $1$만큼 평행이동하면 된다.

$$\left[\begin{array}{cc}\cos (\alpha )& 0\\ 0& \cos (\alpha )\end{array}\right]\left[\begin{array}{cc}\cos (\alpha )& -\sin (\alpha )\\ \sin (\alpha )& \cos (\alpha )\end{array}\right]\mathbf{x}+\left[\begin{array}{c}0\\ 1\end{array}\right]$$

따라서 왼쪽 정사각형의 점은 아래와 같이 나타낼 수 있다.

$$f_1(\mathbf{x})=\left[\begin{array}{cc}{\cos }^2(\alpha )& -\cos (\alpha )\sin (\alpha )\\ \cos (\alpha )\sin (\alpha )& {\cos }^2(\alpha )\end{array}\right]\mathbf{x}+\left[\begin{array}{c}0\\ 1\end{array}\right]$$

오른쪽에 있는 정사각형의 점은 오른쪽 아래 꼭짓점 $(1,0)$을 중심으로 시계방향으로 $90^{\circ}-\alpha$ 회전변환하고 닮음비가 $\sin \alpha$인 닮음변환한 다음 $y$축 방향으로 $1$만큼 평행이동하면 된다. 다르게 말하면 $x$축 방향으로 $-1$만큼 평행이동한 점을 $(0,0)$을 중심으로 $-90^{\circ}+\alpha$만큼 회전변환한 다음 다시 $x$방향으로 $1$, $y$축 방향으로 $1$만큼 평행이동하면 된다.

$$\left[\begin{array}{cc}\cos (-{90}^{\circ }+\alpha )& 0\\ 0& \cos (-{90}^{\circ }+\alpha )\end{array}\right]\left[\begin{array}{cc}\cos (-{90}^{\circ }+\alpha )& -\sin (-{90}^{\circ }+\alpha )\\ \sin (-{90}^{\circ }+\alpha )& \cos (-{90}^{\circ }+\alpha )\end{array}\right](\mathbf{x}+\left[\begin{array}{c}-1\\ 0\end{array}\right])+\left[\begin{array}{c}1\\ 1\end{array}\right]$$

$$=\left[\begin{array}{cc}\sin (\alpha )& 0\\ 0& \sin (\alpha )\end{array}\right]\left[\begin{array}{cc}\sin (\alpha )& \cos (\alpha )\\ -\cos (\alpha )& \sin (\alpha )\end{array}\right](\mathbf{x}+\left[\begin{array}{c}-1\\ 0\end{array}\right])+\left[\begin{array}{c}1\\ 1\end{array}\right]$$

마찬가지로 오른쪽 정사각형의 점은 아래와 같이 나타낼 수 있다.

$$f_2(\mathbf{x})=\left[\begin{array}{cc}{\sin }^2(\alpha )& \cos (\alpha )\sin (\alpha )\\ -\cos (\alpha )\sin (\alpha )& {\sin }^2(\alpha )\end{array}\right]\mathbf{x}+\left[\begin{array}{c}{\cos }^2(\alpha )\\ 1+\cos (\alpha )\sin (\alpha )\end{array}\right]$$

마지막으로 아래에 있는 정사각형은 항등변환으로 나타내면 된다.

$$f_3(\mathbf{x})=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\mathbf{x}$$

http://larryriddle.agnesscott.org/ifs/pythagorean/pythTree.htm

Pythagorean Tree