코로나 19와 미분방정식

코로나 19 확진자 숫자를 예측하는 그래프는 어떻게 찾았을까? 인구나 바이러스가 늘어나는 걸 예측하는 로지스틱 모형이 있다. 

먼저 식량을 비롯한 인구 성장에 필요한 조건이 아주 좋아서 인구가 한없이 성장한다고 가정하면 인구 성장률은 인구에 비례한다. 인구는 $P$이고 단위 시간당 출생률에서 사망률을 뺀 값을 상수$k>0$로 놓자.

$$\frac{d P}{d t}=k P\tag{1}$$

이 미분방정식은 변수 분리 가능하므로 아주 간단하게 풀 수 있다.

$$\frac{1}{P} dP=k dt$$

$$\ln P=kt +C$$

$$P=Ae^{kt}\quad \quad (A=e^{C})$$

당연히 식량이나 자원은 한정되어 있으므로 인구가 지수함수로 무한하게 성장할 수 없다. 주어진 환경에서 증가할 수 있는 최대 인구를 $M$이라고 한다면 인구가 한계 상황에 가까워지면 출생률은 줄고 사망률은 늘어날 것이다. 이것을 식으로 나타내면 아래와 같다.

$$k=r(M-P)$$

여기서 $r>0$은 상수라고 할 때, 위에 있는 미분방정식 (1)을 다시 고치면 아래와 같다.

$$\frac{d P}{dt}=r(M-P)P=rMP-rMP^2\tag{2}$$

이 방정식으로 만든 모델을 로지스틱 성장(logistic growth)이라 한다. 그래프를 그리기 위해 방정식 (2)를 미분하면 아래와 같다.

$$\begin{split}\frac{d^2 P}{dt^2}&=\frac{d}{dt}(rMP-rP^2)\\ &= rM\frac{dP}{dt} -2r P \frac{dP}{dt} \\&=r(M-2P)\frac{d P}{dt}\end{split}\tag{3}$$

그래프 개형을 그려보자.

1. $P=M/2$라면 $d^2 P/dt^2=0$이다.

2. $P<M/2$라면 $M-2P>0,\;\;dP/dt>0$이므로 $d^2 P/dt^2>0$이다.

3. $M/2<P<M$라면 $M-2P<0,\;\;dP/dt>0$이므로 $d^2 P/dt^2<0$이다.

아래로 볼록하면서 증가하다가 위로 볼록하면서 증가한다.

4. $M<P$라면 $M-2P<0,\;\;dP/dt<0$이므로 $d^2 P/dt^2>0$이다. 아래로 볼록하면서 감소한다.

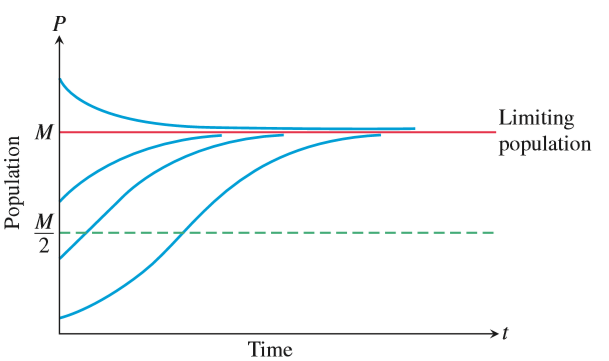
코로나 19 확진자 수도 당연히 한계가 있다. 이제 우리나라는 변곡점을 지난 것으로 보인다.

보강 2020.11.26.

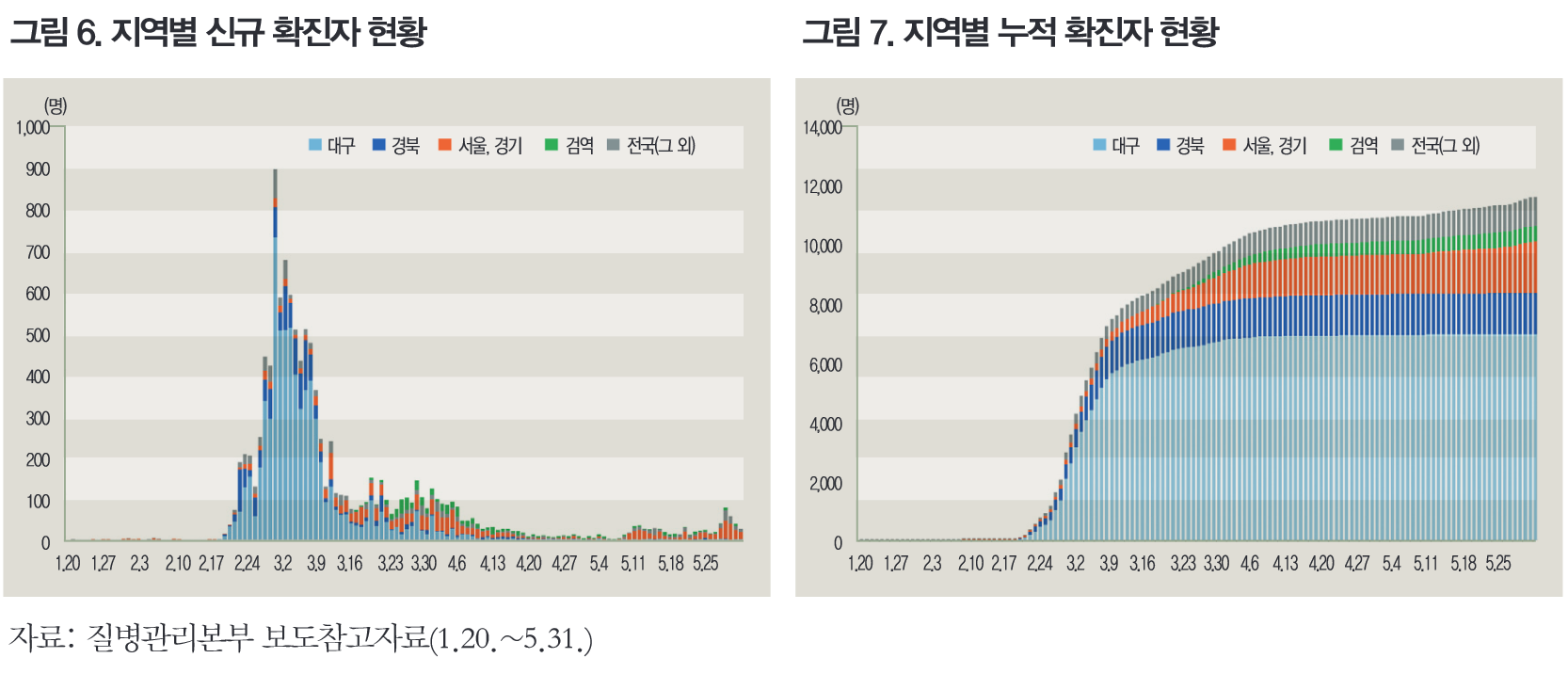
통계청에서 펴낸 파일에 있는 지난 5월 말까지 상황을 나타내는 그래프를 보면 위에서 보인 그래프와 상당히 비슷함을 알 수 있다.

3. 2020년 여름호 통계프리즘1 최바울.pdf

3.17MB

https://en.wikipedia.org/wiki/Logistic_regression

Logistic regression - Wikipedia