미분방정식 시스템과 위상 평면
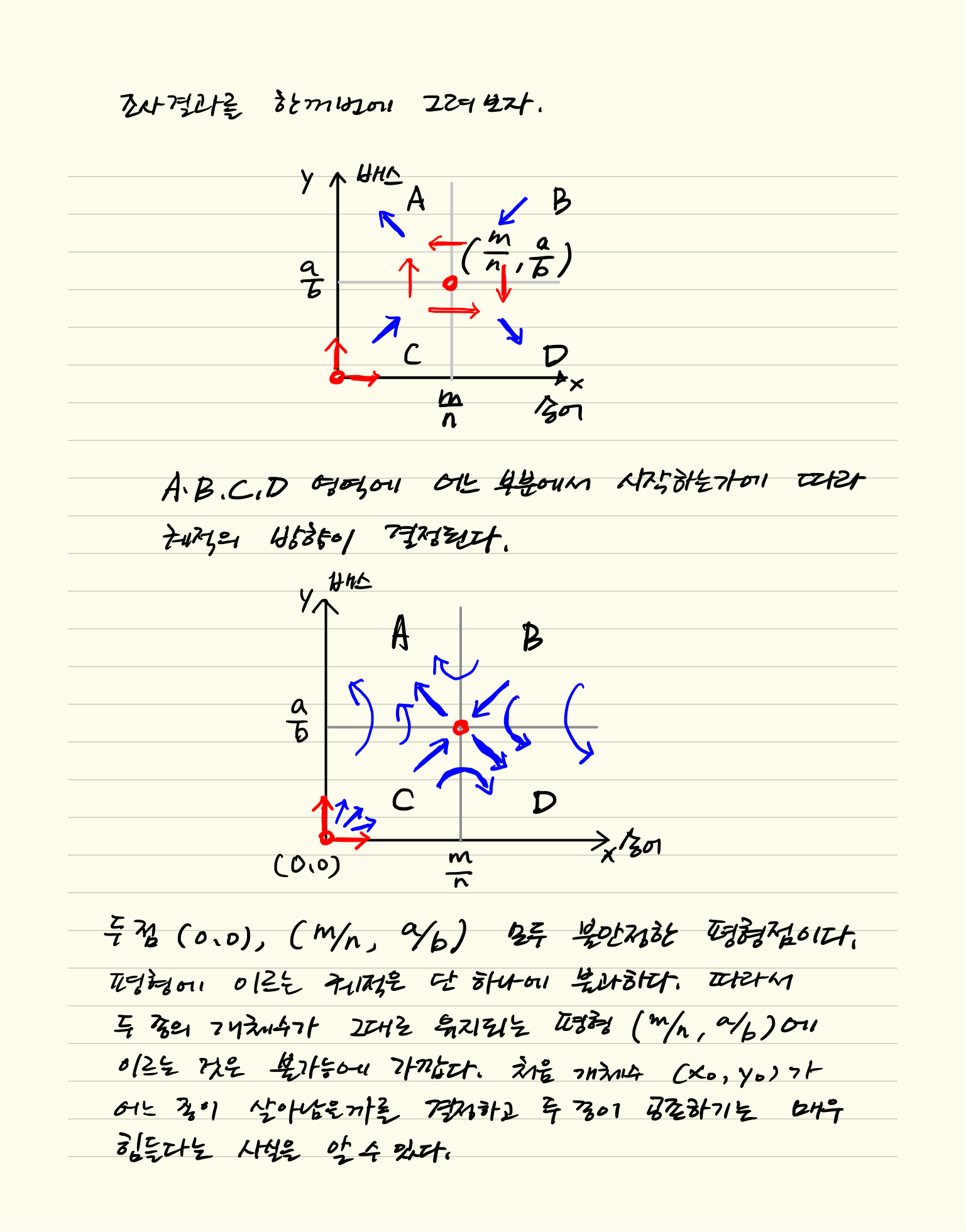
수학이야기/Calculus 2020. 7. 7. 00:54미분방정식은 특별한 모양이 아니면 해를 구하기 무척 어렵다. 하나도 풀기 어려운데 방정식이 둘 이상이라면 더욱 어렵다. 자율 방정식 풀이법을 활용하여 둘 이상의 미분방정식을 모두 만족하는 해를 찾는 방법을 소개한다. 처음이니까 위상 평면 분석법으로 1차 미분방정식이 둘인 시스템을 이해하는 방법을 적는다. 토마스 미적분학 책 9.5에 있는 글을 옮긴 것이다.




이밖에도 570페이지 연습문제에 나오는 로카-볼테라 모델도 있다. 이 모델은 토끼와 여우처럼 사냥하는 종과 희생당하는 종이 공존할 때 개체수가 어떻게 변할까를 모델로 만든 것이다. 아래 연결 고리를 따라가면 자세한 공부를 할 수 있다.
https://en.wikipedia.org/wiki/Lotka%E2%80%93Volterra_equations
Lotka–Volterra equations - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Pair of equations modelling predator-prey cycles in biology The Lotka–Volterra equations, also known as the predator–prey equations, are a pair of first-order nonlinear differentia
en.wikipedia.org
https://www.sciencedirect.com/topics/earth-and-planetary-sciences/lotka-volterra-model
Lotka-Volterra Model - an overview | ScienceDirect Topics
The result of the Lotka–Volterra model appears very “artificial” from an ecological point of view. A stable cycle is very rare in nature. Changing behavior to make it more realistic means changing the model. A fuzzy approach is much easier to underst
www.sciencedirect.com







