조화급수 Harmonic Series

조화급수는 아래와 같은데 발산하는 급수이다. 무한급수를 공부할 때 자주 나오는 급수라서 정리해 둔다.

$$\sum_{n=1}^{\infty}\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\cdots$$

조화수열은 역수가 등차수열인 수열이다. 음악에서 음은 진동수에 따라 결정되는데 기준 음보다 높은음은 현 길이에 반비례한다. 다시 말하면 음이 올라갈 때 진폭은 아래와 같은 수열을 이룬다.

$$1,\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5},\cdots$$

위와 같이 음의 조화와 관계되었기에 이름이 조화 급수인 것이다.

역사

14세기 니콜 오레즈메가 이 급수가 발산함을 증명하였으나 잊히고 말았다. 17세기에 피에트로 멘고리, 요한 베르누이와 야콥 베르누이가 새로 증명하였다. 역사적으로 건축가들이 조화수열에 관심을 가졌다. 바로크 시대 건축가들은 건축물을 자른 단면도와 입면도에 있는 비율을 만들 때와 교회나 궁전을 내부와 외부가 조화를 이루도록 건설하는데 조화수열을 사용하였다.

발산

비교 판정

아래와 같이 $2^{k-1}+1$째 항부터 $2^{k}$째 항까지 분모를 가장 큰 수인 $2^k$로 바꾼 급수와 비교해 보자. 

$$\begin{align} &{} 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8} + \frac{1}{9} + \cdots \\[12pt] \ge {} &1 + \frac{1}{2} + \frac{1}{\mathbf{4}} + \frac{1}{4} + \frac{1}{\mathbf{8}} + \frac{1}{\mathbf{8}} + \frac{1}{\mathbf{8}} + \frac{1}{8} + \frac{1}{\mathbf{16}} + \cdots \end{align} $$

두 번째 급수를 아래와 같이 더해 보면 발산함을 쉽게 알 수 있다. 따라서 조화급수는 비교 판정에 따라 발산한다.

$$\begin{align} &{} 1 + \left(\frac{1}{2}\right) + \left(\frac{1}{4}\!+\!\frac{1}{4}\right) + \left(\frac{1}{8}\!+\!\frac{1}{8}\!+\!\frac{1}{8}\!+\!\frac{1}{8}\right) + \left(\frac{1}{16}\!+\!\cdots\!+\!\frac{1}{16}\right) + \cdots \\[12pt] ={} &1 + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \cdots = \infty \end{align} $$

더 엄밀하게 표현하려면 아래와 같이 부분합을 정리하면 된다.

모든 양의 정수 $k$에서 아래가 성립한다.

$$\sum_{n=1}^{2^k} \frac{1}{n} \geq 1 + \frac{k}{2} $$

이 증명은 위에 적은 대로 1350년 니콜레 오레즈메가 제안했다. 학교에서 주로 배우는 증명이다.

적분 판정

조화급수는 아래 그림에 있는 노란 직사각형 넓이를 차례대로 더해 나가는 급수다.

 

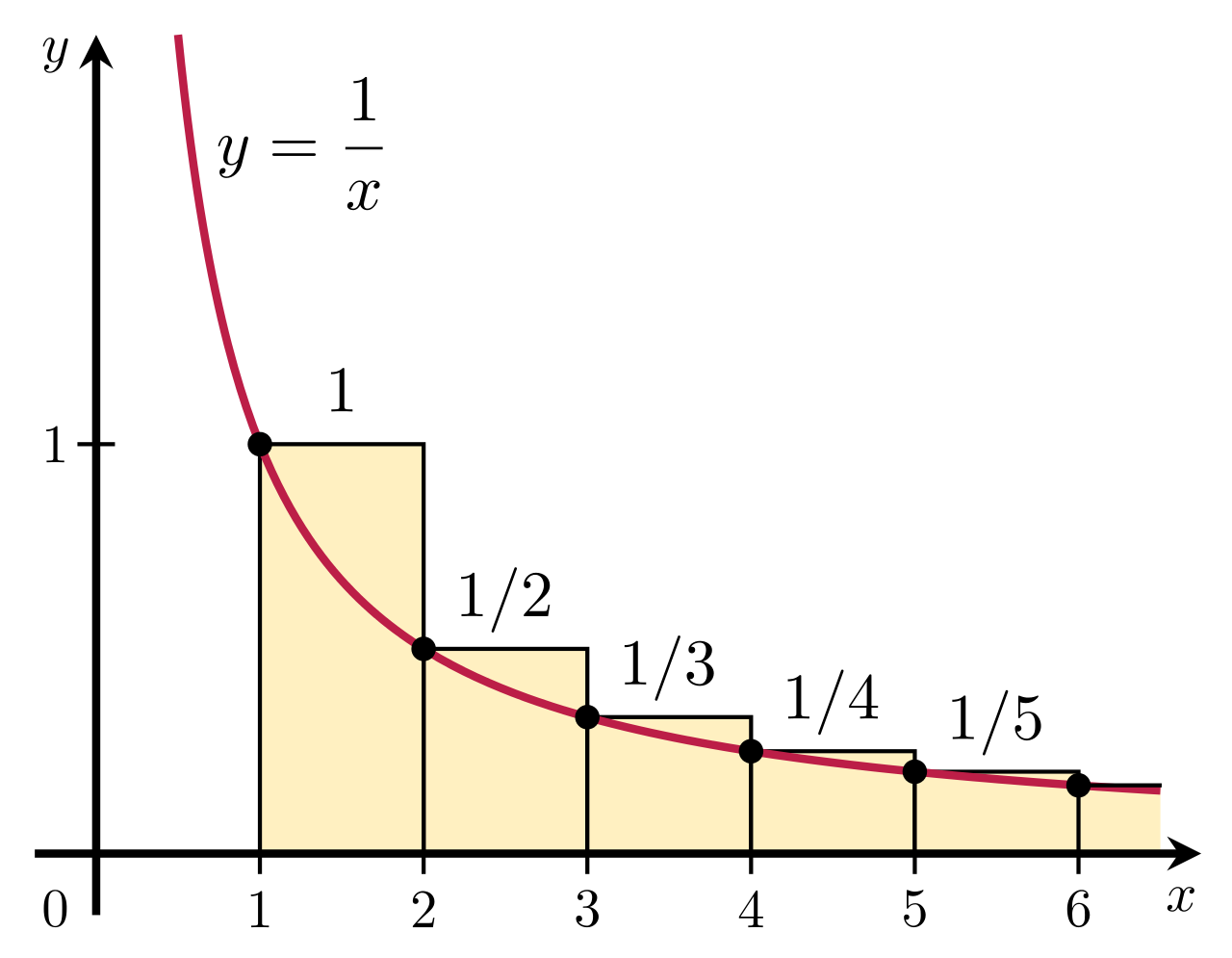
곡선 $\displaystyle{y=\frac{1}{x}}$ 아래 넓이를 이상적분으로 구하면 $\displaystyle{\int_{1}^{\infty}\frac{1}{x}dx=\lim_{n\rightarrow\infty}\ln n=\infty}$이다.

그러므로 적분 판정으로 발산함을 보일 수 있다. 엄밀하게 표현해 보자.

$$\sum_{n=1}^{\infty}\frac{1}{n}>\int_{1}^{k+1}\frac{1}{x}dx=\ln(k+1)$$

부분합

아래와 같은 조화급수의 부분합을 조화수로 부른다.

$$H_n =\sum_{k=1}^{n} \frac{1}{n}$$

조화수 $H_n$과 $\ln n$의 차 $H_n -\ln n$은 오일러-마스케로니 상수로 수렴한다.

닮은 꼴 급수

교대조화급수

아래와 같은 교대조화급수alternating harmonic series도 있는데 이 급수는 수렴한다. 

$$\sum_{n=1}^{\infty}(-1)^{n+1}\frac{1}{n}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots+(-1)^{n+1}\frac{1}{n}+\cdots$$

이 급수는 교대급수 판정으로 수렴함을 알 수 있고 테일러 급수로 극한값이 $\ln2$임을 구할 수 있다.

---

더 자세히 보기

• 음_{musical tone}
• 진동수_frequency 
• 높은음_overtune 
• 니콜레 오레즈메_{Nicole Oresme} 
• 피에트로 멘고리_{Pietro Mengoli} 
• 요한 베르누이_{Johann Bernoulli} 
• 야콥 베르누이_{Jacob Bernoulli} 
• 비교판정_{comparison test} 
• 적분판정_{integral test} 
• 오일러-마스케로니 상수_{Euler-Mascheroni constant} 
• 교대급수판정_{alternating test} 

---

https://en.wikipedia.org/wiki/Harmonic_series_(mathematics)

Harmonic series (mathematics) - Wikipedia