적분으로 무한급수가 수렴함을 판정
수학이야기/Calculus 2020. 7. 9. 22:06반응형
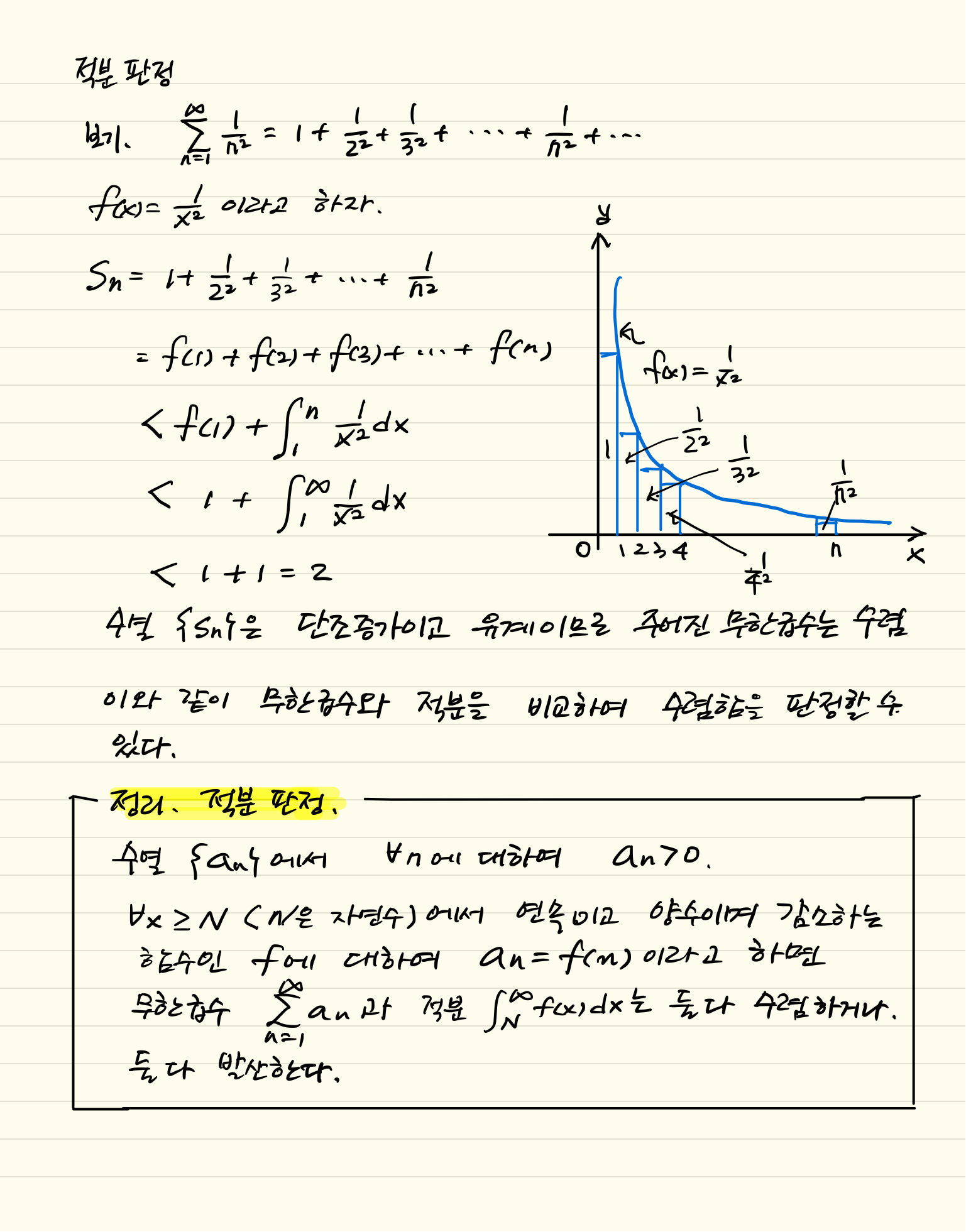
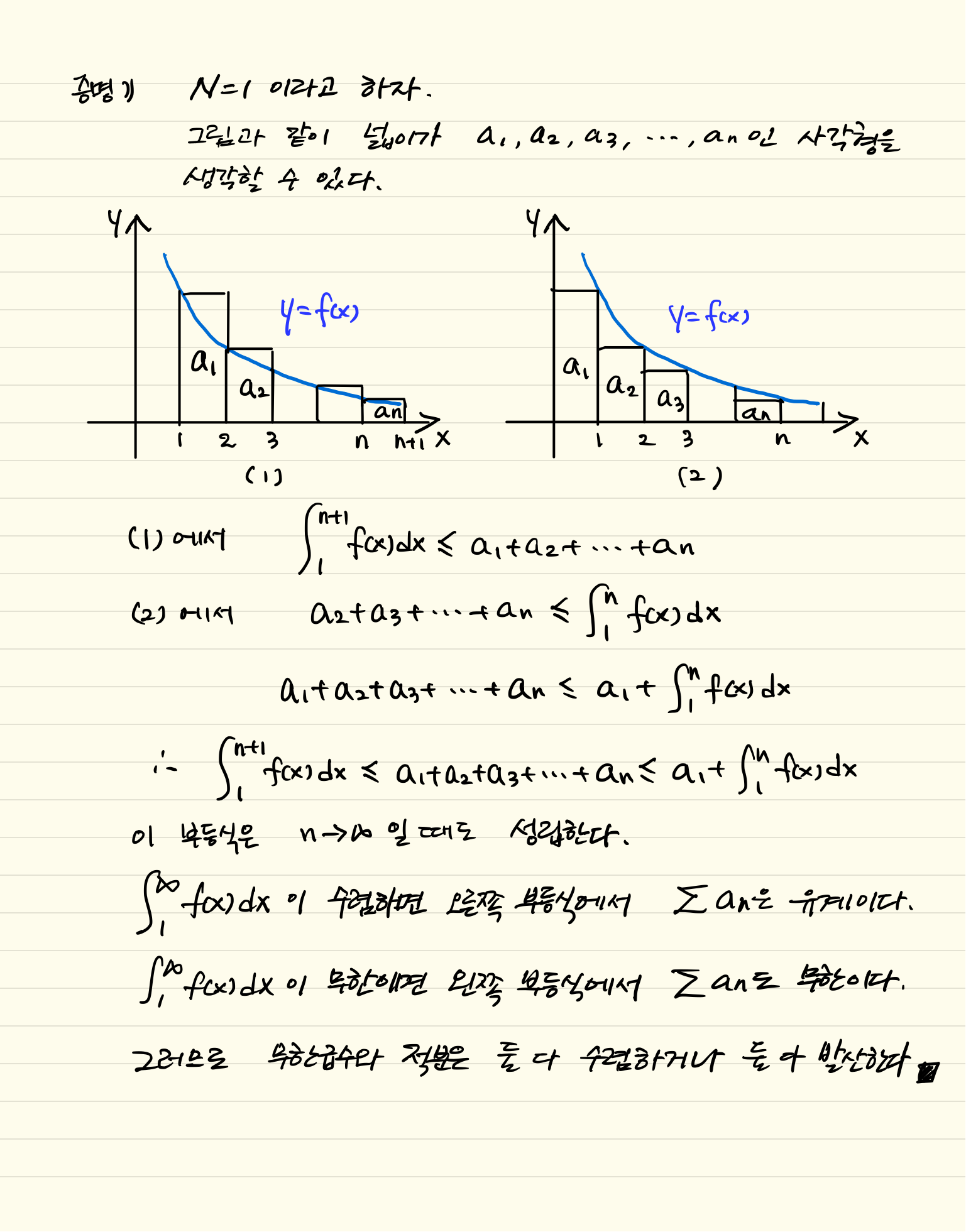
보기 아래와 같은 p-급수는 $p>1$이면 수렴하고 $p\leq1$이면 발산한다.(p는 실수)
$$\sum_{n=1}^{\infty}\frac{1}{n^p}= \frac{1}{1^P}+\frac{1}{2^p}+\frac{1}{3^p}+\cdots+\frac{1}{n^p}+\cdots$$
참고: 위에 있는 무한급수 $\displaystyle{\sum_{n=1}^{\infty}\frac{1}{n^2}}$은 아주 널리 알려진 문제다. 이 문제를 해결한 오일러를 기리기 위해 고향인 바젤을 붙여서 바젤 문제라고 부르기도 한다. 아래 글을 참고하면 수렴하는 값을 구할 수 있다.
리만 제타함수로 $\sum_{n=1}^{\infty}\frac{1}{n^2}$ 계산하기
잠깐 숨을 고르고 세상에서 가장 아름다운 수식인 오일러 항등식을 생각하자. $$e^{i\theta}=\cos\theta +i\sin\theta$$ 오일러가 생각하였다는 또 다른 방법도 있다. 알면 알수록 오일러는 천재다. 계수가
suhak.tistory.com
바젤 문제 기하로 다가서기
$$\sum_{n=1}^{\infty}=1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\cdots$$ 위에 있는 무한급수는 수렴함을 알고 있다. 이 급수가 수렴하는 값을 구하는 문제는 이탈리아 수학자 Pietro Mengoli가 1650년에..
suhak.tistory.com
반응형







