2020학년도 서울대 면접 수학 기출문제_03

문제 1 곡선 C와 직선 $l$이 점 A에서 만나고 점 A에서의 곡선 C에 대한 접선이 직선 $l$과 수직일 때 C와 점 A에서 수직으로 만난다고 한다. 곡선 $y=x^3$을 T라고 하자.

1-1. 좌표평면 위의 한 점 $(a,b)$를 지나는 직선 $l$이 점 $P(t,t^3)$에서 곡선 T와 수직으로 만날 때, $a,\;b,\;t$사이의 관계식을 $t$에 대한 다항식으로 구하시오. 또한, 곡선 T와 직선 $l$이 수직으로 만날 수 있는 점은 많아야 하나임을 설명하시오.(단, $t$는 0이 아닌 실수)

1-2. 점 $(a,b)$가 제4 사분면에 속할 때, 점 $(a,b)$를 지나고 제1 사분면 위의 점에서 곡선 T와 수직으로 만나는 직선의 개수를 구하시오.

1-3. 점 $A(-1,-1)$에서 곡선 T와 수직으로 만나는 직선 $l_1$과, 점 $B\displaystyle{\bigg(\frac{1}{5},-\frac{7}{5}\bigg)}$를 지나고 T에 접하는 직선 $l_2$ 및 곡선 T로 둘러싸인 도형의 넓이를 구하시오.

1-4. 곡선 T 위의 점 $A_1(t,t^3)$을 지나 점 $A_2$ (단, $A_1 \not=A_2$)에서 곡선 T에 접하는 직선을 $l_1$이라고 하자. 단, $t$는 양의 실수이다. 이번에는 점 $A_2$를 지나 점 $A_3$ (단, $A_2 \not=A_3$)에서 곡선 T에 접하는 직선을 $l_2$라고 하자. 이러한 시행을 반복하여 점 $A_1 ,A_2 , A_3 , \cdots$과 직선 $l_1 , l_2 ,l_3 ,\cdots$을 얻었을 때, 곡선 T와 접선 $l_n$으로 둘러싸인 도형의 넓이를 $S_n$이라고 하자.(단, $n$은 자연수). 이때, $$\sum_{n=1}^{\infty}S_n =1$$ 을 만족하는 $t$의 값을 구하시오.

풀이

1-1. 점 $P(t,t^3)$에서의 법선이 점 $(a,b)$를 지난다고 생각하면 직선 $l$을 구할 수 있다. $P$에서 접선의 기울기는 $3t^2$이므로 법선의 방정식은

$$y-t^3 =-\frac{1}{3t^2}(x-t)$$

이 직선 위에 $(a,b)$가 있다.

$$b-t^3 =-\frac{1}{3t^2}(a-t)$$

정리하면

$$3t^5 -3bt^2 +t-a=0\tag{1}$$

곡선 T와 직선 $l$이 수직으로 만나는 점은 하나임은 아래 그림에서 바로 확인할 수 있다. 간단하게 설명하자면 함수 $y=x^3$는 실수 전체에서 증가하는 1-1대응 함수이므로 수직으로 만나는 점이 둘 이상이 될 수 없다.

1-2. 점 $(a,b)$가 제4 사분면 위에 있다면 $a>0$이고 $b<0$이다.

(1)을 정리하면 $a(t)=3t^5 -3bt^2+t$로 생각할 수 있다. $t>0$이라면

$$\frac{da}{dt}=15t^4 -6bt+1>0$$

이다. $a(0)=0$이고 증가하므로 방정식 (1)의 근은 단 하나다. 따라서 구하고자 하는 직선의 개수도 하나다.

1-3. 먼저 $A(-1,-1)$에서 법선의 방정식은

$$y-(-1)=-\frac{1}{3}(x-(-1))\quad\Rightarrow\quad l_1:\;\;x+3y+4=0$$

점 $B\displaystyle{\bigg(\frac{1}{5},-\frac{7}{5}\bigg)}$를 지나고 $(s,s^3)$에서 T와 접하는 직선의 방정식을 구해보자.

$$y-s^3 =3s^2(x-s)\tag{2}$$

$$-\frac{7}{5}-s^3 =3s^2(\frac{1}{5}-s)$$

정리하면

$$10s^3-3s^2 -7=(s-1)(10s^2 +7s+7)=0$$

접점은 $(1,1)$이고 직선의 방정식은 $l_2:\;\;3x-y-2=0$이다.

한편 $B$는 $l_1$위에 있다.

$y=x^3$이 원점에 대하여 대칭인 곡선이므로 아래 그림과 같은 구하고자 하는 영역의 넓이는 직사각형 넓이의 1/2임을 쉽게 알 수 있다. 사실 대칭성을 쓰면 접점 $(1,1)$도 바로 구할 수 있다.

 

$$\therefore\;\;\frac{1}{2}\sqrt{\bigg(-1-\frac{1}{5}\bigg)^2+\bigg(-1+\frac{7}{5}\bigg)^2}\sqrt{\bigg(1-\frac{1}{5}\bigg)^2+\bigg(1+\frac{7}{5}\bigg)^2}=\frac{1}{2}\times \frac{\sqrt {40}}{5}\times \frac{\sqrt {160}}{5}=\frac{8}{5}$$

1-4. $A_1(t,t^3)$, $A_2(s,s^3)$이라고 하자. 방정식 (1)과 같은 $A_2$에서의 접선이 $A_1$을 지난다고 하자.

$$t^3 -s^3=3s^2(t-s)$$

$$(t-s)(t^2+st +s^2)=3s^2(t-s)$$

인수분해하여 정리하면

$$(t-s)^2 (t+2s)=0$$

두 점이 서로 다르므로 $s\not=t$이다. 따라서 $$s=-\frac{1}{2}t$$

따라서 점 $A_n$의 $x$좌표를 $x_n$이라고 하면 아래와 같은 점화식을 얻을 수 있다.

$$x_{n+1} =-\frac{1}{2} x_n$$ 따라서 일반항은

$$x_n =\bigg(-\frac{1}{2} \bigg)^{n-1}t\tag{3}$$

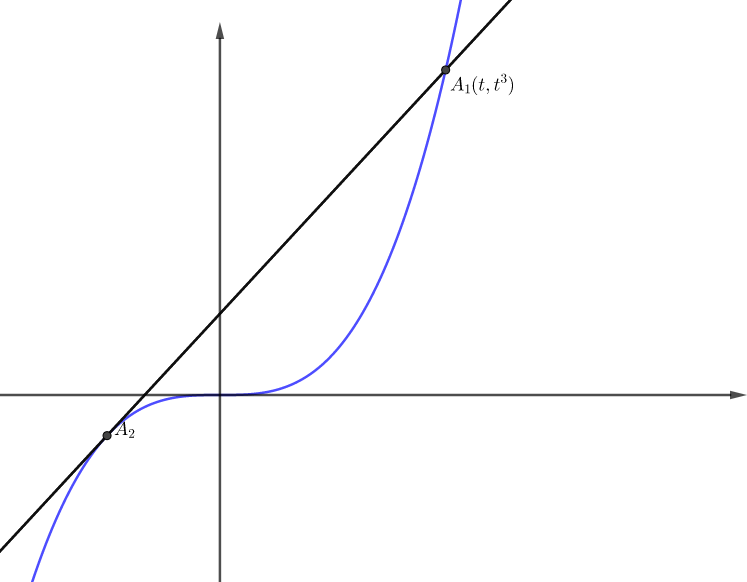
두 점 $A_n(x_n,x_n^3)$과 $\displaystyle{A_{n+1}(x_{n+1},x_{n+1}^3)=\bigg(-\frac{x_n}{2},-\frac{x_n}{8}\bigg)}$을 지나는 직선 $l_n$의 방정식은

$$y=\frac{3}{4}x_n^2 x +\frac{1}{4}x_n$$

직선 $l_n$과 곡선 T 사이의 넓이는 적분하는 방향을 고려하면 구간 $[x_n,x_{n+1}]$에서 아래와 같이 정적분하여 얻을 수 있다. $n$이 홀수일 때 직선 $l_n$이 곡선 T보다 위쪽에 있으므로 $x^3 -l_n<0$이므로 아래끝과 위끝을 바꾸면 된다.

$$\begin{split}S_n=&\int_{x^n}^{x_{n+1}} (x^3 -l_n)dx\\ =&\int_{x^n}^{-x_n /2} (x^3 -\frac{3}{4}x_n^2 x -\frac{1}{4}x_n)dx\\ =&\bigg[ \frac{1}{4}x^4 - \frac{3}{8}x_n^2 x^2 +\frac{1}{4}x_nx\bigg]_{x_n}^{-x_n/2}=\frac{27}{64}x_n^4\end{split}$$

(3)을 대입하여 정리하면

$$S_n=\frac{27}{64}x_n^4 =\frac{27}{64}\cdot \bigg(-\frac{1}{2}\bigg)^{4n-4}t^4 =\frac{27}{64}\cdot\bigg(\frac{1}{16}\bigg)^{n-1}t^4$$

마지막으로 무한급수를 계산하자.

$$\sum_{n=1}^{\infty}S_n=\sum_{n=1}^{\infty}\frac{27}{64}\cdot\bigg(\frac{1}{16}\bigg)^{n-1}t^4=\frac{27t^4/64}{1-1/16}=\frac{9}{20}t^4$$

이 값이 $1$이 되는 $t$를 계산하면

$$t=\sqrt[4]{\frac{20}{9}}$$

 

admission.snu.ac.kr/undergraduate/notice?md=v&bbsidx=127422

2020학년도 서울대학교 입학전형 선행학습 영향평가 - 공지사항 - 대학 - 입학 - 서울대학교 입학�