비례와 반비례

중학교 1학년에서 비례와 반비례를 배운다. 하지만 수학에 관심을 가지고 있는 학생도 정작 비례와 반비례를 정확하게 알지 못하는 경우가 매우 많다. 아마도 꼼꼼하게 그 뜻을 살피지 않고 대충 넘어간 탓일 것이다. 하물며 수학에 큰 관심을 가지지 않은 이들은 일상 속에서 비례와 반비례를 잘못 알고 쓰는 일이 자주 일어난다.

아주 흔한 잘못은 $x$가 증가할 때 $y$도 같이 증가하면 비례이고 $y$가 감소하면 반비례라고 말하는 것이다. 사실 비례와 반비례는 증가, 감소와 전혀 상관없는 말이다. 그렇다면 정확한 비례와 반비례의 뜻은 무엇일까?

먼저 비례는 두 변수 $x$와 $y$의 비가 상수인 것이다. 상수는 다른 말로는 일정한 값이라고 할 수 있다. 식으로 표현하면 아래와 같다.

$$y:x=a:1\;\;,\quad\quad y=ax\;\;,\quad\quad \frac{y}{x}=a$$  

여기서 당연히 $a\not =0$이다.

반비례는 어떤 변수가 다른 변수의 역수와 비례할 때를 말한다. 식으로 적는다면 아래와 같다.

$$y:\frac{1}{x}=a:1\;\;,\quad\quad y=\frac{a}{x} \;\;,\quad\quad xy=a$$  

그렇다면 왜 많은 이들이 비례와 반비례를 잘못 알고 있을까? 아마도 중학교 교과서에 비례와 반비례를 아래와 같이 설명하고 있기 때문일 것이다.

두 변수 $x,\;\;y$에 대하여 $x$의 값이 2배, 3배, 4배, $\cdots$로 변함에 따라 $y$의 값도 2배, 3배, 4배, $\cdots$로 변할 때, $y$는 $x$에 정비례한다고 한다.

두 변수 $x,\;\;y$에 대하여 $x$의 값이 2배, 3배, 4배, $\cdots$로 변함에 따라 $y$의 값이 $\displaystyle{\frac{1}{2}}$배, $\displaystyle{\frac{1}{3}}$배, $\displaystyle{\frac{1}{4}}$배, $\cdots$로 변할 때, $y$는 $x$에 반비례한다고 한다.

$y$의 값이 2배, 3배, 4배로 변한다는 것을 늘어난다고 오해하는 것이다. 위에 적은 두 변수 $x,y$가 서로 비례할 때를 나타내는 식에서 $y=ax$에서 $a>0$일 때만 생각하는 잘못을 저지르고 있는 이가 많다. 반비례도 마찬가지다.

학생들이 진학을 했을 때를 위해 중학교 교과서에서 표현을 가다듬어야 할 까닭이 여기에 있다. 물론 지금도 교과서에 그래프로 $a<0$일 때를 언급하고는 있다. 중학교 과학에선 속력과 이동거리와 같이 양수인 변수를 다루기 때문에 잘못된 개념을 만들고 있는 듯도 하다. 그렇다고 방향을 바꾸는 운동처럼 복잡한 문제로 속도를 가르치기엔 중학생은 너무 어리다.

지금 중학교 1학년 학생이라면 아래와 같이 정확하게 그래프로 이해하고 있어야 한다.

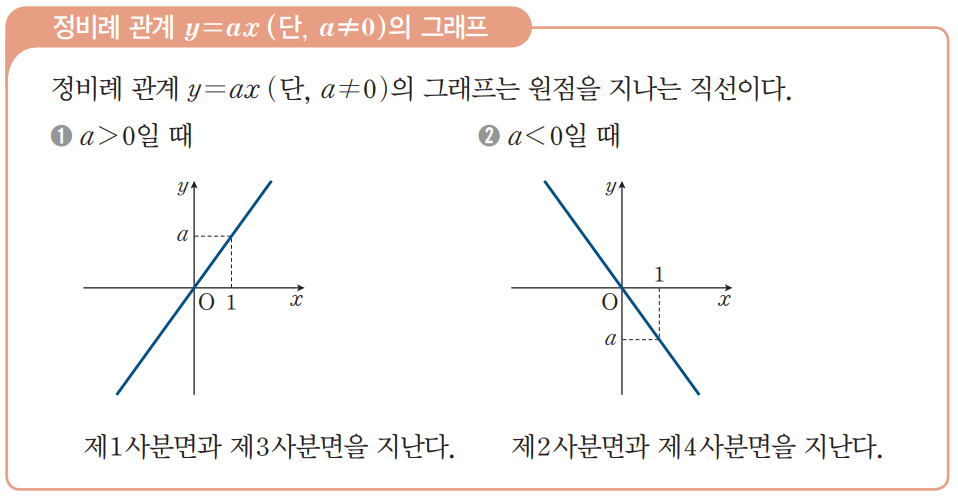
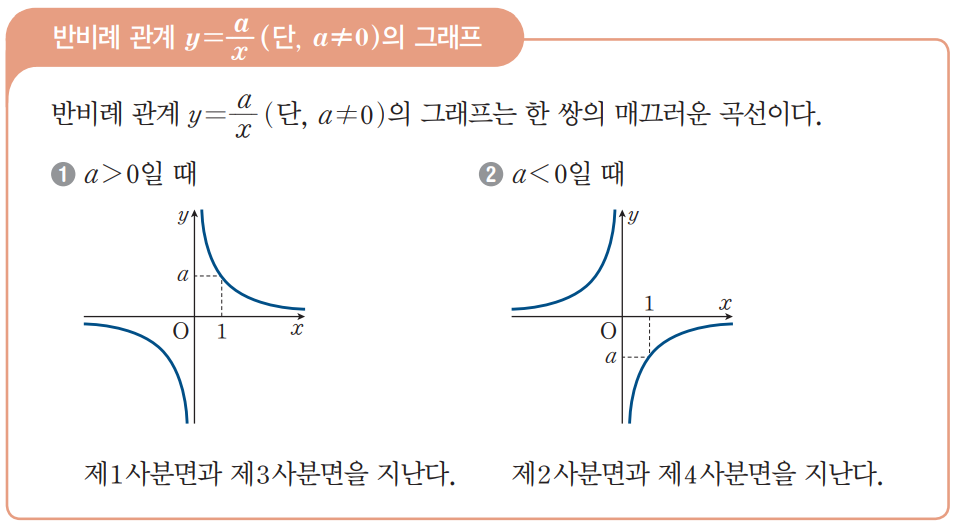
수학과 과학에 등장하는 수많은 비례상수는 바로 여기에 언급하는 비례 관계를 알려주는 상수인 것이다.

예를 들면 원둘레 $l$는 지름 $2r$과 비례하고 넓이 $A$는 반지름의 제곱 $r^2$과 비례하는데 이때 비례 상수가 바로 원주율 $\pi$이다.

$$l=2\pi r\;\;,\quad\quad A=\pi r^2$$

물리에선 만유인력 상수 $G$가 가장 먼저 떠오른다. 만유인력은 모든 물체 사이에 작용하는 서로를 끌어당기는 힘이다. 이 힘($F$)은 두 물체의 질량($m_1 , m_2$)을 곱한 값에 비례하고 두 물체 사이 거리($r$)의 제곱에 반비례한다. 식으로 나타내면 아래와 같다.

$$F=G\frac{m_1 m_2}{r^2}$$

경제 분야에선 나라와 나라의 돈을 바꾸는 비율인 환율이 대표적인 비례 상수다. 물론 환율이 수시로 변해서 상수란 느낌이 들지 않지만 말이다.

비례는 영어로 proportionality이다. 영어에 자신이 있다면 아래 글을 참고하시라.

https://en.wikipedia.org/wiki/Proportionality_(mathematics) 

Proportionality (mathematics) - Wikipedia