부등식이란 무엇인가?

고등학교에서 오래 수학을 가르친 까닭에 중학교에 와서 자꾸 어렵게 가르친다. 아무래도 먼저 명확하게 정의를 내리고 그 정의에 따르는 정리를 가르치는 것이 익숙해서 좀처럼 벗어나지 못한다. 그냥 쉽게 교과서에 있는 내용만 설명하고 나면 뭔가 아쉽다. 새로 부등식 단원을 시작하면서도 마찬가지다.

중학교 교과서는 '부등식은 부등호($<,\;\;>,\;\; \leq, \;\; \geq$)를 써서 수 또는 식의 대소 관계를 나타낸 식'이라고 적고 있다. 아래는 모두 부등식이다.

$$2<5,\;\;x<1,\;\;a+5 \leq 2,\;\;2x+3<x+1$$

학생 대부분은 이야기를 덧붙이지 않아도 직관적으로 대소 관계를 알 수 있다. 그런데 부등호에 대한 정의를 덧붙이지 않으면 뭔가 찜찜하다.

부등호는 중학교 1학년, 부등식은 중학교 2학년에 처음 등장하는데 사실 고등학생도 부등호를 명확하게 정의하지 못하는 일이 많다. 쓸데없어 보이지만 부등호를 정의해 보기로 하자. 복소수를 배우기 전까지 배우는 모든 수는 순서가 매겨져 있어서 모두 수직선 위에 나타낼 수 있다. 참고 중학교 1학년은 정수와 유리수, 3학년은 무리수와 실수를 배운다. 따라서 중학 과정에서 모든 수는 실수라고 보아야 한다.

이 글은 중학교 2학년을 대상으로 하므로 모든 수는 유리수를 뜻한다고 생각하자. 아래에 수직선이 있다. 수직선에서 화살표는 양의 방향을 의미한다. 따라서 유리수를 수직선 위에 나타냈을 때 오른쪽에 있는 수가 왼쪽에 있는 수보다 크다.

예를 들면

$$-2<3,\;\;\frac{1}{3}<\frac{1}{2},\;\;-3.5<-2.4$$이다. 이와 같이 대소 관계를 따지는 일은 매우 번거롭다. 따라서 부등호를 엄밀하게 정의할 필요가 있다. 먼저 두 유리수 $a,\;b$가 있을 때 $a-b$도 유리수이다. 유리수는 반드시 양수($+$), $0$, 음수($-$) 가운데 하나가 된다. 편하게 '양수$>0$', '음수$<0$'으로 나타내기로 하자.

부등호의 정의

$a,\;b$가 유리수일 때,
\begin{align} a-b>0 \quad \iff \quad a>b \tag{1} \\ a-b=0 \quad \iff \quad a=b\tag{2} \\ a-b<0 \quad \iff \quad a<b  \tag{3} \end{align}

괜히 어렵게 적은 것처럼 느껴질 것이다. 위에 있는 정의는 두 수의 대소 관계를 비교할 때는 빼서 양수인가 음수인가 알아 보면 된다는 말이다.

$$\frac{1}{2}-\frac{1}{3}=\frac{1}{6}>0$$이다. 따라서 $$\frac{1}{2}>\frac{1}{3}$$이다.

예제. 두 유리수 $\displaystyle{\frac{6}{13},\;\;\frac{3}{7}}$은 어느 것이 더 큰가?

$$\frac{6}{13}-\frac{3}{7}=\frac{42-39}{91}>0$$이므로 $$\frac{6}{13}>\frac{3}{7}$$이다. 분모가 다른 두 수의 크기를 비교하기 위해 통분을 하는 까닭을 자연스럽게 깨닫게 된다.

문제 다음에 있는 수를 큰 것부터 차례로 적어 보아라.

$$0.\dot{3}\dot{6},\;\; \displaystyle{\frac{1}{3}},\;\;\frac{13}{33},\;\;0.35$$ 

부등식의 정의

부등식은 부등호($<\;,\;\;>\;,\;\; \leq\;, \;\; \geq$)를 써서 수 또는 식의 대소 관계를 나타낸 식

수와 수 사이의 대소 관계는 문제로 다룰 필요가 거의 없다. 따라서 교과서에서 배우는 부등식은 대부분 문자가 들어 있는 식의 대소 관계를 나타낸다. 특히, 1학년에서 배운 방정식과 마찬가지로 문자 $x$가 들어 있는 식을 주로 다룬다. 예를 들면 아래와 같다.

$$2x+1>0,\;\;2x+3<x-2$$

부등식 $2x+3>7$이 있다. 이 부등식의 $x$에 $0,\;\;1,\;,\;2,\;\;3\;\;4$를 대입해 보자.

$$2\times 0+3=3\not>7$$

$$2\times 1+3=5\not>7$$

$$2\times 2+3=7\not>7$$

$$2\times 3+3=9>7$$

$$2\times 4+3=11>7$$

$3,\;\;4$처럼 주어진 부등식을 참이 되게 하는 미지수의 값을 그 부등식의 해라고 하고 부등식의 해를 모두 구하는 것을 부등식을 푼다고 한다.

부등식의 성질

부등식 $2<4$의 양변에 같은 수를 덧셈, 뺄셈, 곱셈, 나눗셈을 했을 때 어떻게 되는가 살펴서 성질을 파악할 수 있다. 등호와 달리 부등호는 방향이 있어서 부등식은 등식과 성질이 다른 부분이 있다.

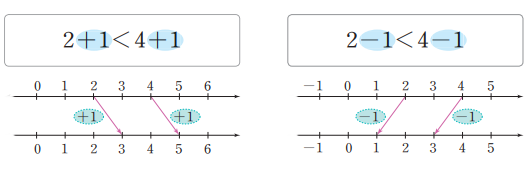
1. 덧셈과 뺄셈 

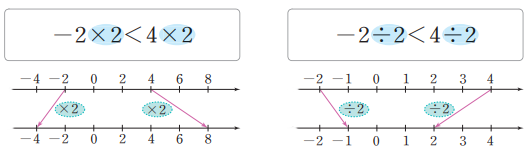
2. 양수의 곱셈과 나눗셈

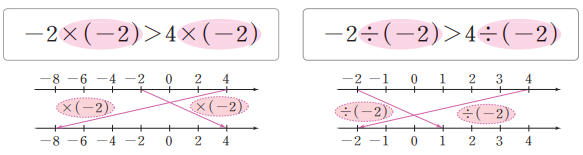
3. 음수의 곱셈과 나눗셈

부등식의 성질
1. 부등식의 양변에 같은 수를 더하거나 양변에서 같은 수를 빼어도 부등호의 방향은 바뀌지 않는다.
$$a<b \;\;\Rightarrow \;\; a+c<b+c,\;\;a-c<b-c$$

2. 부등식의 양변에 같은 양수를 곱하거나 양변을 같은 양수로 나누어도 부등호의 방향은 바뀌지 않는다.
$$a<b,\;\;c>0 \;\;\Rightarrow \;\;   ac<bc,\;\;\displaystyle{\frac{a}{c}<\frac{b}{c}}$$

3. 부등식의 양변에 같은 음수를 곱하거나 양변을 같은 음수로 나누면 부등호의 방향은 바뀐다.
$$a<b,\;\;c<0\;\;\Rightarrow \;\;   ac>bc,\;\;\displaystyle{\frac{a}{c}>\frac{b}{c}}$$

3번 성질을 자세하게 살펴보자.

$a<b$이면 $a-b<0$ 다시 말하면 $a-b$는 음수이다.

여기에 $c<0$이므로 $(a-b)c>0$이다.

전개하면 $ac-bc>0$이므로 $ac>bc$이다. 

나눗셈은 역수를 곱하는 것과 같으므로 결과는 같다.

음수를 곱하면 부호가 바뀌므로 당연히 부등호 방향도 바뀌어야 한다고 기억해서 실수가 없도록 하면 된다.

등식의 성질을 이용하여 방정식을 풀듯이 부등식의 성질을 이용하여 부등식을 풀 수 있다. 하지만 매번 성질을 되새기며 계산하기 번거로우므로 간단하게 덧셈과 뺄셈은 이항하면 부호가 바꾼다고 생각하고 곱셈과 나눗셈은 역수를 곱한다고 생각해서 해결한다.

 

 

---

참고

부등호 $<$와 $>$는 영국의 수학자 해리엇(Harriot. T.. 1560~1621)이 처음 사용하였고, 등호가 결합된 부등호 $\leqq$와 $\geqq$는 프랑스의 과학자 부게르(Bougure. P.. 1698~1758)가 처음 사용하였다. 우리나라 중등 수학책에서 80년대까지는 $\leqq$와 $\geqq$를 쓰다가 이제는 $\leq$와 $\geq$로 적는다. 이렇게 함으로써 수학책 인쇄에 쓰는 잉크를 절약할 수 있다. 일본은 아직도 옛날 우리나라처럼 중고교 수학책에선 두 줄을 고수하고 있다고 한다. 부등호만큼은 일제의 잔재를 버렸다고 볼 수 있다.

등식과 부등식처럼 좌변과 우변 사이의 관계를 나타내는 식을 관계식(expression of relation)이라고 한다. 고등학교에서는 문자가 들어 있는 관계식을 아래와 같이 분류한다.

$$\text{관계식}\begin{cases}\text{등식} & \begin{cases}\text{방정식}\\\text{항등식}\end{cases}\\ \text{부등식}& \begin{cases}\text{조건부등식}\\\text{절대부등식}\end{cases} \end{cases}$$