비, 율, 비율 그리고 분수

수학에서는 무엇이든 엄밀하게 구별하려고 한다. 일상에서 구별하지 않아도 문제없이 쓰이고 있는 말이라도 수학 공부할 때는 정확하게 구별해서 쓰려고 힘써야 한다. 이 글은 힘들어도 수학을 수학답게 공부하고 싶은 사람을 위한 글이다. 어차피 답만 맞으면 된다고 생각한다면 이 글을 읽을 필요가 없다. 

이제 수업 시간에 도형의 닮음을 시작하고 있다. 닮았다는 말도 일상에서 쓸 때와 수학 시간에 쓸 때 잘 구별해서 써야 한다. 그냥 비슷하게 생길 걸 닮았다고 말하면 모든 삼각형은 닮음이라고 말할 수 있다. 재미있게도 모든 삼각형을 같은 도형으로 다루는 '위상수학'도 있다.

'닮음'하면 닮음비가 중요하다. 비례식을 다루다 보면 비는 분수로 고쳐서 계산할 때가 잦다. 그러다 보면 비와 분수는 같은 말이라고 착각할 가능성이 있다. 

비(ratio), 율(rate), 비율(proportion), 분수(fraction)

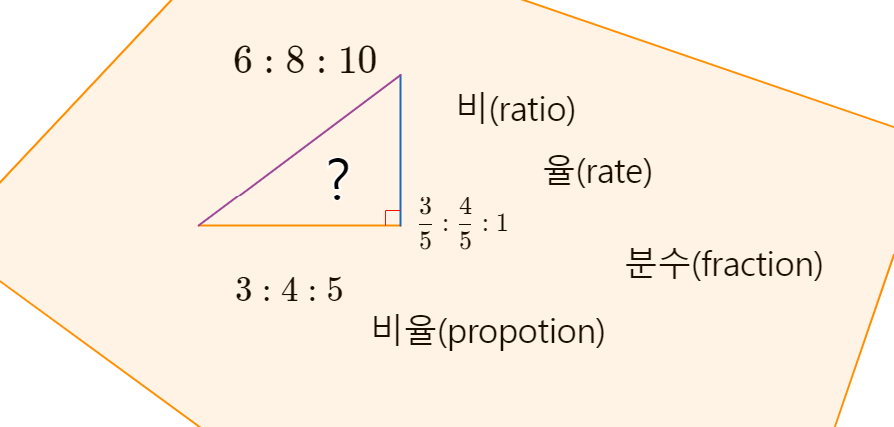
제목에 있는 말을 명확하게 구별하지 않고 쓰는 사람이 많다. 예전과 달리 이제 우리나라에서 한자로 比, 率, 比率로 적는 일은 거의 없다. 오히려 영어로 썼을 때 더 잘 구별되는 느낌이다. ratio와 rate는 같은 말뿌리일 것 같다. 일상에선 구별하지 않고 혼용해도 별 문제가 되지 않는다. 하지만 수학 시간엔 더 정확하게 쓰기 위해 정리해 본다.

1. 비(ratio): 말 그대로 개수나 양을 단순하게 나란히 놓고 비교하는 숫자를 통틀어 부르는 말이다. 유클리드는 원론 5권에서 길이와 길이 또는 넓이와 넓이처럼 같은 종류 사이의 관계만을 비(ratio)라고 정의했다.

2. 율(rate): 비(ratio)의 하위 개념으로 성질이 다른 대상을 비(ratio)로 나타낸 것이다. 기준이 되는 대상의 크기를 1, 10, 100와 같은 단위로 정해놓는다. 주로 단위 시간당 이동한 거리를 나타내는 속력이나 지도의 축척과 같은 것이다.

3.  비율(proportion): 수학적으로 같은 비는 비율이 같다고 말한다. $2:5=4:10=6:15$와 같이 비 사이의 관계를 나타낸 관계식을 비례식이라고 한다. 1을 기준으로 0.4:1과 같이 생각했을 때 0.4가 비율이다. 지도의 척도와 같이 숫자로 표현하지만 엄밀하게 따지면 수학에서 말하는 수가 아닐 수도 있다. 초등학교에서 비례배분을 배우는데 이때 쓰는 비례가 비율이다. 반드시 전체에 대한 부분을 나타내는 것이 아닐 수도 있다.

내가 적었지만 이래서 알까 싶다.

사과 6개, 자동차 4대가 있다고 하자.

사과의 개수와 자동차 개수의 비는 6:4이다. 이것을 3:2로 쓰는 것은 수학적으로 별다른 의미가 없다. 그냥 사과 개수가 자동차보다 개수가 많다를 뜻한다.

빨간 사과 6개와 푸른 사과 4개가 있다고 하자.

이때는 두 종류 사과의 개수를 비로 나타내면 6:4이다. 이것을 3:2로 쓰는 것은 사과와 자동차 개수의 비와는 다른 의미를 가진다. 이때 빨간 사과와 전체 사과의 개수를 비로 나타내면 6:10이다. 이 비는 부분과 전체의 비라는 다른 의미를 가진다. 3:5나 0.6:1은 같은 비이다. 이것을 빨간 사과가 5개 가운데 3개 꼴로 있다고 말하면 비율이라고 할 수 있다. 

시속 60Km는 무엇일까?

1시간에 60Km 꼴로 가는 빠르기를 말한다. 단위를 보면 $Km/h$로 시간에 대한 움직인 거리를 비로 나타낸 것이다. 시간과 거리는 전혀 다른 성질을 가진다. 단위까지 고려하여 60Km:1시간으로 생각하면 율이고 속력을 나타내는 숫자인 60만 따로 떼어내면 비율이다. 율과 비율을 굳이 구분할 필요가 있을까 싶다. 대체로 율(rate)은 속도, 가속도, 축척과 같이 다른 이름을 가지고 있다.

따지기 좋아하는 사람에게 듣는 핀잔을 피하려면 비율이나 율보다 몇 대 몇이면 그냥 비로 표현하는 것이 좋겠다. 율은 대체로 증가율, 변화율처럼 다른 말 뒤에 붙여서 쓰고 홀로 쓰는 일은 드물다. 원둘레와 지름의 길이가 이루는 비와 원주율을 생각하면 비와 비율을 구분할 수 있지 않을까 싶다. 황금비와 황금비율을 구분하면 좋지만 뭐 너무 따지진 말자.

분수(fraction): 전체에 대한 부분을 나타내는 비를 수로 나타낸 것이다. 누구나 알고 있듯이 분수는 전체를 나타내는 분모와 부분을 나타내는 분자로 표현한다.

마지막으로 비율과 분수는 어떻게 다를까?

분수는 수학에서 쓰는 실수(real number)이므로 반드시 서로 의미 있는 연산을 할 수 있다는 점이 비율과 다른 점이다. 어떤 비율을 분수로 나타낼 수 있다고 비율과 분수를 같은 것으로 생각하면 안 된다.

비율은 비를 나타내는 숫자이므로 연산을 하는 일이 무의미할 때가 있다. 5% 소금물 + 5% 소금물=10% 소금물과 같은 연산은 의미가 없다. 실제로 소금물 문제를 풀 때 백분율을 수로 여겨서 덧셈으로 답을 구하려는 이들이 있다.

덧붙임

초등학교에서 분수를 배울 때를 생각해 보자. 전체를 1로 놓고 등분한 조각을 나타내는 것으로 분수를 시작한다. 전체에 대한 부분을 나타내는 수이므로 분수는 1보다 작아야 한다. 전체는 부분보다 작다는 공리를 받아들인다면 말이다. 하지만 학년이 높아질수록 분수가 나타내는 수의 범위가 점점 넓어진다. 1보다 작은 진분수와 1보다 큰 가분수까지 아우르고 결국은 분모와 분자가 모두 정수인 유리수를 넘어 무리수인 것까지 분수로 부른다. 따라서 분수와 유리수가 같다고 생각하면 안 된다.

'비례한다.(proportional)'는 말도 많은 학생들이 잘못 알고 있다. '$x$와 $y$가 정비례한다.'는 어떤 뜻이냐고 물으면 $x$가 증가할 때, $y$도 증가하는 것이라고 답하는 학생들이 많다. 중학생은 물론 대학생도 많을 것이다. 일상생활에서 '키와 몸무게는 비례한다.'와 같이 쓰기 때문에 생기는 오해다. 하지만 수학 시간에 쓰는 정비례는 '비가 일정하다.'를 뜻하는 것이지 증가나 감소와는 관련 없다. 중학교 1학년 과정에서 (1)과 같이 분명하게 배운다.

$$x:y=1:a\;\;\iff \;\;y=ax \;\;(a\not=0)\tag{1}$$

이처럼 우리가 흔히 쓰는 말도 수학 시간에 사용할 때는 다른 의미를 가질 때가 있으므로 처음 배울 때 정확하게 이해하는 일이 매우 중요하다. 

Ratio - Wikipedia

Ratio - Wikipedia

Proportionality (mathematics) - Wikipedia

Proportionality (mathematics) - Wikipedia

수학용어 사용에서 드러난 비 지도에 대한 미국과 한국의 관점차 https://koreascience.kr/article/JAKO201531360572897.pdf