해밀톤 경로와 세계 일주

해밀토니안(Hamiltonian)

1857년 영국의 수학자 해밀톤은 아래와 같은 세계 일주 게임을 소개했다. 

정십이면체의 꼭짓점 20개에 세계의 이름난 도시 이름을 붙이고 어느 한 도시를 출발하여 모서리를 따라 다른 도시를 모두 방문하고 출발한 도시로 돌아오시오. 이때 한 번 지나간 도시를 다시 지날 수는 없다.

이산수학 문제는 쉬워 보이지만 막상 풀어보면 쉽지 않은 것들이 많다.

먼저 그래프에서 모든 꼭짓점을 지나는 경로는 '해밀톤 경로(Hamiltonian path)'이고 출발점과 끝점이 같으면 '해밀톤 회로(Hamiltonian circuit)'이다. 해밀턴 회로를 가진 그래프를 '해밀토니안(Hamiltonian)'으로 부른다. 어떤 그래프가 '해밀토니안'인가를 단박에 알아내기는 쉽지 않다.

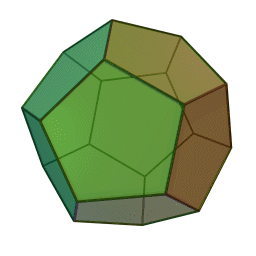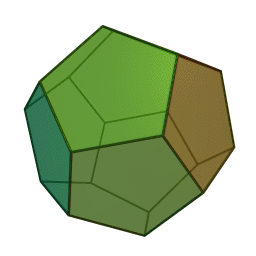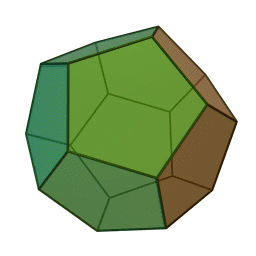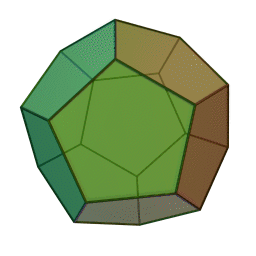
해밀톤은 입체를 아래와 같이 연결 상태가 같은 평면 그래프로 나타낸 다음 해결했다. 연결이나 연속과 같이 작은 변환에 영향을 받지 않는 기하적 성질을 연구하는 분야는 그 이름도 유명한 위상수학이다. 구와 연결 상태가 같은 다면체에서 면을 하나 잘라내고 나머지 면과 변을 늘이거나 줄여서 평면에 펼쳐 놓으면 꼭짓점과 모서리를 그대로 가지는 평면그래프가 된다.

당연히 꼭짓점과 변의 개수, 꼭짓점의 차수가 달라지지 않는다. 이 방법은 오일러 정리를 증명하는데도 아주 유용하다.

https://suhak.tistory.com/189

오일러 정리

정다면체는 아래와 같이 바꿀 수 있다.

기사의 여행(knight's tour)

해밀톤 경로와 관련된 문제 가운데 '기사의 여행'이 있다. 체스에서 기사인 말은 $L$자 모양으로 움직일 수 있다.

pixabay

아래 그림과 같이 $8\times 8$ 체스판 위에서 '기사(knight)'가 움직이는 규칙에 따라 이동하여 모든 칸을 거치는 해밀튼 경로는 모두 몇 가지일까?

n	$n\times n$ 보드에서 방향이 있는 경로의 개수(OEIS에 있는 수열 A165134)
1	1
2	0
3	0
4	0
5	1,728
6	6,637,920
7	165,575,218,320
8	19,591,828,170,979,904

 

제자리로 다시 돌아오는 경로는 닫힌 경로이고 그렇지 못하면 열린 경로이다. 이 문제에도 오일러가 푼 해가 있다. 오일러는 어디에나 있는 듯하다. 신기하게도 지나간 경로에 번호를 매기면 마방진이 되기도 한다. 아래와 같은 경로는 전체도 마방진이지만 넷으로 나눈 정사각형도 마방진이 된다.

 

https://en.wikipedia.org/wiki/Knight's_tour

Knight's tour - Wikipedia

외판원 순회 문제(TSP: travelling salesman problem)

대표적 난제로 알려진 외판원 순회 문제(TSP: travelling salesman problem)는 방향이 없고 각 변에 무게가 주어진 그래프(undirected weight graph)에서 최적의 해밀톤 회로를 찾는 문제로 생각할 수 있다. 이쯤 되면 슈퍼 컴퓨터로도 해결하기 어려운 문제가 된다. 보기엔 단순하지만 그 안에 끝을 알 수 없는 어려움을 간직한 문제...

예전에 과학고에 근무하면서 몇몇 아이들과 같이 연구했던 주제이기도 하다. 수학을 전공하는 친구는 없는데 그 친구들 아직도 수학을 좋아하고 있을까? 

https://en.wikipedia.org/wiki/Travelling_salesman_problem

Travelling salesman problem - Wikipedia

수학사랑에 도형과 그래프라는 제품이 있다. 조금 어렵지만 중학교 학생과 같이 해도 된다. 중학교 2학년 학생들과 같이 해보았는데 대부분은 한붓그리기에서 탈락하고 말지만 끝까지 해내려고 열심히 하는 학생도 많았다. 다른 제품에 비해 값이 싸서 좋다. 다만 조금 경로와 회로를 엄밀하게 구분하지 않고 사용하고 있다. 사실 이글은 교재의 부족한 부분을 채우려고 쓴다.

https://shop.mathlove.kr/shop/goods/goods_view.php?goodsno=4527 

수학사랑 쇼핑몰