대수막대로 알아 보는 인수분해

중학교에서 배우는 인수분해는 주로 2차 다항식을 다룬다. 따라서 넓이와 관련된 문제로 바꿔서 생각하면 쉽게 이해할 수 있다. 아래와 같이 수학 원리를 따져보는 사각형을 대수막대라고 부른다.

곱셈공식을 외우고 역으로 인수분해 공식을 외우면 간단하게 끝날 일이지만 조금 복잡하지만 대수막대로 인수분해를 해석해 보기로 하자. 수학 수업에서 이렇게 설명하면 이런 것이 시험에 나오냐고 묻는 아이들이 있다. 당연히 이런 것도 시험에 나온다고 대답한다. 시험에 나오지 않는다고 하더라고 이렇게 분석하는 일은 매우 중요하다. 고등학교에 진학해서도 수학을 잘하고 싶다면 중학교 때부터 수학 공부를 할 때 공식을 암기하는 것에 그치지 말고 공식을 이해하고 창의적으로 활용하는 것에 흥미를 가져야 한다.

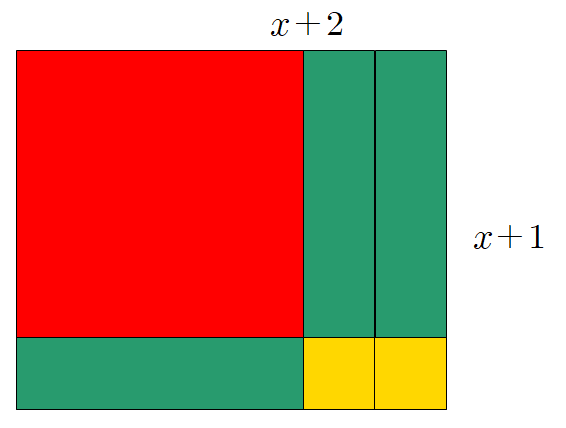
위 그림으로 아래 인수분해를 간단하게 설명할 수 있다.

$$x^2 +3x+2=(x+1)(x+2)$$

노란색 직사각형이 넓이가 $ab$이라고 하면 위 그림은 아래 공식을 뜻하게 된다.

$$\begin{split}x^2 +(a+b)x+ab&=x^2+ax+bx+ab\\&=x(x+a)+b(x+a)\\&=(x+a)(x+b)\end{split}\tag{1}$$

결국 중학교 인수분해는 사각형 막대를 재배열하여 직사각형을 만드는 퍼즐과 같다.

$$x^2+5x+2$$

먼저 정사각형을 직사각형으로 배열하는 방법을 찾아보면 $1\times 2$나 $2\times 1$ 밖에 없다. 

아래 그림과 같이 정사각형을 같은 꼴로 배열하면 직사각형이 4개만 필요하게 된다. 

따라서 아래와 같이 다른 꼴($1\times 2$과 $2\times 1$)로 배열하여 다음과 같이 인수분해함을 알 수 있다.

$$x^2+5x+2=(2x+1)(x+2)$$

위 (1)과 마찬가지로 빨간 부분과 노란 부분의 넓이가 각각 $acx^2$, $bd$라고 하자.

$$\begin{split}acx^2 +(ad+bc)x+bd&=acx^2+adx+bcx+bd\\&=ax(cx+d)+b(cx+d)\\&=(ax+b)(cx+d)\end{split}\tag{2}$$