이집트 분수 이야기

고대 이집트인도 분수를 사용했다. 그런데 오늘날 우리와 달리 주로 분자가 1인 단위분수를 사용했다고 한다. (예외 2/3는 사용) 숫자를 나타내는 상형문자 위에 눈을 그려서 역수를 표시했기 때문에 단위분수를 쓰게 되었을 것이라고 추측한다.

이집트인이 사용한 분수 이야기를 조금 더 해보자. 빵 5개를 8명이 나누어 가진다고 하자. 우리는 간단하게 5/8씩 나누면 된다고 생각하지만 실제로 나눌 때 5/8로 나누기는 생각보다 복잡하다. 모든 빵을 8등분 하고 5개씩 나누어 가지는 일은 어리석은 일이다.

이집트인들은 먼저 빵 4개를 1/2씩 나누어 가지고 나머지 1개만 8개로 나누어 하나씩 가진다고 생각했다. 어떤 때는 이집트인처럼 단위분수로 하는 계산이 더 간편하다.

$$\frac{5}{8}=\frac{1}{2}+\frac{1}{8}$$

분수와 관련된 옛날이야기 몇몇을 찾아 적는다.

이집트의 부적 호루스의 눈

호루스의 눈(우제트, Wedjat, Wadjet, Udjat, Udjet)은 고대 이집트의 신격화된 파라오의 왕권을 보호하는 상징이다. 태양의 눈, 라의 눈 또는 달의 눈이라고도 불린다. 호루스의 눈은 건강과 총체적인 인식과 이해를 상징한다. 오른쪽 눈은 라의 눈으로 태양을 상징하고 왼쪽 눈은 토트의 눈으로 달을 상징한다. 파라오와 왕권을 지켜주는 상징 외에, 이집트 장례의식에서 미라가 착용하는 귀금속으로 사용되었으며, 근동지역에서는 뱃머리에 그려 넣는 용도로 사용되었다. 위키백과 

호루스의 눈이 들어간 부적

1911년 이집트학자 게오르그 묄러(Georg Möller)는 '호루스의 눈'을 나타내는 상형 문자가 분수를 나타내는 기호로 쓰였다고 가정했다. 눈 안쪽 모서리는 1/2, 눈동자는 1/4, 눈썹은 1/8, 바깥쪽 모서리는 1/16, 컬링 라인은 1/32, 볼 마크는 1/64로 설정했다. 위키백과

 

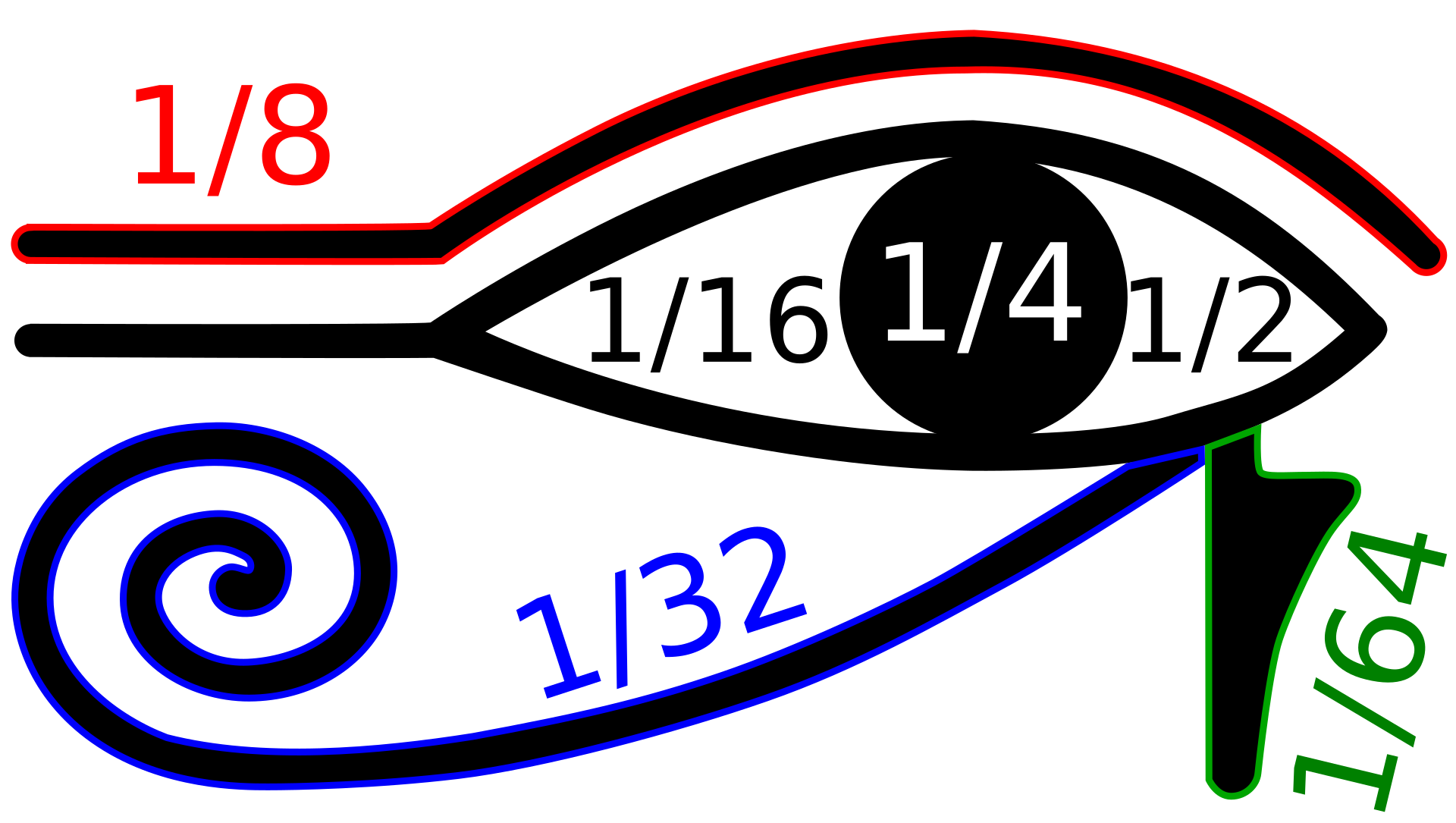
$$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}=\frac{63}{64}$$

전설에 따르면 세트 신이 빼앗어 버린 1/64을 토르 신이 되찾아 1을 만들어 주었다고 한다. 고대 이집트 신화에 등장하는 분수 이야기라니 흥미롭지 아니한가?

아랍의 낙타 문제

아랍에 전해져 내려온다는 유명한 문제도 있다.

어느 마을에 부자가 낙타 17마리를 유산으로 남기며 아들 셋에게 큰 아들은 1/2, 둘째는 1/3, 막내는 1/9을 가지라는 유언을 남겼다. 어떻게 나누면 되는가?

워낙 유명한 이야기라 다들 한 번은 풀어 보았을 문제다. 17은 소수라 2, 3, 9로 나누어 떨어지지 않는다. 어찌할 바를 모르던 삼 형제에게 때마침 지나가던 현자가 낙타 한 마리를 건네며 나눠 가지게 했다. 맏이는 9마리, 둘째는 6마리, 막내는 2마리를 가지고 1마리는 다시 현자가 가지고 가면 된다.

$$\frac{1}{2}+\frac{1}{3}+\frac{1}{9}+\frac{1}{18}=1$$

린드 파피루스 문제

이집트 수학 문제를 적은 린드 파피루스에 단위분수로 분해하는 문제가 있다. 예를 들면 빵 9개를 10명이 나누어 가지는 방법과 같은 문제가 있다.

$$\frac{9}{10}=\frac{2}{3}+\frac{1}{5}+\frac{1}{30}$$

1. 빵 7개를 각각 3등분하여 2개씩 나누어 가진다. 1/3조각이 남는다.

2. 빵 2개를 각각 5등분하여 1개씩 나누어 가진다.

3. 1에서 남은 1/3조각을 10등분하여 하나씩 나누어 가진다.

린드 파피루스에 나오는 문제를 간단하게 줄이면 다음과 같다.

단위분수들의 합이 1보다 작을 때 적당한 단위분수를 몇 개 더해서 1이 되는 분수를 찾아라. 예를 들면

$$\frac{1}{2}+\frac{1}{3}<1$$

일 때

$$\frac{1}{2}+\frac{1}{3}+\frac{1}{x}+\frac{1}{y}=1\tag{1}$$

이 되는 분수 $\displaystyle{\frac{1}{x},\frac{1}{y}}$을 찾아라.

별로 주목을 받지 못하던 문제를 1202년 수학자 피보나치가 풀면서 중요한 문제가 되었다. (1)과 같이 정수인 해를 구하는 부정 방정식을 디오판토스 방정식(Diophantine equation)이라 한다.

피보나치는 모든 분수는 서로 다른 단위분수의 합으로 나타낼 수 있음을 증명하였다.

아래와 같은 항등식으로 단위분수의 무한 사슬을 만들 수 있다.

$$\frac{1}{a}=\frac{1}{a+1}+\frac{1}{a(a+1)}$$

 

피보나치 알고리즘

피보나치는 주어진 분수를 다음과 같은 알고리즘으로 단위분수의 합으로 나타냈다. 영어로 탐욕 알고리즘$_{Greedy Algorithm}$으로 부르는데 컴퓨터 프로그래밍 배울 때 많이 쓰인다.

1단계. 주어진 분수보다 작으면서 가장 가까운 단위분수를 찾는다.

2단계. 주어진 분수에서 1에서 찾은 단위분수를 빼고 반복한다.

5/21에 적용해 보자.

1. 5/21에 가장 가까운 단위분수 1/5를 찾는다. $$\frac{1}{5}<\frac{5}{21}<\frac{1}{4}$$

2. 1/5를 빼서 4/105를 얻는다. $$\frac{5}{21}-\frac{1}{5}=\frac{4}{105}$$

3. 2에서 얻은 4/105에 가까운 단위분수 1/27을 찾는다. $$\frac{1}{27}<\frac{4}{105}<\frac{1}{26}$$

4. 1/27을 빼면 단위분수가 나오므로 답을 찾았다. $$\frac{5}{21}-\frac{1}{5}-\frac{1}{27}=\frac{1}{945}$$

$$\therefore\;\;\frac{5}{21}=\frac{1}{5}+\frac{1}{27}+\frac{1}{945}$$

남은 이야기

에르도스(Paul Erdős)와 스트라우스(E. G. Straus)는 모든 자연수 $n>2$에 대하여 아래와 같은 방정식이 반드시 정수해 $a,b,c$를 가진다고 추측하였다.

$$\frac{4}{n}=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$$

이와 비슷하게 시어핀스키(Sierpiński )는 1956년 아래와 같은 방정식을 해결할 수 있다고 예측했는데 구이(Guy)가  1994년에 해결하였다.

$$\frac{5}{n}=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$$

 

---

참고

 

경문사

 

Eye of Horus - Wikipedia

 

Get updates, career advice, and job market news on the FutureLearn Blog

 

Wolfram MathWorld: The Web's Most Extensive Mathematics Resource