작도가능한 수
수학이야기 2023. 10. 27. 16:35기하에서 작도는 컴퍼스와 눈금이 없는 자(compass and straightedge)로 도형을 만드는 일이다. 유클리드 '원론'은 대표적인 작도 교과서이다. 중학교 1학년에서 잠깐 다루고 말지만 깊이 파고들면 참 재밌는 분야이다. 작도와 관련하여 대수에서도 '작도가능한 수'가 나온다.
작도가능한 수(constructible number)
전자는 작도가능한 수를 기학적으로 정의한 것이고 후자는 대수적으로 정의했다고 말할 수 있다.
일찍이 유클리드는 다섯 가지 공준을 밝히며 그 유명한 원론을 시작한다.
원론(Euclid's Elements) 1권
우연히 알게 된 'Euclid's Elements'에서 옮겨다 놓고 하나씩 우리말로 옮겨볼까 생각하고 있다. 연결된 사이트에서 그림을 보기 위해서는 자바(java) 프로그램 구성에서 보안 설정을 바꿔 주어야 한다
suhak.tistory.com
공준 1 임의의 점에서 임의의 점으로 직선을 그을 수 있다.
공준 2 선분을 이어서 직선을 만들 수 있다.
공준 3 임의의 중심과 반지름을 가진 원을 그릴 수 있다.
위에 있는 공준 1과 2는 눈금이 없는 자로 3은 컴퍼스로 할 수 있는 일을 밝힌 것이다. 특히 공준 3은 원을 그리기 위해 반지름을 나타내는 선분을 움직여도 선분 길이가 달라지지 않도록 공간상의 거리가 정의되었음을 뜻한다. 세상 모든 것이 그러하듯 측정하려면 반드시 단위가 필요하다. 주어진 단위 길이가 있을 때 작도가능한 길이를 찾아보자.
예를 들면 아래와 같은 그림에서 $\sqrt {2}$가 작도가능함을 알 수 있다.
자연수와 정수
단위 길이를 가진 선분을 연장하고 컴퍼스로 단위 길이만큼을 늘어난 점을 찾으면 된다. 단위 길이를 1이라고 하면 1+1=2가 작도가능하므로 모든 자연수는 모두 작도가능하다.

참고: 페아노 공리
음수는 방향만 정하면 되므로 자연수가 작도가능하면 0과 음의 정수를 포함한 모든 정수도 작도가능하다.
이등분한 수
이것은 원론에 가장 먼저 등장하는 작도이다.

이어서 주어진 길이를 가지는 선분을 작도하는 방법이 나온다. 나중에는 주어진 각과 같은 크기를 가지는 각을 작도하는 방법도 등장한다. 길이와 각의 크기를 옮길 수 있으므로 합동인 삼각형은 작도가능하다. 삼각형을 작도하는 방법을 활용하면 작도가능한 수의 곱셈과 나눗셈으로 나타낼 수 있는 수를 작도할 수 있다.
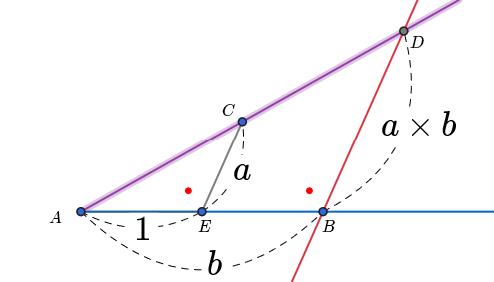
곱셈
나눗셈

제곱근
산술평균과 기하평균을 작도하면서 작도가능한 수의 제곱근도 작도할 수 있다.

대수적인 성질
작도가능한 수의 집합을 $\mathbb{F}$라고 하자. 집합 $\mathbb{F}$는 모든 유리수를 포함하고 유리수의 제곱근까지 포함한 집합이다.
$\mathbb{F}$에서 덧셈과 곱셈이 잘 정의되고, 닫혀 있으며 0을 제외한 모든 원소의 역원까지 존재한다. 작도가능한 수의 집합 $\mathbb{F}$는 대수적으로 체(field)를 이룬다.
작도할 수 없는 세 가지 문제
정육면체 부피를 2배로 만들기
고대 그리스 신화에 바탕을 둔 델리안(delian) 문제라고도 부른다.
고대 그리스 도시 델로스에 전염병이 돌아서 혼란에 빠졌을 때 시민들은 아폴론 신전에 물어서 정육면체인 제단을 부피가 딱 2배인 제단으로 만들면 전염병이 사라진다는 신탁을 받았다.
작도하라는 제약이 있다면 이 신탁에 등장하는 수는 작도할 수 없다.
방정식 $x^3=2$의 근인 $x=\sqrt [3]{2}$은 작도불가능한 수이다.
임의의 각을 3등분하기
직각과 같이 특별한 각을 3등분하는 것은 가능하다. 하지만 임의의 각을 3등분하는 작도는 불가능하다. 하지만 눈금이 있는 자를 활용하면 가능하다.
원과 넓이가 같은 정사각형 만들기
원적 문제로 알려진 문제다. 수많은 수학자를 절망하게 만든 가장 유명한 문제가 아닐까 싶다. 하지만 이 문제에 도전하면서 얻어낸 성과가 아주 많다.
방정식 $x^2=\pi$의 근인 $\sqrt{\pi}$는 작도불가능하다.











