미분과 극한

미분은 극한에서 시작한다. 뉴턴은 평균 속도에서 순간 속도로 라이프니츠는 자르는 선(secant line)의 기울기에서 접선 기울기로 나아갔다. 바깥고리 << 위키백과 미분 >>

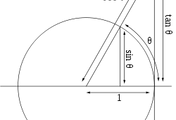
함수 $y=f(x)$에서 $x$가 $x=a$에서 $x=a+\Delta x$까지 변할 때, $y$의 변화량 $\Delta y$는 $f(a+ \Delta x)-f(a)$이다.

이때, 할선(secant line)의 기울기 $m$은 아래와 같다.

$$m= \frac{\Delta y}{\Delta x} =\frac{f(a+ \Delta x)-f(a)}{\Delta x}$$

위 그림에서 점 $Q$가 점 $P$로 한 없이 가까워 진다고 하면 접선(tangent line)과 한 없이 가까워질 것이다. 따라서 할선의 기울기의 극한값은 접선의 기울기일 것이다. 이때 접선의 기울기를 미분계수로 정의한다.

함수 $y=f(x)$에서 $x=a$일 때, 미분계수(derivative of f at $x=a$) $f^{\prime} (a)$를 아래와 같이 정의한다.

$$f ^{\prime}(a) =\lim_{\Delta x\rightarrow 0}\frac{f(a+ \Delta x)-f(a)}{\Delta x}$$

$a$와 미분계수 $f ' (a)$ 사이 함수 다시 말하면 함수 $f^{\prime}: x \rightarrow f^{\prime}(x)$를 함수 $f(x)$의 도함수(derivative of $f$)라고 한다.

$$f  ' (x) =\lim_{h \rightarrow 0}\frac{f(x+ h)-f(x)}{h}$$

기호로 $ \displaystyle{f^{\prime}(x) , \;y ^{\prime} ,\; \frac{dy}{dx}   ,\; \frac{d}{dx}f(x)}$로 적는다. 여러 가지 표현이 있는 까닭은 라이프니츠, 라그랑제, 뉴튼, 오일러가 각기 다른 표현을 썼기 때문이다.

도함수(derivative of $f$)를 구하는 것을 미분한다(diffentiation)고 하고 그 계산법을 미분법으로 부른다. ($dy$를 $dx$로 나눈 것처럼 보이지만 조금 다른 뜻을 품고 있는 기호이다. 읽을 때는 그냥 'dy dx'로 읽는다.)

시간 $t$에 따라 정해지는 위치를 나타내는 함수 $x=x(t)$를 생각한다면 자르는 선의 기울기는 평균 속도이고 극한값은 순간 속도이다. 

$$\frac{\Delta x}{\Delta t}=\frac{x(a+ \Delta t)-x(a)}{\Delta t}$$

$$v(a)=x^{\prime}(a)=\lim_{\Delta t\rightarrow 0}\frac{\Delta x}{\Delta t}=\lim_{\Delta t\rightarrow 0}\frac{x(a+ \Delta t)-x(a)}{\Delta t}$$

평균변화율과 순간변화율로 부르는 것도 같은 것을 뜻한다.

할선(secant line)

접선(tangent line)

 

 

미분

 

 

미분으로 무엇을 알 수 있을까? 뉴턴은 순간 속도를 구했고 라이프니츠는 접선의 기울기를 구했다.

오른쪽 그림은 함수 $f(x)=x\sin x^2 +1$의 그래프와 접선을 보여주고 있다. 녹색으로 보이는 접선은 기울기가 양이고 검은 것은 기울기가 $0$ 붉은 것은 기울기가 음이다.

미분계수가 양이냐 음이냐에 따라 함숫값이 증가하는가 감소하는가를 알 수 있다. 증감을 알면 함수가 언제 극값을 가지는가도 알 수 있다. 미분가능한 함수라면 미분계수가 $0$이고 부호가 바뀌는 점에서 극값을 가진다.

정리: 함수 $f(x)$가 $x=a$에서 미분가능하고 극값을 가지면 $f^{\prime}(a)=0$이다.

복잡해서 그래프를 그리기 어려운 함수는 도함수를 이용하여 증감을 조사하여 극값을 찾아 개형을 그릴 수 있다.

참고: 대학에서 배우는 미적분에서는 라이프니츠가 쓴 표현에서 $dy$, $dx$를 각각 변수로 생각하여 $$dy=f^{\prime}(x)dx$$로 표현할 수 있다. 

각각 differential dy, differential dx로 읽는다.