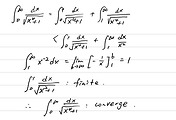Exercises 8.5

오타가 많아서 새로 쳤다. 31

$$\int\frac{2\theta^3 +5\theta^2 +8\theta+4}{(\theta^2 +2\theta+2)^2}d\theta$$

$$=\int\frac{(\theta^2 +2\theta^2 +2)(2\theta+2)-\theta^2}{(\theta^2 +2\theta+2)^2}d\theta$$

$$=\int\frac{2\theta+2}{\theta^2 +2\theta+2}d\theta-\int\frac{\theta^2}{(\theta^2 +2\theta+2)^2}d\theta$$

$$=\ln(\theta^2 +2\theta+2)-\int\frac{\theta^2 +2\theta+2-(2\theta+2)}{(\theta^2 +2\theta+2)^2}d\theta$$

$$=\ln(\theta^2 +2\theta+2)-\int\frac{1}{\theta^2 +2\theta+2}d\theta+\int\frac{2\theta+2}{(\theta^2 +2\theta+2)^2}d\theta$$

$$=\ln(\theta^2 +2\theta+2)-\tan^{-1}(\theta+1)-\frac{1}{\theta^2 +2\theta+2}+C$$