케플러 행성 운동 법칙에 관한 공부
수학이야기/Calculus 2019. 10. 22. 16:42원운동과 같은 운동은 동경과 편각에 따라 결정되는 것이 많아서 극좌표나 구면 좌표를 써야 편하다. 실제로 과학 공부엔 극좌표가 훨씬 유용하다. 그럼 이제 직교 좌표계가 아닌 다른 좌표계에서 운동은 어떻게 표현될까 알아보자.
극좌표
극좌표 평면에 있는 점 $P(r,\theta)$가 주어진 곡선을 따라 운동할 때, 위치, 속도, 가속도를 나타내는 방법을 찾아보자. 극좌표에서는 직교좌표에서 쓰는 $\mathbf {i},\mathbf {j}$ 기본단위 벡터 대신에 아래에 있는 단위 벡터 $\mathbf {u}_r,\mathbf {u}_{\theta}$를 써서 나타낸다. 이때 두 벡터에 곱해지는 스칼라를 성분으로 생각하면 쉽게 이해할 수 있다.
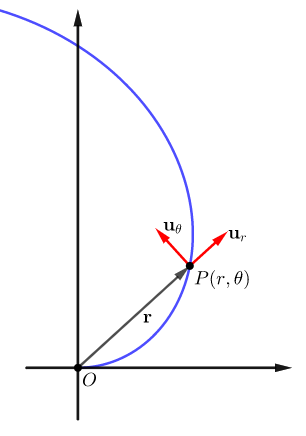
$$\begin {equation}\mathbf {u}_r=(\cos\theta)\mathbf {i}+(\sin \theta)\mathbf{j},\;\;\;\mathbf{u}_{\theta}=-(\sin\theta)\mathbf{i}+(\cos \theta)\mathbf{j}\end{equation}$$
그림과 같이 벡터 $\mathbf{u}_r$은 위치 벡터 $\overrightarrow{OP}$와 같은 방향이므로 $\mathbf{r}=r\mathbf{u}_r$이다. 벡터 $\mathbf{u}_{\theta}$는 벡터 $\mathbf{u}_r$와 수직이고 $\theta>0$인 방향이다.
$$\begin{split}\frac{d \mathbf{u}_r}{d \theta}&=-(\sin\theta)\mathbf{i}+(\cos\theta)\mathbf{j}=\mathbf{u}_{\theta}\\ \frac{d \mathbf{u}_{\theta}}{d \theta}&=-(\cos\theta)\mathbf{i}-(\sin\theta)\mathbf{j}=\mathbf{u}_r\end{split}$$
이제 시각 $t$에 대한 미분을 해보자. 여기서 시각 $t$에 대한 미분은 $dx/dt=\dot x$와 같이 점을 찍는 뉴턴 표기법으로 쓰기로 하자.
$$\dot {\mathbf{u}}_r=\frac{d \mathbf{u}_r}{d\theta}\dot{\theta}=\dot{\theta}\mathbf{u}_{\theta},\quad \dot {\mathbf{u}}_{\theta}=\frac{d \mathbf{u}_{\theta}}{d\theta}\dot{\theta}=-\dot{\theta}\mathbf{u}_r$$
그러므로 속도와 가속도를 두 벡터 $\mathbf{u}_r,\mathbf{u}_{\theta}$로 나타낼 수 있다.
$$\mathbf{v}=\dot{\mathbf{r}}=\frac{d}{dt}(r\mathbf{u}_r)=\dot r\mathbf{u}_r+r\dot{\mathbf{u}}_r =\dot r\mathbf{u}_r+r\dot{\theta}\mathbf{u}_{\theta}$$
$$\begin{split}\mathbf{a} = \dot {\mathbf{v}}&= (\ddot{r} \mathbf{u}_r + \dot{ r }\dot{\mathbf{u}}_r )+(\dot{ r }\dot{\theta} \mathbf{u}_{\theta}+r \ddot{\theta} \mathbf{u}_{\theta}+r\dot{\theta} \dot{\mathbf{u}}_{\theta})\\&= \ddot{r} \mathbf{u}_r + \dot{ r }\dot{\theta}\mathbf{u}_{\theta} +\dot{ r }\dot{\theta} \mathbf{u}_{\theta}+r \ddot{\theta} \mathbf{u}_{\theta}+r\dot{\theta}( -\dot{\theta}\mathbf{u}_r)\\ & = (\ddot {r}-r {\dot{\theta}}^2) \mathbf{u}_r + (r\ddot{\theta} +2\dot{r}\dot{\theta}) \mathbf{u}_{\theta}\end{split}\tag{1}$$

원기둥 좌표
위에서 계산한 바를 확장하면 아래 그림과 같은 원기둥 좌표로 표현할 수 있다.
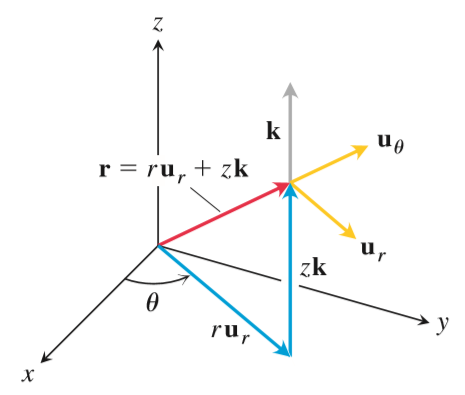
그림에서 $z\not=0$이면 $|\mathbf{r}|\not=r$이고 $|\mathbf{r}|=\sqrt{r^2+z^2}$이다. 세 벡터 $\mathbf{u}_r, \mathbf{u}_{\theta}, \mathbf{k}$는 오른손 법칙에 따라 방향을 정한다
$$\mathbf{u}_r \times \mathbf{u}_{\theta} = \mathbf{k}, \quad \mathbf{u}_{\theta} \times \mathbf{k}=\mathbf{u}_r, \quad \mathbf{k}\times \mathbf{u}_r = \mathbf{u}_{\theta}$$
위치 벡터 $\mathbf{r}=r\mathbf{u}_r+z\mathbf{k}$
속도 $\mathbf{v}=\dot r\mathbf{u}_r+r\dot{\theta}\mathbf{u}_{\theta}+\dot{z}\mathbf{k}$
가속도 $\mathbf{a} =\dot {\mathbf{v}}= (\ddot{r} \mathbf{u}_r + \dot{ r }\dot{\mathbf{u}}_r )+(\dot{ r }\dot{\theta} \mathbf{u}_{\theta}+r \ddot{\theta} \mathbf{u}_{\theta}+r\dot{\theta} \mathbf{u}_{\theta})+\ddot{z}\mathbf{k}$
행성 운동
중력에 관한 뉴턴 법칙은 아래와 같다. $\mathbf{r}$은 질량이 $M$인 태양의 중심으로부터 질량이 $m$인 행성의 중심까지 반지름 벡터라면 $F$는 태양과 행성이 서로에게 미치는 중력이다. $G=6.6738\times10^{-11}Nm^2 kg^{-2}$는 만유인력 상수다.
$$\mathbf{F}=- \frac{GmM}{|\mathbf{r}|^2} \frac{\mathbf{r}}{|\mathbf{r}|}$$

뉴턴 운동 제2법칙에 따르면 $\mathbf{F}=m\mathbf{a}=m\ddot{\mathbf{r}}$이다. 따라서
$$\begin{split}m\ddot{\mathbf{r}}&=- \frac{GmM}{|\mathbf{r}|^2} \frac{\mathbf{r}}{|\mathbf{r}|}\\ \ddot{\mathbf{r}}&=- \frac{GM}{|\mathbf{r}|^2} \frac{\mathbf{r}}{|\mathbf{r}|}\end{split}\tag{2}$$
행성은 항상 태양의 중심 방향으로 가속도가 생긴다. 가속도 벡터 $\ddot{\mathbf{r}}$은 벡터 $\mathbf{r}$의 실수배이므로 외적은 영벡터가 된다.
$$\mathbf{r}\times\ddot{\mathbf{r}}=\mathbf{0}$$
$$\frac{d}{dt}(\mathbf{r}\times\dot{\mathbf{r}})=\underbrace{\dot{\mathbf{r}}\times \dot{\mathbf{r}}}_{0}+\mathbf{r}\times\ddot{\mathbf{r}}=\mathbf{0}$$
$$\mathbf{r}\times\dot{\mathbf{r}}=\mathbf{C}$$
$\mathbf{C}$는 크기와 방향이 일정한 상수 벡터이다. 위에 있는 식은 두 벡터 $\mathbf{r},\dot{\mathbf{r}}$가 항상 $\mathbf{C}$가 법선벡터인 평면에 놓여 있음을 뜻한다. 따라서 행성은 항상 태양의 중심을 품은 고정된 평면에서 움직인다.
케플러 행성 운동 법칙
이제 행성이 운동하는 궤도는 어떤 곡선인가 찾아보자. (1)식에 (2)에서 구한 가속도를 대입한다.
$$(\ddot {r}-r {\dot{\theta}}^2) \mathbf{u}_r + (r\ddot{\theta} +2\dot{r}\dot{\theta}) \mathbf{u}_{\theta}=- \frac{GM}{|\mathbf{r}|^2} \frac{r\mathbf{u}_r}{|\mathbf{r}|}\tag{3}$$
$\mathbf{u}_r, \mathbf{u}_{\theta}$에 대한 성분만 따로 정리하면 아래와 같다. 여기서 $|\mathbf{r}|=r$이다.
$$\begin{split} \ddot {r}-r {\dot{\theta}}^2 &= - \frac{GM}{r^2} \\ r\ddot{\theta} +2 \dot{r} \dot{\theta}&=0 \end{split}\tag{4}$$
무서운 미분방정식이 둘이나 나왔다. 다행스럽게도 아주 어렵지는 않아서 미분방정식을 따로 공부하지 않았어도 과정을 이해할 수는 있다. 먼저 두 번째 식을 보자.
$$r\ddot{\theta} +2\dot{r}\dot{\theta}=0$$
$$r^2\ddot{\theta} +2r\dot{r}\dot{\theta}=0$$
$$\frac{d}{dt}(r^2\dot{\theta})=0$$
$$r^2\dot{\theta}=\mu\tag{5}$$
$\mu$는 시간과 관계없이 일정한 상수이다. 따라서 행성이 $\theta_0$부터 $\theta$까지 움직일 때 넓이를 $S$라고 하면 아래와 같다.
$\displaystyle{S(\theta)=\int_{\theta_0}^{\theta} \frac{1}{2}r^2 d{\theta}}$이므로 $\displaystyle{\frac{dS}{d\theta}= \frac{1}{2}r^2}$
$$\frac{dS}{dt}=\frac{dS}{d\theta}\frac{d\theta}{dt}=\frac{1}{2}r^2 \dot{\theta}=\frac{1}{2}\mu$$
$\blacksquare$
이것은 시간에 대한 넓이의 변화율이 일정함을 보여준다. 같은 시간에 동경이 쓸고 지나는 부분은 넓이가 같다는 케플러 행성 운동 제2 법칙이 증명되었다.
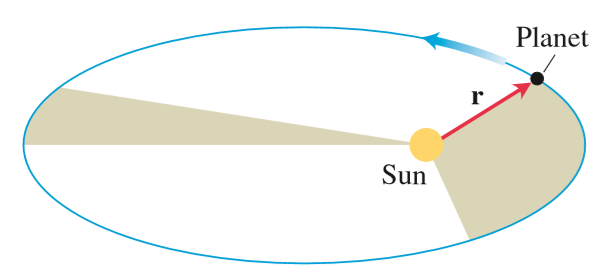
위에서 구한 결과 (5)를 정리한 $\displaystyle{\dot{\theta}=\frac{\mu}{r^2}}$를 첫 번째 식에 넣어보자.
$$\ddot {r}-r \bigg(\frac{\mu}{r^2}\bigg)^2= - \frac{GM}{r^2}$$
$$r^2\ddot {r}-\frac{{\mu}^2}{r}= - GM\tag{6}$$
많이 간단해졌다. 극좌표로 표현된 해를 얻어야 하므로 $\ddot{r}$를 $\theta$에 대한 미분으로 바꿔보자.
$$\dot r = \frac {d r} {d t} = \frac {d r} {d \theta} \frac { d \theta} { d t} = \frac { d r} { d \theta} \dot {\theta} = \frac {d r} {d \theta} \frac {\mu} {r^2}$$
$$\ddot r = \frac {d} {d t} \left( \dot r \right) = \frac {\text d} {\text d \theta} \left( \dot r \right) \frac {d \theta} {dt} = \dot \theta \frac {d} {d \theta} \left( \frac {d r} {d \theta} \frac {\mu} {r^2} \right) =\frac{\mu^2}{r^2} \frac {d} {d \theta} \left( \frac {1} {r^2} \frac {d r} {d \theta} \right) \tag{7}$$
(7)을 위에 있는 식 (6)에 대입하여 정리하면 아래와 같다.
$$\mu^2 \frac {\text d} {\text d \theta} \left( \frac {1} {r^2} \frac {\text d r} {\text d \theta} \right) - \frac {\mu^2}{r} = - {GM} $$
정리한 식을 $\mu^2$으로 나누어 정리하자.
$$\frac {\text d} {\text d \theta} \left( \frac 1 {r^2} \frac {\text d r} {\text d \theta} \right) - \frac {1}{r} = - \frac {GM} {\mu^2}\tag{8}$$
이제 거의 마무리 단계다.
$\displaystyle{\lambda=\frac{1}{r}}$로 치환하고 양변을 $\theta$에 대하여 미분하자.
$$\frac {d \lambda} {d \theta} = -\frac {1} {r^2} \frac {\text d r} {d \theta}\tag{9}$$
(9)를 (8)에 대입하여 식을 다시 정리하자.
$$- \frac {\text d^2 \lambda} {\text d \theta^2} - \lambda = - \frac {GM} {\mu^2}$$
$$- \frac {\text d^2 \lambda} {\text d \theta^2} = \lambda -\frac {GM} {\mu^2}\tag{10}$$
$GM/\mu^2$은 상수이므로 미분방정식에서 큰 자리를 차지하지 못한다. 아래와 같이 써도 된다.
$$- \frac {d^2} {d \theta^2}\bigg( \lambda -\frac {GM} {\mu^2}\bigg) = \lambda -\frac {GM} {\mu^2}$$
해석하자면 함수 $\displaystyle{\lambda-\frac{GM}{\mu^2}}$를 $\theta$에 대한 이계도함수가 부호만 바뀌었다. 그러므로 $y^{\prime\prime}=-y$와 같은 꼴이다. 이런 꼴을 비동차 선형 미분방정식으로 분류한다. 조화 진동자 풀이에 나오는 미분방정식과 같은 꼴이다.
비동차 선형 미분방정식을 풀이하는 법은 다른 글에서 설명하기로 하고 여기서는 이계도함수가 원래 함수와 같아지거나 부호만 바뀌는 함수는 지수함수와 삼각함수가 있다는 사실만 기억하자. 위와 같은 꼴인 미분방정식은 $\cos \theta$를 해로 가진다.
$$\lambda -\frac {GM} {\mu^2}=A\cos\theta$$
$$\frac{1}{r} -\frac {GM} {\mu^2}=A\cos\theta$$
$$r= \frac{1}{\frac {GM} {\mu^2}+A\cos\theta}= \frac{\frac {\mu^2}{GM}}{1+\frac {\mu^2}{GM}A\cos\theta}$$
$\displaystyle{\frac {\mu^2}{GM}=l, \frac {\mu^2}{GM}A=e}$라고 하면 아래와 같이 정리되는데 이것은 이심률이 $e$인 타원의 극방정식이다.
$$r= \frac{l}{1+ e\cos\theta}$$
더 정확하게 표현해보자. 태양에 가장 가까울 때 태양과 행성을 잇는 직선을 시초선으로 잡자. 이때 $t=0$라고 하고 거리는 $r_0$, 속도는 $v_0$라 하자.
위에서 구한 속도를 다시 보자.
$$\mathbf{v}=\dot{\mathbf{r}}=\dot r\mathbf{u}_r+r\dot{\theta}\mathbf{u}_{\theta}$$
속도는 축과 수직인 방향이므로 $\dot{r}=0$이고 $v_0=r_0 \dot{\theta}$이다.
$$\begin{split}\mathbf{C} &= \mathbf{r} \times \dot{\mathbf{r}} = \mathbf{r} \times \mathbf{v} \\ &= r\mathbf{u}_r \times (\dot{r} \mathbf{u}_r + r \dot{\theta} \mathbf{u}_{\theta} ) \\ &= r\dot{r} \underbrace{ (\mathbf{u}_r \times \mathbf{u}_r)}_{\mathbf{0}} + r(r\dot{\theta}) \underbrace{(\mathbf{u}_r \times \mathbf{u}_{\theta})}_{\mathbf{k}} \\ &= r(r\dot{\theta}) \mathbf{k} \end{split}$$
다시 정리하면 아래와 같이 상수 벡터가 정해진다.
$$\mathbf{C}=[r(r\dot{\theta})]_{t=0} \mathbf{k} = r_0 v_0 \mathbf{k}$$
$\displaystyle{\mu=r_0 v_0,\quad A=\frac{1}{r_0}-\frac{GM}{r_0^2 v_0^2}}$이므로 이심률은 $$\displaystyle{e=\frac{r_0 v_0^2}{GM}-1}\tag{11}$$이다.
$$\displaystyle{r= \frac{(1+e)r_0}{1+ e\cos\theta}}\tag{12}$$
$\blacksquare$
행성은 타원 궤도를 따라 운동한다는 케플러 행성 운동 제1 법칙을 증명하였다.
마지막으로 케플러 행성 운동 제3 법칙은 아래와 같다.
공전주기를 $T$라 하고 장축 길이를 $2a$라고 하면 모든 행성은 $T^2/a^3$의 값이 일정하다.
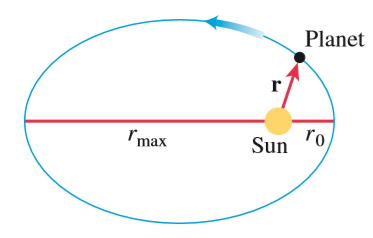
타원의 넓이는 아래와 같이 계산할 수 있다.
$$A=\int_{0}^{T}dA=\int_{0}^{T}\frac{1}{2}r_0 v_0 dt= \frac{1}{2}Tr_0 v_0$$
단축의 길이가 $2b$인 타원은 넓이가 $\pi ab$이므로 아래가 성립한다.
$$T=\frac{2\pi ab}{r_0 v_0}=\frac{2\pi a^2}{r_0v_0}\sqrt{1-e^2}\quad\quad\because b=a\sqrt{1-e^2}\tag{13}$$
(12)에 있는 식에 $\theta=\pi$를 대입하면 아래와 같다.
$$r_{max}= r_0 \frac{1+e}{1-e}$$
$$2a=r_0 +r_{max}=\frac{2r_0}{1-e}$$
$$\therefore\quad 1-e=\frac{r_0}{a}\tag{14}$$
$$1+e=\frac{r_0 v_0^2}{GM}\tag{15}$$
(13)의 양변을 제곱하고 위에 있는 식 (14), (15)을 대입하자.
$$\begin{split}T^2&= \frac{4\pi^2 a^4}{r_0^2 v_0^2}(1-e)(1+e) \\& = \frac{4\pi^2 a^4}{r_0^2 v_0^2} \times \frac{r_0}{a} \times \frac{r_0 v_0^2}{GM} \\& = \frac{4\pi^2 a^3}{GM}\end{split}$$
$$\frac{T^2}{a^3}=\frac{4 \pi^2}{GM}$$
$\blacksquare$
미분방정식을 쓰지 않고 궤도 찾기
위에 있는 (2)에서 시작하자.
$$\ddot{\mathbf{r}}=- \frac{GM}{|\mathbf{r}|^2} \frac{\mathbf{r}}{|\mathbf{r}|}\tag{2}$$
먼저 위치벡터와 방향이 같은 단위벡터를 $\mathbf{u}$라고 하면 $\mathbf{r}=r\mathbf{u}$이다. ($|\mathbf{r}|=r$)
위에 있는 식에 대입해 보자.
$$\ddot{\mathbf{r}}=- \frac{GM}{|\mathbf{r}|^2} \frac{r\mathbf{u}}{|\mathbf{r}|}= - \frac{GM}{r^2} \mathbf{u}$$
$GM=\alpha$라고 치환하자. 두 벡터를 다시 정리해 보자.
$$\mathbf{r}=r\mathbf{u}\quad\quad \ddot{\mathbf{r}}= - \frac{\alpha}{r^2} \mathbf{u}$$
두 벡터는 평행이므로 외적은 $\mathbf{r} \times \ddot{\mathbf{r}}=0$이다.
$$\displaystyle{\frac{d}{dt}(\mathbf{r} \times \dot{\mathbf{r}})=\underbrace{\dot{\mathbf{r}}\times \dot{\mathbf{r}}}_{0}+\mathbf{r}\times\ddot{\mathbf{r}}=\mathbf{r} \times \ddot{\mathbf{r}}=0}$$
따라서, 아래에 있는 벡터 $\mathbf{H}$는 상수 벡터이다.
$$\mathbf{H} = \mathbf{r} \times \dot{\mathbf{r}} = r\mathbf{u} \times \frac{d}{dt}(r\mathbf{u}) = r\mathbf{u} \times (r\dot{\mathbf{u}}+\dot{r}\mathbf{u}) = r^2(\mathbf{u} \times \dot{\mathbf{u}}) + r\dot{r} \underbrace{ (\mathbf{u} \times \mathbf{u})}_{0} = r^2\mathbf{u} \times \dot{\mathbf{u}}$$
다시 아래와 같이 외적을 구한다.
$$\ddot{\mathbf{r}} \times \mathbf{H} = -\frac{\alpha}{r^2}\mathbf{u} \times (r^2\mathbf{u} \times \dot{\mathbf{u}}) = -\alpha\mathbf{u} \times (\mathbf{u} \times \dot{\mathbf{u}}) = -\alpha[\underbrace{(\mathbf{u}\cdot\dot{\mathbf{u}})}_{0}\mathbf{u}-(\mathbf{u}\cdot\mathbf{u})\dot{\mathbf{u}}]$$
여기서 $\mathbf{u}\cdot\mathbf{u} = |\mathbf{u}|^2 = 1$이므로 양변을 미분하여 $\mathbf{u}\cdot\dot{\mathbf{u}} = 0$이다.
$$\ddot{\mathbf{r}}\times\mathbf{H}=\alpha\dot{\mathbf{u}}\tag{16}$$
양변을 적분하자
$$\dot{\mathbf{r}}\times\mathbf{H}=\alpha\mathbf{u} + \mathbf{c}$$
$\mathbf{c}$는 $t$에 대한 상수 벡터이다.
$$\mathbf{r}\cdot(\dot{\mathbf{r}}\times\mathbf{H})=\mathbf{r}\cdot(\alpha\mathbf{u} + \mathbf{c}) = \alpha\mathbf{r}\cdot\mathbf{u} + \mathbf{r}\cdot\mathbf{c} = \alpha r(\mathbf{u}\cdot\mathbf{u})+rc\cos(\theta)=r(\alpha + c\cos(\theta)) $$
여기서 $\theta$는 두 벡터 $\mathbf{r}$과 $\mathbf{c}$가 이루는 각이다.
$$r = \frac{\mathbf{r}\cdot(\dot{\mathbf{r}}\times\mathbf{H})}{\alpha + c\cos(\theta)} = \frac{(\mathbf{r}\times\dot{\mathbf{r}})\cdot\mathbf{H}}{\alpha + c\cos(\theta)} = \frac{|\mathbf{H}|^2}{\alpha + c\cos(\theta)}$$
$\displaystyle{p=\frac{\mathbf{H^2}}{\alpha},\;\;e=\frac{c}{\alpha}}$라고 치환하여 정리하면 아래와 같이 타원의 방정식임을 확인할 수 있다.
$$r = \frac{p}{1 + e \cdot \cos \theta} $$
$\blacksquare$








