체바의 정리(Ceva Theorem)

평면에 있는 삼각형에서 아래와 같은 정리가 성립한다.

체바Ceva의 정리

주어진 삼각형 $ABC$에서 변 위에 있지 않은 정점 $O$를 지나는 직선 $AO$, $BO$, $CO$가 변과 만나는 점을 각각 $D$, $E$, $F$라고 할 때 방향이 있는 길이를 써서 나타내면 아래와 같은 관계가 성립한다.

$$\frac {AF}{FB} \cdot \frac {BD}{DC} \cdot \frac {CE}{EA} = 1.$$

이때, 세 선분 $AD$, $BE$, $CF$는 체비안으로 부른다.

방향이 있는 길이 $XY$는 $X$가 선의 고정된 방향에서 $Y$의 왼쪽 또는 오른쪽에 있는지 여부에 따라 양수 또는 음수로 정해진다. 예를 들어, $AF / FB$는 $F$가 $A$와 $B$ 사이에 있을 때 양의 값을 갖고 그렇지 않으면 음의 값을 갖는다.

이 정리는 역도 참이다. $BC$, $AC$, $AB$ 위에 있는 점 $D$, $E$, $F$가 아래를 만족하면 세 직선 $AD$, $BE$, $CF$는 한점에서 만나거나 서로 평행이다.

$$\frac{AF}{FB} \cdot \frac {BD}{DC} \cdot \frac {CE}{EA} = 1.$$

이 정리의 이름는 1678년 지오바니 체바(Giovanni Ceva)가 출판한 직사각형 선(De lineis rectis)에서 비롯되었지만 11세기 사라고사의 왕인 Yusuf Al-Mu'taman ibn Hűd가 훨씬 일찍 증명하였다.

넓이를 이용한 증명

먼저 세 비율이 모두 양수라서 좌변이 양수라고 하면 $O$는 삼각형 내부에 있다.[왼쪽 그림] 세 비율 가운데 하나는 양수이고 나머지 둘이 음수라면 점 $O$는 삼각형 외부에 있다.[오른쪽 그림]

삼각형 넓이는 밑변과 높이에 비례한다.

$$\frac{|\triangle BOD|}{|\triangle COD|}=\frac{BD}{DC}=\frac{|\triangle BAD|}{|\triangle CAD|}.$$

그러므로

$$\frac{BD}{DC}=\frac{|\triangle BAD|-|\triangle BOD|}{|\triangle CAD|-|\triangle COD|}=\frac{|\triangle ABO|}{|\triangle CAO|}.$$

마찬가지로

$$\frac{CE}{EA}=\frac{|\triangle BCO|}{|\triangle ABO|},$$

이고

$$\frac{AF}{FB}=\frac{|\triangle CAO|}{|\triangle BCO|}.$$

세 방정식을 변끼리 곱하면

$$\left|\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} \right|= 1.$$

$\blacksquare$

이 정리는 방정식이 부호만 다른 메넬라우스(Menelaus)의 정리와 매우 비슷하다. 메넬라우스(Menelaus) 정리로 증명할 수도 있다.

메넬라우스의 정리

삼각형 $ABC$와 $A, B, C$가 아닌 점 $D, E, F$를 지나는 할선이 주어졌을 때 아래와 같은 등식이 성립한다.

*transversal: 평면 위에 있는 두 직선과 서로 다른 두 점에서 만나는 직선인데 알맞은 우리말을 아직 찾지 못했다.

$$\frac {AF}{FB} \times{\frac {BD} {DC} \times \frac {CE} {EA}} =-1.\tag{1}$$

먼저 메넬라우스 정리를 증명하자.

세 꼭짓점 $A$, $B$, $C$에서 직선 $DEF$까지 거리를 각각 $a, \;\;b,\;\; c$라고 하자.

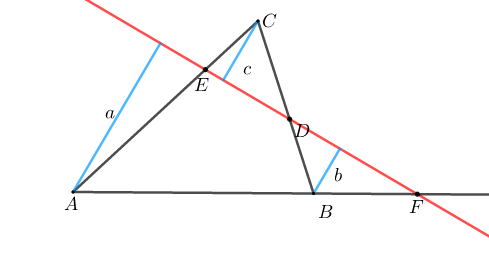
닮음비에 따라 길이만 생각한다면

$$|AF/FB| = |a/b|, \quad |BD/DC| = |b/c|, \quad |CE/EA| = |c/a|.$$ 

$$\left|\frac{AF}{FB}\right| \cdot \left|\frac{BD}{DC}\right| \cdot \left|\frac{CE}{EA}\right| = \left| \frac{a}{b} \cdot \frac{b}{c} \cdot \frac{c}{a} \right| = 1. $$

$\blacksquare$

직선 $DEF$가 모두 삼각형 외부에 있어도 증명은 다르지 않다.

다른 방법

$C$에서 $AB$에 평행하고 $DEF$와 $K$에서 만나는 직선 $CK$를 긋는다.

삼각형의 닮음에 따라

$$\left|\frac{BD}{DC}\right| = \left|\frac{BF}{CK}\right|,\,\left|\frac{AE}{EC}\right| = \left|\frac{AF}{CK}\right|$$

여기에서 $CK$를 소거하고 정리하면 (1)을 얻을 수 있다.

$\blacksquare$

정리의 역인 '방정식 (1)을 만족하는 점은 한 직선 위에 있다.'도 성립한다.

직선 $BC$, $AC$, $AB$ 위에 각각 점 $D$, $E$, $F$가 주어졌을 때 (1)을 만족한다고 하자.

점 $F^{\prime}$는 $AB$와 $DE$가 만나는 점이라고 하면

(1)은 $D$, $E$, $F^{\prime}$에 대해서도 성립한다.

둘을 비교하면

$$\frac{AF}{FB} = \frac{AF'}{F'B}.$$

따라서 $F=F^{\prime}$.

$\blacksquare$

체바 정리를 메넬라우스 정리로 증명하자.

메넬라우스 정리에 따라 삼각형 $ACF$에서 직선 $BOE$는

$$\frac{AB}{BF} \cdot \frac{FO}{OC} \cdot \frac{CE}{EA} = -1.$$

삼각형 $BCF$에서 직선 $AOD$는

$$\frac{BA}{AF} \cdot \frac{FO}{OC} \cdot \frac{CD}{DB} = -1.$$

두 등식을 변끼리 나누면 정리가 증명된다.

$\blacksquare$

예전에 수학 경시대회에 아주 자주 등장했던 정리인데 요즘은 잘 모르겠다. 말이 나온 김에 메넬라우스 정리를 쓰는 경시대회 문제 하나 남겨 둔다.

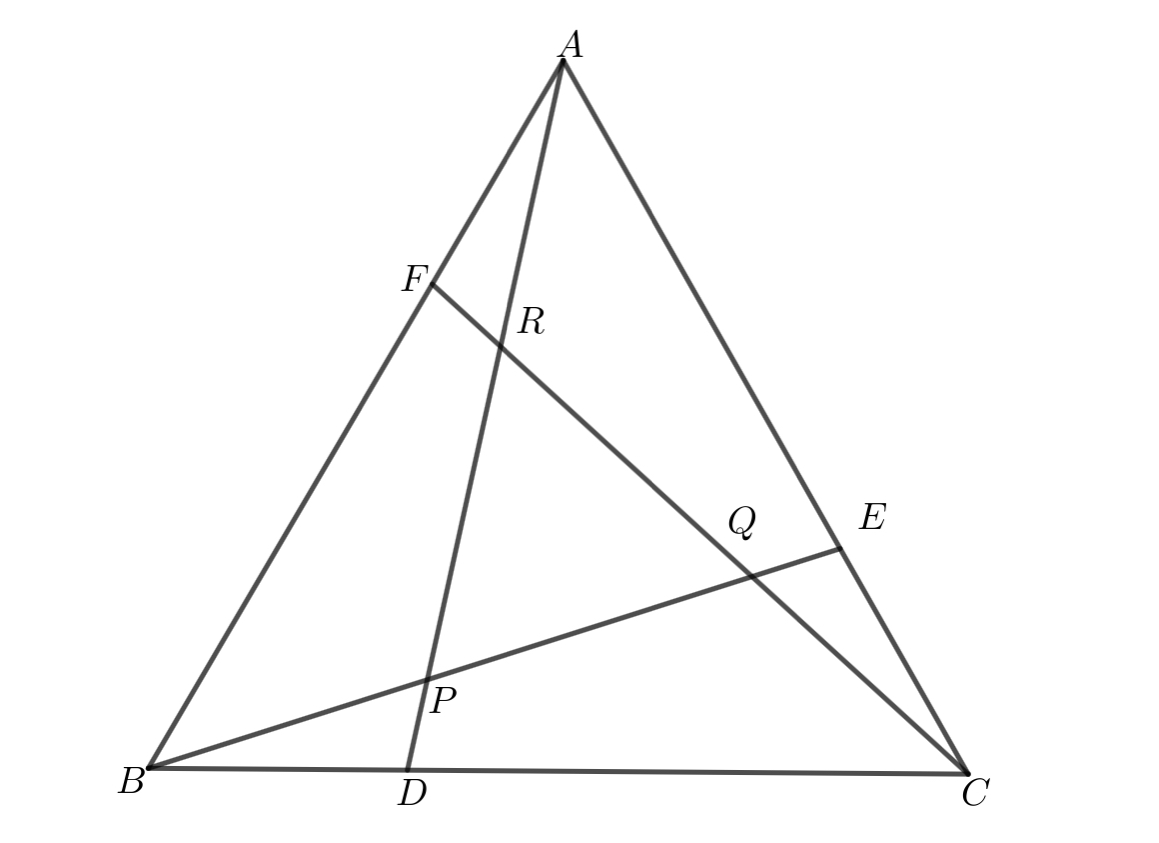
문제

정삼각형 $ABC$의 변 $BC,\;\;CA,\;\;AB$ 위에 내분점 $D$, $E$, $F$는 변을 $3:(n-3)\quad(n>6)$으로 나눈다. 선분 $AD$, $BE$, $CF$가 만나는 점 $P$, $Q$, $R$을 꼭짓점으로 하는 정삼각형 $PQR$의 넓이가 정삼각형 $ABC$ 넓이의 $4/49$이다. $n$을 구하여라.