니들이 삼각비를 알아?

수학에는 수많은 정의(definition)와 정리(theorem)가 있다. 개념이나 용어를 약속하는 정의는 매우 중요하므로 반드시 이해하고 외워두어야 한다. 중학교 교과서는 정의를 뜻이라고 적는다. 뜻도 모르고 쓰는 말은 무의미한 소리와 마찬가지다.

수학 교과서는 단원을 시작하면서 반드시 새로 나오는 용어의 뜻을 밝혀 둔다. 그런데 이 중요한 뜻을 대충대충 건성으로 읽고 넘어가는 학생이 너무 많다. 특히 학원에서 미리 배운 아이들은 수업 시간에 정의를 똑바로 알아야 한다고 강조해도 좀처럼 귀담아듣지 않는다.

삼각비의 뜻

중학교 3학년에서 삼각비를 배운다. 교과서는 삼각비를 아래와 같이 정의하고 있다.

동아출판 교과서에서

이렇게 정확하게 가르쳐도 '각 A에 대한 사인'이 무엇이냐고 물으면 '빗변 분의 높이'라는 대답이 훨씬 많이 나온다. 물론 야박하게 틀렸다고 하기는 좀 그렇다. 많은 문제집에서 쓰고 있지만 밑변이나 높이와 같은 용어는 오해를 불러오기 쉬운 말이므로 정의에선 쓰지 않는다. 그림에서 $\sin A$를 구할 때 $a$가 높이라는 말이 자연스럽지만 $\sin B$를 구할 때 $b$를 높이라고 말하는 것은 자연스럽지 않다. 따라서 수학 교과서는 정확하게 위와 같이 대변(각과 마주 보는 변)의 이름을 정하고 뜻을 밝혀두는 것이다.

수학을 공부할 때도 역사를 알고 말의 뿌리까지 알면 좋다. 아래와 같이 정의하면 어떨까? 무엇이든 공부를 시작할 때는 사전을 찾아 용어의 뜻을 정확하게 밝히면 좋다. 빗변은 영어로 hypotenuse인데 '잡아당기다', '뻗다'란 말에 뿌리를 두고 있다. 마주 보는 opposite와 인접한 adjacent까지 사전을 찾아보면 더욱 좋다. 

 

$$\sin A= \frac{a}{h},\quad \cos A=\frac {b}{h},\quad \tan A=\frac{a}{b}$$

이제 사인이 무엇이냐는 물음에는 '빗변의 길이 분의 대변의 길이'라고 대답하자. 조금 더 똑똑해 보인다. 빗변은 직각의 대변이므로 높이나 밑변과 같이 혼란스러운 용어가 아니다. 2학년에서 배웠듯이 직각삼각형에서 외심은 빗변의 중점이다.

사인(sine)은 원의 현(弦, chord)과 관계있다. 인도 천문학자가 현의 절반을 산스크리스트어 jya-ardha로 적었고, 간단하게 jya 또는 jiva로 적었다. 이를 옮긴 아랍 수학책은 jiba로 적었는데 이를 옮기던 사람이 jaib(자이브:옷의 주름, 바다의 만)으로 잘못 알고 sinus(라틴어 : 옷의 주름, 만)으로 옮겨 적었다. 아랍어는 모음을 쓰지 않고 자음만 적는다. 요즘 유행하는 초성 퀴즈를 생각하면 된다.  jiba와 jaib를 모두 jb로 적기때문에 이를 번역하는 사람이 실수할 가능성이 매우 크다. sinus가 영어 sine로 바뀌었으니 어찌 보면 잘못된 이름을 쓰고 있는 셈이다.

 

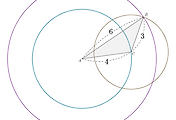
위 그림에서 $\angle A=\angle BOD$이므로

$$\sin A=\frac{\overline{BC}}{\overline{AB}}=\frac{\overline{BD}}{\overline{OB}}$$

촌스럽지만 많이 쓰이는 삼각비를 외우는 방법

크기가 특별한 각($30^{\circ}$, $45^{\circ}$, $60^{\circ}$)의 삼각비

정삼각형과 정사각형을 이등분해서 만든 삼각형의 변의 길이를 구해보자.

1) 정삼각형을 이등분

각이 30도와 60도인 직각삼각형

2) 정사각형을 이등분

직각이등변 삼각형

$$A$$	$$\sin A$$	$$\cos A$$	$$\tan A$$
$$30^{\circ}$$	$$\frac{1}{2}$$	$$\frac{\sqrt3}{2}$$	$$\frac{\sqrt3}{3}$$
$$45^{\circ}$$	$$\frac{\sqrt2}{2}$$	$$\frac{\sqrt2}{2}$$	$$1$$
$$60^{\circ}$$	$$\frac{\sqrt3}{2}$$	$$\frac{1}{2}$$	$$\sqrt3$$

위에 있는 두 삼각형은 우리에게 아주 익숙한 삼각자 모양이다. 이른바 특수각의 삼각비는 모두 외우고 있어야 편하다. 고등학교에서 배우는 것이긴 하지만 이미 이름의 유래를 통해 알게 된 코사인이 여각의 사인임을 안다면 외우는데 조금 도움이 된다. 

$$\cos A=\sin (90^{\circ}-A)$$

정오각형을 잘라서 삼각형을 만들면 크기가 $18^{\circ},36^{\circ},72^{\circ}$인 각에 대한 삼각비의 값을 알 수 있다. 황금비를 조금 더 확실하게 관찰하고 이해할 수 있다는 점은 도움이 되겠다. 도전하고 싶다면 도전해 보시라.

삼각비와 삼각함수는 조금 다르지만 맛보기로 고등학교에서 등장하는 몇몇 공식을 구경해 보자. 삼각비는 피타고라스 정리에서 나온다고 생각할 수 있다. 맨 위에 있는 그림 $\angle C=90^{\circ}$이므로 피타고라스 정리는 아래와 같이 적을 수 있다.

$$c^2=a^2 +b^2\tag{1}$$

$$1=\left(\frac{a}{c}\right)^2 +\left(\frac{b}{c}\right)^2 $$

$$1=\sin^2 A+\cos^2 A\tag{2}$$

$$\tan A=\frac{a}{b}=\frac{\sin A}{\cos A}\tag{3}$$

예각의 삼각비

반지름의 길이와 반으로 나눈 현의 길이 사이의 비로써 삼각비를 나타내면 예각의 삼각비를 쉽게 이해할 수 있다.

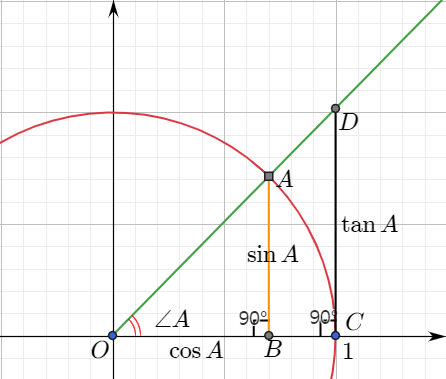
반지름이 1인 사분원을 좌표평면에 그려보자. 원 위에 있는 점 $A$와 반직선 $OA$를 생각하자. 점 $A$에서 $x$축에 내린 수선의 발을 $B$라고 하고 점 $(1,0)$에서 $x$축과 수직인 직선이 반직선 $OA$와 만나는 점을 $D$라고 하면 삼각비는 선분의 길이로 나타낼 수 있다. 

$$\sin A=\overline{AB},\quad\cos A=\overline{OB},\quad\tan A=\overline{CD}$$

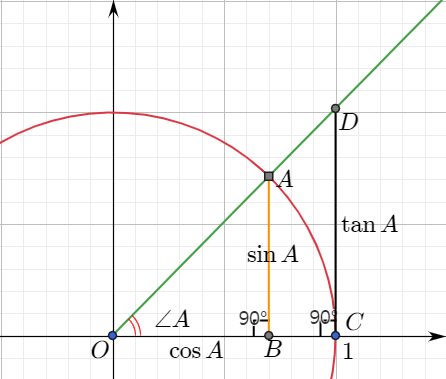
이것을 삼각비의 정의로 생각해도 된다. 실제로 고등학교에서 배우는 삼각함수는 각의 동경이 반지름의 길이가 $r$인 원과 만나는 점 $A$의 좌표로 삼각함수를 정의한다. $$A(r\cos A, r\sin A)$$

각의 크기와 삼각비의 값 사이의 관계를 생각해 보자. 특히 각의 크기가 $0^{\circ},\;\;90^{\circ}$일 때 삼각비의 값을 쉽게 알 수 있다.

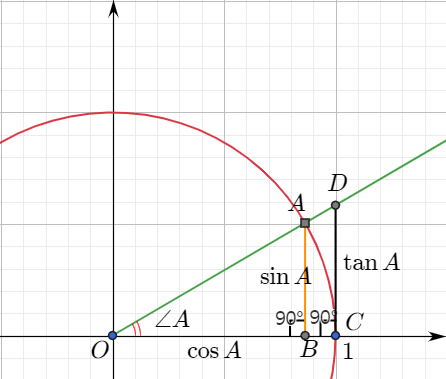
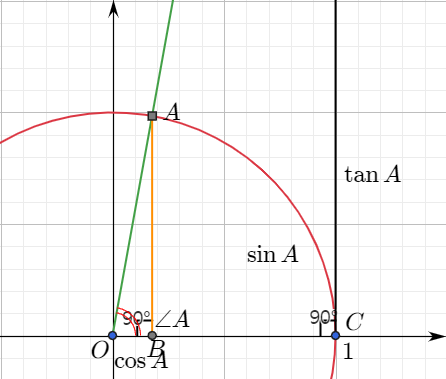
$0^{\circ}$이면 점 $A$, $B$, $C$, $D$는 모두 점 $C(1,0)$과 포개진다.

$$\sin 0^{\circ}=0,\;\;\cos 0^{\circ}=1,\;\;\tan 0^{\circ}=0$$

$90^{\circ}$ 이면 점 $A$는 점 $(0,1)$과 점 $B$는 점 $(0,0)$과 포개진다. 직선 $CD$는 직선 $OA$와 평행이 되므로 교점 $D$는 찾을 수 없다.

$$\sin 90^{\circ}=1,\;\;\cos 90^{\circ}=0$$

아래 더보기를 열면 삼각비를 부르는 다른 이름의 유래를 알 수 있다. 고등학교 과정에서 정의하는 삼각함수를 보고 싶다면 연결고리를 따라가면 된다.

co-sine에서 co는 나머지(complementary)를 뜻한다. 나머지 각에 대한 사인이 바로 코사인(cosine)이다. 1620년 군터가 complementum sinus를 합친 co.sinus로 썼고 1658년에 뉴턴은 cosinus로 적었다. 1729년 오일러가 cos으로 적은 것이 오늘날까지 이어졌다.

탄젠트(tangent)는 만진다는 라틴말(tangens)에서 왔다. 사인이나 코사인처럼 각에 대한 함수가 아니라 어떤 물체의 그림자 길이에서 높이를 계산하는 데서 출발했다. 중세에는 움브라 렉타(umbra recta: 바른 그림자, 수직으로 세운 막대가 수평면에 드리우는 그림자)와 움브라 베르사(umbra versa: 반대 그림자, 수평으로 된 막대가 수직면에 드리우는 그림자)와 같이 그림자와 관련된 이름으로 불렸으며(이들 라틴어 이름도 아랍어 책을 번역하면서 만들어진 것이다), 이 개념을 접선의 기울기와 연관 지어 탄젠트라고 부른 것은 덴마크 수학자 토마스 핀케(Thomas Fincke, 1561-1656)가 최초이다.

직각삼각형에서 정의한 삼각비는 예각일 때만 생각할 수 있다. 이 삼각비를 일반화하여 조금 더 쓸모 있는 함수로 만들기 위해 먼저 각을 일반화하고 새롭게 정의한다. 그것이 호도법 다시 말해 라디안(radian)이다. 반지름으로 호의 길이를 재는 것이 라디안(radius+angle)이다. 삼각비는 원에서 정의하기 시작했기에 삼각함수를 원함수로 부르기도 한다.

https://suhak.tistory.com/167

삼각비와 삼각함수