가우스 정17각형이 작도 가능함을 보이다

작도는 눈금 없는 자와 컴파스만으로 도형을 그리는 일이다. 그리스 수학에서 시작한 작도는 오랫동안 기하학의 기본이었다. 유클리드 '원론'은 작도로 증명하는 것과 마찬가지다. 간단한 증명을 보자.

원론 1권

명제 1 정삼각형을 그릴 수 있다.

 

명제 2 주어진 점에서 시작하여 주어진 선분과 같은 선분을 그릴 수 있다.  

명제 1에서 증명한 바에 따라 점 $D$를 작도하고 직선 $DA$, $DC$를 긋는다.

$A$를 중심으로 반지름 $\overline{AB}$인 원을 그려 점 $F$를 찾고 점 $D$를 중심으로 반지름 $\overline{DF}$인 원을 그린다.

 $\overline{AD}=\overline{CD}$이므로 $C$를 중심으로 반지름 $\overline{CG}$인 원을 그리면 $C$에서 시작하는 주어진 선분과 길이가 같은 선분을 그릴 수 있다.

이 명제를 증명함으로써 컴파스로 길이를 옮길 수 있다고 보는 것이다.

정5각형은 아래와 같이 작도할 수 있다. 정오각형을 작도함으로써 정15각형도 작도할 수 있다. 정5각형은 흥미로운 사실을 많이 품고 있다. 여기에 정오각형에 얽힌 이야기를 적는다.

 

1. 정오각형은 황금비(golden section)를 품고 있다.
 아래 그림에서

 

$$a:b-a=b:a$$

$$a^2 =b^2 -ab$$

$$\left(\frac{b}{a}\right)^2 -\frac{b}{a}-1=0$$  

$$\frac{b}{a}=\frac{1+\sqrt5}{2}$$



2. 한 변의 길이가 $1$일 때, 대각선의 길이는 $\displaystyle{\frac{1+\sqrt {5}}{2}}$이므로 아래와 같이 작도할 수 있다.



3. 외접원이 주어질 때는 아래와 같이 작도할 수 있다.

   

   
   

외접원 반지름을 $1$이라고 가정한다면 정오각형을 작도하는 일은 단위원 $x^2 +y^2 =1$ 위에 한 점 $(1,0)$을 잡고 원주 위에 있는 나머지 꼭짓점의 좌표를 구하는 일과 같다.

이것은 방정식 $x^5 =1$의 복소수 해를 구하는 것과 같다.

$(x-1)(x^4 +x^3 +x^2 +x+1)=0$이므로 $x^4 +x^3 +x^2 +x+1=0$의 해를 구하면 된다.

이제,  $x^4 +x^3 +x^2 +x+1=0$의 해를 $z$라고 하자.

$z^4 +z^3 +z^2 +z+1=0$에서

$\displaystyle{z^2 +z +1 +\frac{1}{z}+\frac{1}{z^2}=0}$이다. 이를 정리하면

$\displaystyle{\left(z +\frac{1}{z}\right)^2+\left(z+\frac{1}{z}\right)-1=0}$

$\displaystyle{t=z+\frac{1}{z}}$

$t^2 +t-1=0$이므로 $\displaystyle{t= \frac{-1\pm\sqrt {5}}{2}}$이다.

$z^2 -tz+1=0$에서 $\displaystyle{z= \frac{t\pm\sqrt {t^2-4}}{2}}$이다.

한편, $z=\cos \theta +i\sin\theta$로 놓으면 주어진 드므아브르 정리에 따라

$\cos 5\theta +i\sin5\theta=1$

$5\theta =2n\pi$에서 근은 $\displaystyle{\theta_n =\frac{2n\pi}{5},\quad (n=0,1,2,3,4)}$임을 쉽게 알 수 있다.

$x$좌표는 실수부만 생각하면 되므로

$\displaystyle{\cos \frac{2\pi}{5} =\cos \frac{8\pi}{5}=\frac{-1+\sqrt5}{4}}$

$\displaystyle{ \cos \frac{4\pi}{5} =\cos \frac{6\pi}{5}=\frac{-1-\sqrt5}{4}}$이다.



4. 일반적으로 정다각형의 작도 가능성에 대해 살펴보자.

정$n$각형을 작도하는 일은 방정식 $x^n -1=0$의 해를 구하는 일과 같다.

이것은 $\displaystyle{\cos\frac{2\pi}{n}}$을 구하는 것과 같다.

이제, 정$3$각형과 정$4$각형이 작도 가능이고 각을 이등분하는 것도 작도 가능이므로 정$3\cdot 2^n$과 정$4\cdot 2^n$각형은 작도 가능하다. ($n=0,1,2,3,\cdots$) $\displaystyle{\frac{2\pi}{3}-\frac{2\pi}{5}=\frac{4\pi}{15}}$이므로 정 $15$각형은 작도할 수 있다. 유클리드 '원론' 4권 명제16은 정$15$각형의 작도법이다.

아래와 같은 정$n$각형은 작도 가능하다.

3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257, 272...

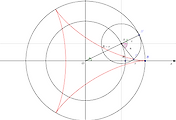
가우스는 19살에 정17각형이 작도 가능함을 보였고 5년 뒤엔 $n$이 홀수인 서로 다른 페르마 소수($\displaystyle{F_n =2^{2^n}+1}$) 곱으로 나타내어진다면 작도가능함을 밝혔다.

이제 $\displaystyle{p =2^{2^n}+1}$이라고 하자.

$x^{2^n+1}-1=0$

$(x-1)(x^{2^n }+x^{2^n -1}+\cdots+x+1)=0$

$x^{2^n }+x^{2^n -1}+\cdots+x+1=0$의 한 근을 $\zeta$로 놓으면

$\zeta^{p-1}+\zeta^{p-2}+\zeta^{p-3}+\cdots+\zeta^{2}+\zeta+1=0$ 

이식은 $n$ 차례 치환하면 이차식으로 바꿀 수 있다.

바꾸는 방법은 $(n+1)^k\equiv m\;\;(mod\;\;p), \;\;k,m=0,1,2,\cdots,p-1$을 만족하는 음이 아닌 정수 $m$을 찾아 $\zeta^m$의 차례를 정하고 이 차례를 $2^n\;\;(n=1,2,3,\cdots,n)$으로 나눈 나머지가 같은 것끼리 짝을 맺어 바꾼다.

바꾸는 방법은 아래 17각형의 작도를 참고하자.

5. 정12면체는 정오각형으로 이루어졌다. 정오각형을 제대로 배웠다면 정12면체 이면각의 코사인을 구할 수 있을 것이다.

***

수학노트에서 옮김.

1796년 열 아홉 살 난 가우스는 정17각형이 아래와 같이 작도 가능함을 대수적으로 증명하였다.

$z^{16}+z^{15}+\cdots+z+1=0$의 풀이를 반복적인 2차방정식의 풀이로 바꿀 수 있는가의 문제

16차 방정식을 2차방정식 네번 푸는 문제로 바꾸는 것

이 아이디어를 좀더 간단한 예를 통해 이해하기 위해서는 정오각형 항목 중 꼭지점의 평면좌표를 참조

증명 $\displaystyle{\zeta=e^{2\pi i \over 17}=\cos \frac{2\pi}{17}+i \sin \frac{2\pi}{17} }$로 두자. 참고 세상에서 가장 아름다운 수식 

이 값을 대수적으로 구하는 것이 목표. $2^{2^2} =16$이므로 두 차례 치환하면 이차식으로 바꿀 수 있다.

$$(3^1, 3^2,3^3, 3^4, 3^5, 3^7, 3^8, 3^9, 3^{10}, 3^{11}, 3^{12}, 3^{13}, 3^{14}, 3^{15}, 3^{16}) \equiv (3, 9, 10, 13, 5, 15, 11, 16, 14, 8, 7, 4,12, 2, 6, 1) \pmod {17}$$

이 순서대로 $2$로 나눈 나머지에 따라서 분류

$A_0 = \zeta^{9} + \zeta^{13} + \zeta^{15} + \zeta^{16}+\zeta^{8} + \zeta^{4} + \zeta^{2} +\zeta^{1}$

$A_1 = \zeta^3 + \zeta^{10} + \zeta^{5} + \zeta^{11}+\zeta^{14} + \zeta^{7} + \zeta^{12} +\zeta^{6}$

$A_0+A_1= -1, \quad A_{0}A_{1} = -4, A_0>A_1$

$\displaystyle{A_0 = \frac{-1 + \sqrt{17}}{2} , A_1= \frac{-1 - \sqrt{17}}{2}}$

이번에는 $4$로 나눈 나머지에 따라서 분류

$B_0 = \zeta^{13}+ \zeta^{16}+ \zeta^4 + \zeta^1$

$B_1= \zeta^3 + \zeta^5 + \zeta^{14} + \zeta^{12}$

$B_2= \zeta^9 + \zeta^{15} + \zeta^8 +\zeta^2$

$B_3 =\zeta^{10} + \zeta^{11} + \zeta^{7} +\zeta^{6}$

$B_0+B_2=A_0, \quad B_0B_2= -1, B_0>0$

$\displaystyle{B_0 = \frac{-1 + \sqrt{17} + \sqrt{34 - 2\sqrt{17}}}{4}, B_2 = \frac{-1 + \sqrt{17} - \sqrt{34 - 2\sqrt{17}}}{4} }$

$B_1+B_3=A_1, \quad B_1B_3= -1, B_{1}> 0$

$\displaystyle{B_1 = \frac{-1 - \sqrt{17} + \sqrt{34 + 2\sqrt{17}}}{4}, B_3 = \frac{-1 - \sqrt{17} - \sqrt{34 + 2\sqrt{17}}}{4}}$

이번에는 $8$로 나눈 나머지에 따라서 분류

$C_0= \zeta^{16}+ \zeta^1, \quad C_4= \zeta^{13} +\zeta^4, C_0 > C_1$

$C_0+C_4=B_0, C_0C_4=B_1$

$\displaystyle{C_0= \frac{B_0+\sqrt{B_0^2-4B_1}}{2}= \frac{-1+\sqrt{17}+\sqrt{34-2\sqrt{17}}+ \sqrt{68+12\sqrt{17}-4{\sqrt{170+38\sqrt{17}}}} }{8}}$

$\displaystyle{C_4= \frac{B_0 - \sqrt{B_0^2-4B_1}}{2}}$

이제 마무리

$\displaystyle{\zeta =\frac{{C_0} + \sqrt{{C_0}^2 - 4}}{2} }$

$\displaystyle{\cos \frac{2\pi}{17}= \frac{-1+\sqrt{17}+\sqrt{34-2\sqrt{17}}+ \sqrt{68+12\sqrt{17}-4{\sqrt{170+38\sqrt{17}}}} }{16}}$

 

가능함은 가우스가 보였지만 1825년이 되어서야 Johannes Erchinger가 실제 작도법을 보일 수 있었다. 아래와 같은 또 다른 작도법은 Carlyle가 찾았다.

위키백과 정17각형 작도

위키백과 작도

construct.pdf