순열(permutation)에서 조합(Combination)으로

순서가 있는 것에서 없는 것으로

경우의 수를 세는 방법 가운데 바탕이 되는 것은 순열과 조합이다. 그 가운데에서 순열이 밑바탕이다. 먼저 `1,2,3,4,5`로 만들 수 있는 다섯자리 자연수는 몇 개일까? $5!$이다. 이 가운데 셋을 뽑아 만들 수 있는 자연수는 아래와 같이 `5×4×3`이다. 이를 기호로 $\displaystyle{{}_5 P_3}$이라고 적는다.

이것은 다섯자리 자연수 일의 자리와 십의 자리 수를 모두 `0`으로 바꾼 것과 같으므로 $\displaystyle{\frac{5!}{2!}}$이다. 이와 같이 순서가 있는 것을 순서가 사라지도록 만들려면 같아지는 개수로 나누는 것이다.

이를 일반화하면 $\displaystyle{{}_n P_r =\frac{n!}{(n-r)!}}$ 이다.

같은 것이 있는 순열에서 조합으로

`a a a b b `를 일렬로 나열하는 방법은 어떻게 셀까? 이는 모두가 다르다고 생각한 다음 같아지는 것들의 순서를 사라지게 하면 된다. 다시 말하면 `a_1 , a_2 ,a_3 ,b_1 ,b_2 `를 나열하는 경우의 수 `5!`을 $\displaystyle{ 3!\times2!}$으로 나누면 된다. $\displaystyle{ \frac{5!}{3!2!}}$인데 이것은 서로 다른 5개 가운데 3개를 뽑는 경우의 수와 같다. 이는 $\displaystyle{{}_5 P_3}$ 에서 뽑힌 세 수의 순서를 없앤 것과 같아진다.

순서가 사라진 순열을 조합(Combination)이라 하고 ${}_5 C_3$이라고 쓴다. $\displaystyle{ \frac{{}_5 P_3}{3!}=\frac{5!}{2! 3!}}$ 와 같이 셈한다. 이를 일반화하면 $\displaystyle{{}_n C_r= \frac{{}_n P_r}{r!}= \frac {n!}{r!(n-r)!}}$ 이다.

https://suhak.tistory.com/1234

원순열

이제 동그란 탁자에 둘러 앉는 경우의 수를 생각하자. 다섯 사람이 동그란 탁자에 둘러 앉는 방법은 `4!`이다.원이 $5$번 돌아가면 겹치는 순열 다섯을 하나로 보아야하기 때문이다.

예를 들면 $12345, 23451, 34512, 45123, 51234$는 다른 순열이지만 원으로 만들면 같은 순열이다. 따라서 $\frac{5!}{5}=4!$이다.

일반적으로 서로 다른 `n`개를 원탁에 늘어놓는 순열은 `(n-1)!`이다.

하지만 순열이 순환하는 순열이 있다면 이야기가 달라진다.
` a a b b `로 이루어진 순열은 모두 6개가 있다. 모두 적어보면 `a a b b`, `ab ba`, `b ba a`,` ba ab`,` abab`,` baba`이다. 이 가운데 앞에 있는 넷은 순환하지 않는 순열이므로 원으로 만들면 한 가지 순열이다. 뒤편 둘은 순환마디가 $2$인 순열이므로 마찬가지 한 가지 원순열이다.

보통 `n`개를 늘어놓은 원순열에서 순환하지 않으면 끊어서 선으로 만들때 `n`가지 순열이 나온다. 그러나 순환마디 길이가 `m`이라면 선으로 만들면 `m`가지 순열이 나온다.

따라서 보다 정확하게 원순열을 말하면 한줄로 늘어선 순열에서 순환하지 않는 것과 순환하는 것을 따로 세고 순환마디의 길이가 `m`일 때,

원순열의 개수 `=`순환하지 않는 개수$\displaystyle{ \times \frac{1}{n}+}$ 순환하는 개수$\displaystyle{ \times \frac{1}{m}}$ 이다.

이쯤되면 머리가 좀 아프기 시작한다. 다행스럽게도 고등학교에서 순환하는 것이 들어있는 것은 다루지 않는다.

목걸이순열

원순열을 목걸이라고 생각하면 뒤집을 수도 있으므로 또 달라진다. 여기에선 원순열과 목걸이순열 사이 관계를 알아보자. 대칭인 원순열과 비대칭인 원순열이 다르다. 대칭은 `1:1`로 비대칭은 `2:1` 로 대응된다. 따라서 목걸이 순열과 원순열 사이 관계를 정리하면 아래와 같다.

목걸이 순열의 수`=`대칭 원순열의 수`+`비대칭 원순열의 수$\displaystyle{ \times \frac{1}{2}}$

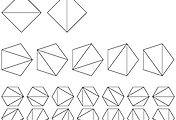
문제1.  $aabbc$로 이루어진 순열, 원순열, 목걸이 순열의 수를 구해보자.
1. 같은 것이 있는 순열이므로 $\displaystyle{ \frac{5!}{2!2!}=30}$이다.

2. 순환하는 순열은 없으므로 원순열은 $\displaystyle{ \frac{30}{5}=6}$이다.

3. 원순열 가운데 대칭인 것은 둘 $(5,6)$이 있으므로 목걸이 순열은 $\displaystyle{ 2+4\times\frac{1}{2}=4}$이다. 위 그림에서 $1$과 $2, 3$과 $4$는 같은 목걸이이다.

이제 원순열과 목걸이순열이 어우러진 문제를 풀어보자.

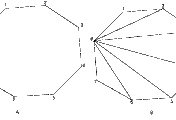
문제2. 그림과 같은 정육면체에 $123456$을 적어 넣는 방법은 모두 몇 가지일까?
꼭지점에 달아놓은 번호를 보고 아래와 같이 움직여 보자.
$1 \rightarrow 8, 2\rightarrow 7, 4\rightarrow 5, 3\rightarrow 6$ 처럼 뒤집는 경우 2가지
$1\rightarrow 2\rightarrow 3\rightarrow 4 , 5\rightarrow 6\rightarrow 7\rightarrow 8$처럼 돌리는 경우 4가지
$2\rightarrow 7\rightarrow 4, 1\rightarrow 6\rightarrow 8$ 처럼 `3,5`를 잡고 돌리는 경우 3가지
는 각각 하나씩으로 포개지므로 같아진다.
따라서 $\displaystyle{\frac{6!}{2\times 4\times3}=30}$이다.

$aabcde$를 써 넣는 방법은 몇 가지인가?
같은 것이 둘 있으므로 $\displaystyle{ \frac{30}{2}=15}$이다.

둘러보면 좋은 누리집
하나....maths is fun