벡터의 수직과 평행

벡터는 물리에서 시작했다. 물리량은 길이와 넓이, 질량처럼 크기만 있는 양과  힘과 일, 무게처럼 크기와 방향을 함께 가지는 양이 있다. 속력(speed)처럼 크기만 있는 양을 스칼라(scalar), 속도처럼 크기와 방향을 함께 가지고 있는 양을 벡터(vector)라 한다. 따라서 벡터를 나타낼 때는 크기와 함께 방향까지 나타내야 한다. 평면이나 공간 벡터는 화살표를 쓰면 쉽게 크기와 방향을 모두 나타낼 수 있다. 이때 화살표가 어떤 기준선과 이루는 각은 방향을 나타내는 좋은 도구가 된다.

예를 들면 길이가 4이고 $x$축 양의 방향과 이루는 각이 $\displaystyle{\frac{\pi}{3}}$라고 나타낸다. 당구장은 벡터 세상이다.

 

벡터가 스칼라와 다른 점은 방향이 있다는 것이다. 그러므로 벡터에서는 벡터가 이루는 각이 중요하다. 그 가운데서 수직일 때와 평행일 때가 아주 중요하다. 수직과 평행은 아래와 같이 정의한다.

두 벡터 $\vec{a}, \vec{b}$가 이루는 각이 $\displaystyle{\frac{\pi}{2}}$이면 $\vec{a}$와 $\vec{b}$는 서로 수직이라고 하고 $$\vec{a}\bot \vec{b}$$로 적는다.

두 벡터 $\vec{a}, \vec{b}$가 방향이 서로 같거나 반대이면 다시 말해 이루는 각이 $0$이거나 $\pi$이면 $\vec{a}$와 $\vec{b}$는 서로 평행이라고 하고 $$\vec{a}//\vec{b}$$로 적는다.

두 벡터가 이루는 각을 $\theta$라고 하면 내적은 $\vec{a}\cdot\vec{b}= |\vec{a}||\vec{b}|\cos\theta$이므로 내적을 이용하면 $\theta$를 쉽게 알아낼 수 있다.

$$\cos\theta=\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}$$

위에 있는 정의에 따라 수직할 때와 평행할 때를 방정식으로 적어보자.

영벡터가 아닌 서로 다른 두 벡터 $\vec{a},\vec{b}$가 있을 때.

$\vec{a}\bot \vec{b}$이면 $\vec{a}\cdot\vec{b}$이고 $\vec{a}//\vec{b}$이면 $\vec{a}\cdot\vec{b}=\pm|\vec{a}||\vec{b}|$이다. 한편 $\vec{a}//\vec{b}\iff\vec{a}=t\vec{b}$이다.

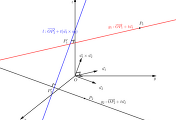
이제 한 점 $P_1$을 지나고 $\vec{u_1}=(l.m.n)$에 평행인 직선 $g_1$의 방정식을 구해보자.

아래 그림에서 직선 $g_1$ 위의 점을 $P(x,y,z)$라고 하자.

위에 적은대로 $\vec{P_1P}//\vec{u_1}$이므로 이를 방정식으로 적으면 $$\vec{P_1P}=t\vec{u_1}$$이고 이를 위치벡터로 나타내면

$$\vec{OP}-\vec{OP_1}=t\vec{u_1}$$이다. 정리하면

$$g_1:\vec{OP}=\vec{OP_1}+t\vec{u_1}$$

 

성분으로 정리하면 $(x,y,z)=(x_1 ,y_1, z_1)+t(l,m,n)$이다. $lmn \not=0$라면 $t$를 소거하여 아래와 같이 적을 수 있다.

$$\frac{x-x_1}{l}=\frac{y-y_1}{m}=\frac{z-z_1}{n}$$

$\vec{u_1}$은 방향벡터로 부른다.

 

다음으로 한 점 $P_1$을 지나고 $\vec{n}=(a,b,c)$에 수직인 평면 $\alpha$의 방정식을 구해보자.

$\vec{P_1P}\bot\vec{n}$이므로 이를 방정식으로 적으면 $$\vec{P_1P}\cdot\vec{n}=0$$이고 이다.

 

마찬가지로 성분으로 정리하자.

$$(x-x_1,y-y_1,z-z_1)\cdot(a,b,c)=0$$

$$ax+by+cz-(ax_1+by_1+cz_1)=0$$이다. 간단하게 정리하기 위해 $d=-(ax_1+by_1+cz_1)$라고 하면

$$ax+by+cz+d=0$$이다.

$\vec{n}$은 법선벡터로 부른다.

이와 같이 벡터의 수직과 평행을 제대로 파악하는 것이 벡터를 이해하는 지름길이다.