평면 곡선 운동에 관하여

포물선 운동

질량 $m$인 물체를 속도 $\mathbf{v_0}$로 쏘아 올렸다. 이 물체는 어떻게 움직일까?

먼저 시각 $t$일 때, 위치벡터를 $\mathbf{r}$이라고 하자.

$t=0$일 때 속도벡터 $\mathbf{v_0}$와 지면이 이루는 각을 $\alpha$라고 하면 아래와 같은 식이 성립한다.

$$\mathbf{v_0}=|\mathbf{v_0}|\cos\alpha\mathbf{i}+|\mathbf{v_0}|\sin\alpha\mathbf{j}$$

$$\mathbf{r_0}=0\mathbf{i}+0\mathbf{j}$$

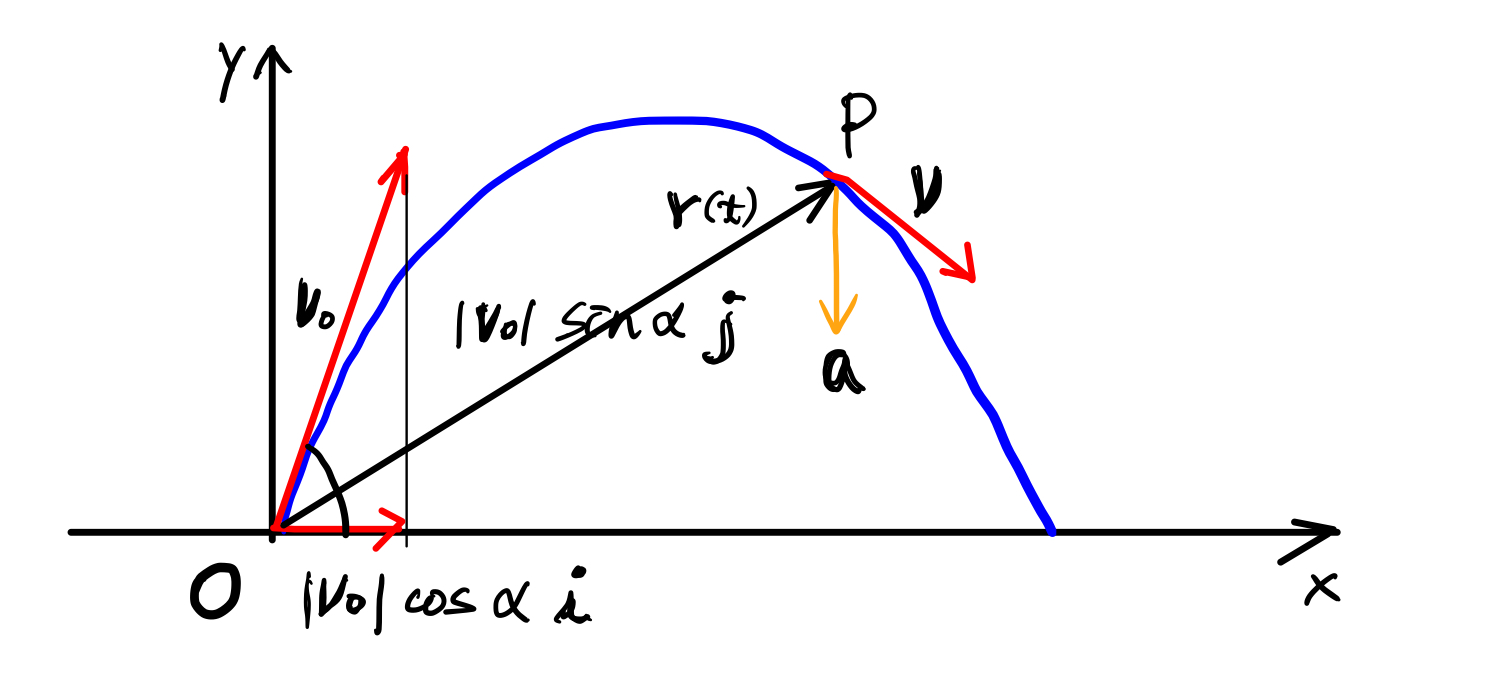
뉴턴 제2 운동법칙에 따라 물체가 받는 힘은 $F=m\mathbf{a}$이다. 한편 이 운동의 가속도는 중력가속도 $g$와 같다.

$$m\mathbf{a}=-mg\mathbf{j}$$

정리하면 아래와 같은 미분방정식을 얻는다.

$$\frac{d^2 \mathbf{r}}{d t^2}=-g\mathbf{j}$$

양변을 적분하자.

$$\frac{d \mathbf{r}}{d t}=-gt\mathbf{j}+C$$

$$\frac{d \mathbf{r}}{d t}=-gt\mathbf{j}+\mathbf{v_0}$$

$$ \mathbf{r}=-\frac{1}{2}gt^2\mathbf{j}+\mathbf{v_0}t+\mathbf{r_0}$$

$$ \mathbf{r}=-\frac{1}{2}gt^2\mathbf{j}+|\mathbf{v_0}|t\cos\alpha\mathbf{i}+|\mathbf{v_0}|t\sin\alpha\mathbf{j}+\mathbf{r_0}$$

$$ \mathbf{r}=|\mathbf{v_0}|t\cos\alpha\mathbf{i}+\bigg(|\mathbf{v_0}|t\sin\alpha\mathbf-\frac{1}{2}gt^2\bigg)\mathbf{j}+\mathbf{r_0}$$

원운동

점 $P$가 반지름이 $r$인 원을 따라 운동하고 있다고 하자.

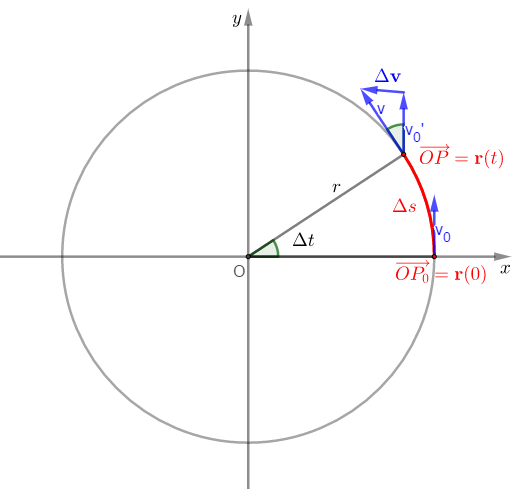
원운동을 하게 만드는 힘을 구심력이라 하자. 구심력을 구하기 위해 먼저 가속도를 구해보자. 

$$a=\lim_{\Delta t\rightarrow 0}\frac{\Delta v}{\Delta t}=\lim_{\Delta t\rightarrow 0}\frac{\mathbf{v}(t+\Delta t)-\mathbf{v}(t)}{\Delta t}$$

$t=0$일 때 속도는 $\mathbf{v_0}$라 하자.

그림에서 속도의 변화량 $\Delta \mathbf{v}=\mathbf{v}(t+\Delta t)-\mathbf{v}(t)$에 주목하자.

두 속도벡터 $\mathbf{v,v_0}$가 이루는 각은 두 벡터 $\overrightarrow{OP}, \overrightarrow{OP_0}$가 이루는 각 $\Delta t$와 같다.

$\Delta t\rightarrow 0$일 때, $|\Delta \mathbf{v}|:|\mathbf{v}|$의 극한은 $\Delta s:|\overrightarrow{OP}|$의 극한과 같을 것이다.

$$\Delta v:v\approx \Delta s:r$$

$$\Delta v:v\approx v\Delta t:r$$

$$r\Delta v\approx v^2 \Delta t$$

$$\frac{\Delta v}{\Delta t}\approx \frac{v^2}{r}$$

$$\lim_{\Delta t\rightarrow 0}\frac{\Delta v}{\Delta t}=\frac{v^2}{r}$$

$$a=\frac{v^2}{r}$$

이제 뉴턴 운동법칙에 따라 구심력을 구하면 된다.

$$F=ma=m\times \frac{v^2}{r}=\frac{mv^2}{r}$$

이제 위에 정리한 것을 벡터방정식에서 확인해 보자.

각속도 $\omega$로 움직인다면 위치벡터는 아래와 같다.

$$\mathbf{r}(t)=r\cos \omega t\mathbf{i}+r\sin \omega t \mathbf{j}$$

속도와 가속도 벡터는 아래와 같다.

$$\mathbf{v}(t)=-r\omega\sin \omega t\mathbf{i}+r\omega \cos \omega t \mathbf{j}$$

$$\mathbf{a}(t)=-r\omega^2 \cos \omega t\mathbf{i}-r\omega^2 \sin \omega t \mathbf{j}$$

$$|\mathbf{v}(t)|=v=r\omega,\;\; |\mathbf{a}(t)|=a=r\omega^2$$

위에 있는 식 $\displaystyle{a=\frac{v^2}{r}}$이 성립함을 간단하게 알 수 있다. 이처럼 각속도가 일정 $\omega$하면 가속도는 구심력과 같은 방향이 된다. 각속도가 일정하지 않다면 조금 복잡하다.

운동을 수학으로 나타내는 방법에 관한 공부

위에 있는 연결고리를 참고하면 된다.

$$\mathbf{a}=a_T \mathbf{T}+a_N \mathbf{N}\;\;a_T=\frac{d^2 s}{dt^2},a_N=\kappa \bigg(\frac{ds}{dt}\bigg)^2=\kappa |\mathbf{v}|^2 $$

반지름이 $\rho$인 원의 곡률 $\kappa$는 $\displaystyle{\frac{1}{\rho}}$이므로 그림과 같이 가속도가 정해진다.

나선운동

원에 감긴 실을 팽팽하게 당기면서 풀었을 때 생기는 곡선 위에 있는 점 $P(x,y)$의 위치벡터는 아래와 같다.

$$\mathbf{r}(t)=(\cos t + t \sin t)\mathbf{i}+(\sin t -t \cos t)\mathbf{j}$$

가속도를 구해보자.

$$\begin{equation}\begin{split}\mathbf{v}&=\frac{d\mathbf{r}}{dt}=(-\sin t +\sin t + t \cos t)\mathbf{i}+(\cos t - \cos t + \sin t)\mathbf{j}\\&=(t \cos t)\mathbf{i}+(t\sin t )\mathbf{j}\\|\mathbf{v}|&=\sqrt{t^2 \cos^2 t +t^2 \sin^2 t}=t\\a_T&=\frac{d}{dt}|\mathbf{v}|=1\\\mathbf{a}&=\frac{d\mathbf{v}}{dt}=(\cos t-t \sin t)\mathbf{i}+(\sin t+ t\cos t )\mathbf{j}\\|\mathbf{a}|^2&=t^2 +1\\a_N&=\sqrt{|\mathbf{a}|^2 -a_T^2}=\sqrt{(t^2 +1)-1}=t\end{split}\end{equation}$$

$$\therefore \mathbf{a}=\mathbf{T}+t\mathbf{N}$$

 

공부를 할수록 벡터로 표현하는 즐거움을 알겠다.