운동을 수학으로 나타내는 방법에 관한 공부
수학이야기/Calculus 2019. 10. 11. 12:00처음에는 아무것도 보이지 않는다. 그리스인이 말한 '카오스'나 노자가 말한 '공'이다. 무엇인지는 모르는 뭔가가 움직임을 만든다. 보이지 않던 것이 보이기 시작한다. 여전히 다음 순간 어디로 어떻게 움직일까 전혀 알 수 없다. 무질서한 움직임을 파고들면 질서가 보인다. 비로소 우리는 운동을 어렴풋이 파악할 수 있다.
점은 부분이 없는 것이다. 점이 움직이면 자취가 생긴다. 이 자취가 선이다. 유클리드는 선은 폭이 없는 길이로 정의했다. 점이 가만히 있으면 아무 것도 없지만 움직이면 움직인 거리가 생긴다. 기하학(Geometry)은 점, 선, 면으로 이루어진 도형의 길이와 넓이, 부피를 재는 공부다. 미적분(Calculus)은 움직임을 공부한다. 시각애 따라 움직인 거리를 나타내기 위해 함수가 등장한다. 여기에 방향까지 생각하면 제법 아름다운 수학이 된다. 미적분과 기하가 만나 미분 기하(Differential Geometry)를 이룬다. 이제 미분기하를 맛보기로 하자.
직선에 놓인 점의 운동
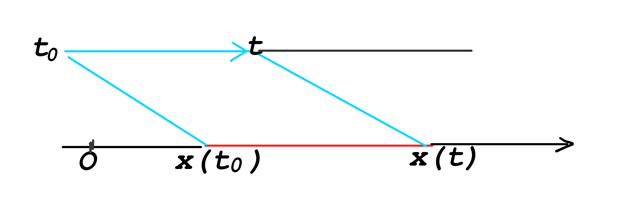
이건 아주 간단하다. 방향이 오른쪽/왼쪽만 있기 때문이다. 시각 $t$에서 점 $P$ 위치 $x$를 $x(t)$로 나타내면 된다. 오른쪽은 $x>0$, 왼쪽은 $x<0$으로 생각하면 끝이다.
평면에 놓인 점의 운동
이 운동을 나타내는 법은 간단치 않다. 따라서 크기와 함께 방향까지 나타내는 벡터가 필요하다. 위치벡터 $\overrightarrow{OP}$는 성분 표시로 $\mathbf{r}(t)=(x(t),y(t))$로 나타내자.

공간에 놓인 점의 운동
이 운동을 나타내는 법은 더 복잡하다. 위치벡터 $\overrightarrow{OP}$는 성분 표시로 $\mathbf{r}(t)=(x(t),y(t),z(t))$로 나타내자.

여기서 공간에 있는 점의 운동을 공간 곡선으로 자세하게 공부해 보자.
참고 굵은 문자 $\mathbf{r}$로 적은 것은 벡터를 가는 문자 $r$로 적은 것은 스칼라를 나타낸다. 벡터를 성분으로 표시할 때 구별을 위해 아래와 같이 $(\;)$가 아닌 $<\;>$를 쓰기도 한다.

공간 곡선은 $\mathbf{r}(t)=<f(t),g(t),h(t)>$와 같이 구간 $I$에 있는 실수에 벡터가 함숫값인 함수이므로 벡터값 함수(Vector-valued function) 또는 벡터 함수(Vector function)로 부른다. $f(t),g(t),h(t)$와 같이 성분을 나타내는 실숫값 함수(Real-valued function)은 스칼라 함수로 부른다. 기본 단위벡터 $\mathbf{i},\mathbf{j},\mathbf{k}$로 표현해도 같은 것임은 알고 있을 것이다.
$$\mathbf{r}(t)=<f(t),g(t),h(t)>=f(t)\mathbf{i}+g(t)\mathbf{j}+h(t)\mathbf{k}$$
벡터함수의 미분
이제 벡터함수를 미분해 보자.

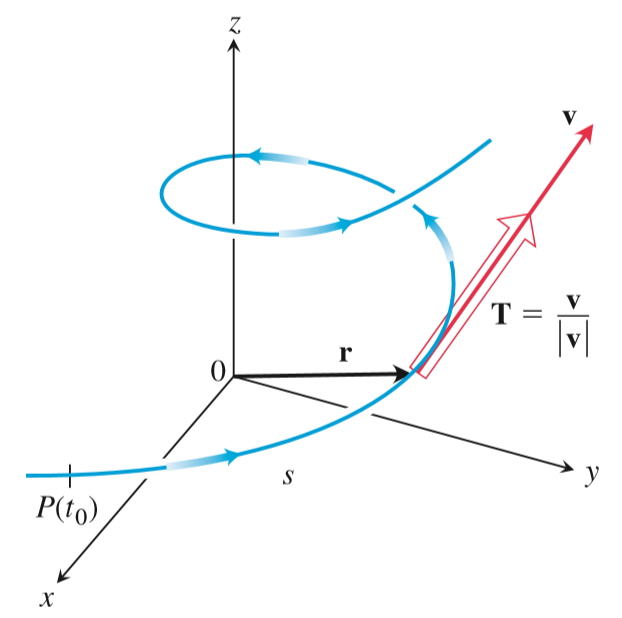
그림에서 $\Delta x \rightarrow 0$일 때, 점 $Q$는 점 $P$로 한없이 가까워진다. 따라서 극한은 접선벡터가 된다.
$$\begin{equation}\begin{split}\mathbf{r}^{\prime}(t)&=\lim_{\Delta t \rightarrow 0}\frac{\mathbf{r}(t+\Delta t)-\mathbf{r}(t)}{\Delta t}\\&=\bigg[\lim_{\Delta t \rightarrow 0}\frac{f(t+\Delta t)-f(t)}{\Delta t}\bigg]\mathbf{i}+\bigg[\lim_{\Delta t \rightarrow 0}\frac{g(t+\Delta t)-g(t)}{\Delta t}\bigg]\mathbf{j}+\bigg[\lim_{\Delta t \rightarrow 0}\frac{h(t+\Delta t)-h(t)}{\Delta t}\bigg]\mathbf{k}\\&=\bigg[\frac{d f}{d t}\bigg]\mathbf{i}+\bigg[\frac{d g}{d t}\bigg]\mathbf{j}+\bigg[\frac{d h}{d t}\bigg]+\mathbf{k}\end{split}\end{equation}$$
접선벡터는 속도(velocity)벡터로 부르자. 즉, $\displaystyle{\mathbf{v}=\frac{d \mathbf{r}}{d t}}$이다.
이 속도벡터의 크기 $|\mathbf{v}|$는 속력(speed)이다. 속력을 아래와 같이 적분하면 $t=a$부터 $t=b$까지 곡선의 길이 $L$을 구할 수 있다.
$$L=\int_{a}^{b}|\mathbf{v}(t)|dt=\int_{a}^{b}\sqrt{\bigg(\frac{d f}{d t}\bigg)^2 +\bigg(\frac{d g}{d t}\bigg)^2+\bigg(\frac{d h}{d t}\bigg)^2}d t$$
이때 곡선의 길이를 구하는 함수 $s(t)$를 아래와 같이 정의할 수 있다.
$$s(t)=\int_{t_0}^{t} \bigg|\frac{d \mathbf{r}(\tau)}{d \tau}\bigg|d \tau$$
단위 접선벡터(Unit Tangent Vector)
이제 주어진 곡선을 변수 $s$를 매개변수로 나타내서 $s$의 함수로 만들 수 있다.
$s=s(t)$이므로 $t=s^{-1}(s)$이다. 따라서 $\mathbf{r}(t)=\mathbf{r}(s^{-1}(s))$이다.
보기 주어진 곡선 $\mathbf{r}(t)=(\cos t)\mathbf{i}+(\sin t)\mathbf{j} +t \mathbf{k}$가 있다.
먼저 $t_0=0$라고 할 때, 곡선의 길이를 구해보자.
$$\mathbf{r}^{\prime}(t)=(-\sin t)\mathbf{i}+(\cos t)\mathbf{j} + \mathbf{k}$$
$$s(t)=\int_{0}^{t} \bigg|\frac{d \mathbf{r}(\tau)}{d \tau}\bigg|d \tau=\int_{0}^{t}\sqrt {2}d \tau=\sqrt{2} t$$
$t=s/\sqrt{2}$이다.
$$\mathbf{r}(t(s))=\bigg(\cos \frac{s}{\sqrt{2}}\bigg)\mathbf{i}+\bigg(\sin \frac{s}{\sqrt{2}}\bigg)\mathbf{j} + \frac{s}{\sqrt{2}} \mathbf{k} $$
이렇게 매개변수를 바꾸는 것을 곡선의 재매개변수화로 부른다. 변수 $s$로 재매개변수화하면 다루기 쉬운 함수를 얻을 수 있지만 보기처럼 간단한 함수가 아니라면 재매개변수화가 쉽지는 않다. 재매개변수화된 곡선을 $s$에 대해 미분하면 크기가 1인 단위벡터를 얻게 되는데 이 벡터를 단위 접선벡터(Unit tangent vector:$T$)라 부른다. 아래와 같이 구하면 된다. 참고로 벡터함수를 다시 매개화하는 변수 $s$에 대해 미분함을 위에 점을 찍어서 $\dot{\mathbf{r}}$로 표기하기도 한다.
$$T=\frac{d \mathbf{r}}{d s}=\frac{d \mathbf{r}}{ d t} \frac{d t}{d s}=\frac{\mathbf{v}}{|\mathbf{v}|}$$
곡률과 법선벡터(Curvature and normal vectors of a Curve )
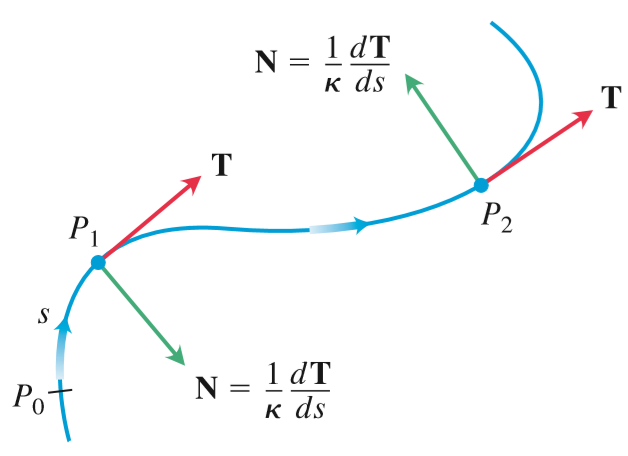
단위 접선벡터는 크기가 모두 1이므로 $\Delta s$에 대한 $\Delta T$는 곡선의 방향이 변화는 양을 나타낸다. 따라서 $\displaystyle{\frac{d T}{d s}}$ 벡터 의 크기는 곡선이 휜 정도를 보여준다. 이것을 곡률(Curvature: $\kappa$)이라고 한다.
$$ \kappa=\bigg| \frac{d T}{d s}\bigg|=\bigg| \frac{d T}{d t}\frac{d t}{d s}\bigg|=\frac{1}{|d s/ dt|}\bigg| \frac{d T}{d t}\bigg|=\frac{1}{|\mathbf{v}|}\bigg| \frac{d T}{d t}\bigg|$$
$T\cdot T=1$이므로 미분하면 $(dT/ds) \cdot T+T \cdot(dT/ds)=0$이다. 따라서 두 벡터 $dT/ds$와 $T$는 서로 수직이다. 벡터 $dT/ds$와 같은 방향(법선방향)인 단위 벡터를 생각하자. 아래와 같이 단위 법선벡터(Unit normal vector) $N$를 정의한다.
정의 곡률 $\kappa\not=0$인 매끄러운 곡선에서
$$N=\frac{1}{\kappa}\frac{d T}{ds}$$
$dt/ds>0$라고 생각하면 아래와 같이 계산할 수 있다.
$$N=\frac{d T/ds}{|d T/ds|}=\frac{(d T/d t)(dt /ds)}{|dT/dt||dt/ds|}=\frac{d T/dt}{|d T/dt|}$$
이중법선벡터와 뒤틀림(Binormal vector and tortion)
공간 곡선은 휘어지기도 하지만 뒤틀리기도 한다. 곡선의 뒤틀림 정도를 나타내는 방법을 알아보자.
먼저 아래와 같이 단위 접선벡터와 법선벡의 외적을 이중법선벡터(binormal vector)라 한다.
$$B=T\times N$$
세 벡터 $T,N,B$로 만든 오른손-법칙을 따르는 틀을 프레네이 프레임(Frenet frame) 또는 TNB frame이라고 부른다. 이를 이용하면 공간 곡선 위에 있는 점의 운동을 쉽게 파악할 수 있다.
먼저 속도와 가속도를 살펴보자.
$$\begin{equation}\begin{split}\mathbf{v}&=\frac{d\mathbf{r}}{dt}=\frac{d\mathbf{r}}{ds}\frac{ds}{dt}=T \frac{ds}{dt}\\\mathbf{a}&=\frac{d\mathbf{v}}{dt}=\frac{d}{dt}\bigg(T \frac{ds}{dt}\bigg)=\frac{d^2 s}{dt^2} T+\frac{ds}{dt}\frac{d T}{dt} \\&=\frac{d^2 s}{dt^2} T+\frac{ds}{dt}\bigg(\frac{d T}{ds}\frac{ds}{dt}\bigg)\\& =\frac{d^2 s}{dt^2} T+\frac{ds}{dt}\bigg(\kappa N\frac{ds}{dt}\bigg) \\&=\frac{d^2 s}{dt^2} T+\kappa \bigg(\frac{ds}{dt}\bigg)^2 N \end{split}\end{equation}$$
아래에 있는 그림처럼 가속도 벡터 $\mathbf{a}$는 두 벡터 $T,N$의 선형결합으로 나타나므로 두 벡터와 같은 평면에 있음을 알 수 있다.
$$\mathbf{a}=a_T \mathbf{T}+a_N \mathbf{N}\;\;a_T=\frac{d^2 s}{dt^2},a_N=\kappa \bigg(\frac{ds}{dt}\bigg)^2=\kappa |\mathbf{v}|^2 $$
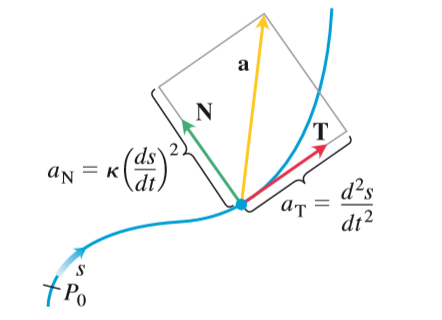
가속도 벡터 $\mathbf{a}$와 $a_T$는 쉽게 계산할 수 있으므로 곡률벡터 $N$를 구하지 않고 $a_N$을 계산할 수 있다.
$$a_N=\sqrt{\mathbf{a}\cdot\mathbf{a}-a_T^2}$$
이래와 같이 곡률과 마찬가지로 $\Delta s$에 대한 $\Delta B$의 변화는 곡선이 뒤틀림($\tau$) 정도를 나타낸다.
$$\tau=\bigg|\frac{d B}{ds}\bigg|$$
$$\frac{d B}{ds}=\frac{d T\times N}{ds}=\frac{d T}{ds}\times N+T\times \frac{d N}{ds}$$
여기서 $N$은 $dT/ds$와 같은 방향이므로 외적은 $0$이다.
$$\frac{d B}{ds}=0+T\times \frac{d N}{ds}$$
$dB/ds$는 $T$와 수직이다. 또한 $B$와도 수직이므로 $N$과 평행하다. 이것을 아래처럼 적당한 상수로 나타내자.
$$\frac{d B}{ds}=-\tau N$$
정의 $B=T\times B$일 때 매끄러운 곡선의 뒤틀림 함수는 아래와 같다. $$\tau=-\frac{d B}{ds}N$$
$N=B\times T$를 미분하면
$$\frac {d \mathbf {N} }{ds}=\frac {d\mathbf {B} }{ds}\times \mathbf{T}+\mathbf{B}\times \frac {d\mathbf {T}}{ds} =-\tau\mathbf{N} \times \mathbf{T}+\kappa \mathbf{B} \times \mathbf{N}=-\kappa \mathbf {T} +\tau \mathbf {B}$$
세 벡터 $T,N,B$ 사이의 관계는 아래와 같다.
$$\displaystyle {\begin{aligned}{\dfrac {d\mathbf {T} }{ds}}&=\kappa \mathbf {N} \\{\dfrac {d\mathbf {N} }{ds}}&=-\kappa \mathbf {T} +\tau \mathbf {B} \\{\dfrac {d\mathbf {B} }{ds}}&=-\tau \mathbf {N} \end{aligned}}$$
위에 적은대로 곡선을 변수 $s$로 재매개변수화하는 일은 매우 어렵다. 따라서 변수 $t$에 대한 함수로 표현된 식에서 곡률을 구하는 방법을 알아두어야 한다.
$$\begin{aligned} \mathbf{v} \times \mathbf{a} & =\bigg( \frac{d s}{d t} \mathbf {T} \bigg) \times \bigg[ \frac{d^2 s}{d t^2} \mathbf{T}+\kappa \bigg( \frac{ds}{dt} \bigg)^2 \mathbf{N} \bigg]\\&=\bigg( \frac{ds}{dt} \frac{d^2 s}{dt^2} \bigg) (\mathbf{T} \times \mathbf{T})+\kappa \bigg( \frac{ds}{dt} \bigg)^3(\mathbf{T} \times \mathbf{N} )\\&=\kappa \bigg( \frac{ds}{dt} \bigg)^3 \mathbf {B} \end{aligned}$$
$$|\mathbf{v} \times \mathbf{a}|=\kappa \bigg| \frac{ds}{dt} \bigg|^3 |\mathbf {B}|=\kappa |\mathbf{v}|^3 $$
$$\kappa=\frac{|\mathbf{v}\times\mathbf{a}|}{|\mathbf{v}|^3}$$
곡선 $\mathbf{r}(t)=<x(t),y(t),z(t)>$라고 할 때, 토션 $\displaystyle{\tau=-\frac{d \mathbf{B}}{d s}\cdot \mathbf{N}}$은 아래와 같이 계산한다.
$$\begin{equation}\begin{split} \dot {\mathbf{r}} &=\mathbf{T}=\frac{d\mathbf{r}}{dt}\frac{dt}{ds}=\frac{d\mathbf{r}}{dt} \frac{1}{|\mathbf{v}|} \\ \ddot {\mathbf{r}} &= \kappa\mathbf{N}=\frac{d\mathbf{T}}{ds}=\frac{d\mathbf{T}}{dt}\frac{dt}{ds}=\frac{d\mathbf{T}}{dt} \frac{1}{|\mathbf{v}|} \\&= \frac{d}{dt} \bigg( \frac{d\mathbf{r}}{dt} \frac{1}{|\mathbf{v}|} \bigg) \frac{1}{|\mathbf{v}| }= \bigg(\frac{d^2 \mathbf{r}}{dt^2} \frac{1} {|\mathbf{v}|} + \frac{d \mathbf{r}}{dt} \frac{d}{dt} \bigg( \frac{1}{|\mathbf{v}|} \bigg ) \bigg ) \frac{1}{|\mathbf{v}|} \\&= \frac{d^2 \mathbf{r}}{dt^2} \frac{1} {|\mathbf{v}|^2}+\mathbf{T} \frac{d}{dt} \bigg( \frac{1}{|\mathbf{v}|} \bigg) \\ \dddot {\mathbf{r}} &= \dot {\kappa} \mathbf{N}+\kappa (\tau \mathbf{B}-\kappa \mathbf{T}) = \frac{d}{ds} \bigg(\frac{d\mathbf{T}}{ds} \bigg) =\frac{d}{dt} \bigg(\frac{d\mathbf{T}}{dt}\frac{1}{|\mathbf{v}|} \bigg) \frac{dt}{ds} \\&=\frac{d}{dt} \bigg(\frac{d^2 \mathbf{r}}{dt^2} \frac{1} {|\mathbf{v}|^2}+\mathbf{T} \frac{d}{dt} \bigg( \frac{1}{|\mathbf{v}|} \bigg) \bigg) \frac{1}{|\mathbf{v}|} \\&= \bigg(\frac{d^3 \mathbf{r}}{dt^3} \frac{1} {|\mathbf{v}|^2} +\frac{d^2 \mathbf{r}}{dt^2} \frac{d}{dt}\bigg( \frac{1} {|\mathbf{v}|^2}\bigg) +\frac{d\mathbf{T}}{dt}\frac{d}{dt} \bigg( \frac{1}{|\mathbf{v}|}\bigg) + \mathbf{T} \frac{d^2}{dt^2} \bigg( \frac{1}{|\mathbf{v}|} \bigg) \bigg) \frac{1}{|\mathbf{v}|} \\&= \frac{d^3 \mathbf{r}}{dt^3} \frac{1} {|\mathbf{v}|^3} +\frac{d^2 \mathbf{r}}{dt^2} \frac{d}{dt}\bigg( \frac{1} {|\mathbf{v}|^2}\bigg) \frac{1}{|\mathbf{v}|} +\frac{d\mathbf{T}}{dt}\frac{d}{dt} \bigg( \frac{1}{|\mathbf{v}|}\bigg) \frac{1}{|\mathbf{v}|} + \mathbf{T} \frac{d^2}{dt^2} \bigg( \frac{1}{|\mathbf{v}|} \bigg) \frac{1}{|\mathbf{v}|}\\&= \frac{d^3 \mathbf{r}}{dt^3} \frac{1} {|\mathbf{v}|^3} +\mathbf{a} \frac{d}{dt}\bigg( \frac{1} {|\mathbf{v}|^2}\bigg) \frac{1}{|\mathbf{v}|} +\mathbf{N} \frac{d}{dt} \bigg( \frac{1}{|\mathbf{v}|}\bigg) + \mathbf{T} \frac{d^2}{dt^2} \bigg( \frac{1}{|\mathbf{v}|} \bigg) \frac{1}{|\mathbf{v}|} \end{split} \end{equation}$$
이제 토션을 구해보자. 먼저 아래와 같음을 확인하자.
$$(\dot {\mathbf{r}}\times \ddot{\mathbf{r}})\cdot \dddot{\mathbf{r}}=\kappa^2 \tau$$
여기서 $\mathbf{T}\bot\mathbf{N},\;\;\mathbf{a}\bot(\mathbf{T}\times\mathbf{N})$이므로 $\mathbf{T}\cdot \mathbf{N}=0,\;\;\mathbf{a}\cdot(\mathbf{T}\times\mathbf{N})=0$이다.
따라서 아래와 같다.
$$(\dot {\mathbf{r}}\times \ddot{\mathbf{r}})\cdot \dddot{\mathbf{r}}=\frac{(\mathbf{r}'\times \mathbf{r}'')\cdot \mathbf{r}''' }{|\mathbf{v}|^6} $$
$$\tau=\frac{det(\mathbf{r}^{\prime},\mathbf{r}^{\prime\prime},\mathbf{r}^{\prime\prime\prime})}{|\mathbf{r}^{\prime}\times \mathbf{r}^{\prime\prime}|^2}=\frac{(\mathbf{r}^{\prime}\times\mathbf{r}^{\prime\prime})\cdot\mathbf{r}^{\prime\prime\prime}}{|\mathbf{r}^{\prime}\times \mathbf{r}^{\prime\prime}|^2}$$
$$\tau =\frac { \begin{vmatrix} x'& y' &z' \\ x'' &y ''& z''\\x'''&y'''&z'''\end{vmatrix} }{|\mathbf{v} \times \mathbf{a}|^2}={\frac {x'''(y'z''-y''z')+y'''(x''z'-x'z'')+z'''(x'y''-x''y')}{(y'z''-y''z')^{2}+(x''z'-x'z'')^{2}+(x'y''-x''y')^{2}}}$$







